
§11-2等截面直杆的形常数载常数 位移法的基础是杆件分析。为此,需先研究 杆件(单跨超静定杆)杆端力和杆端位移、荷载 之间的关系。 因为是从结构中取出来的,杆件两端并不 定是真正的固定端、铰支端、滑动端、,各杆 端都可能有线位移和角位移。常见的有以下几种 单跨杆:
§ 11-2 等截面直杆的形常数和载常数 位移法的基础是杆件分析。为此,需先研究 杆件(单跨超静定杆)杆端力和杆端位移、荷载 之间的关系。 因为是从结构中取出来的,杆件两端并不一 定是真正的固定端、铰支端、滑动端、…,各杆 端都可能有线位移和角位移。常见的有以下几种 单跨杆:
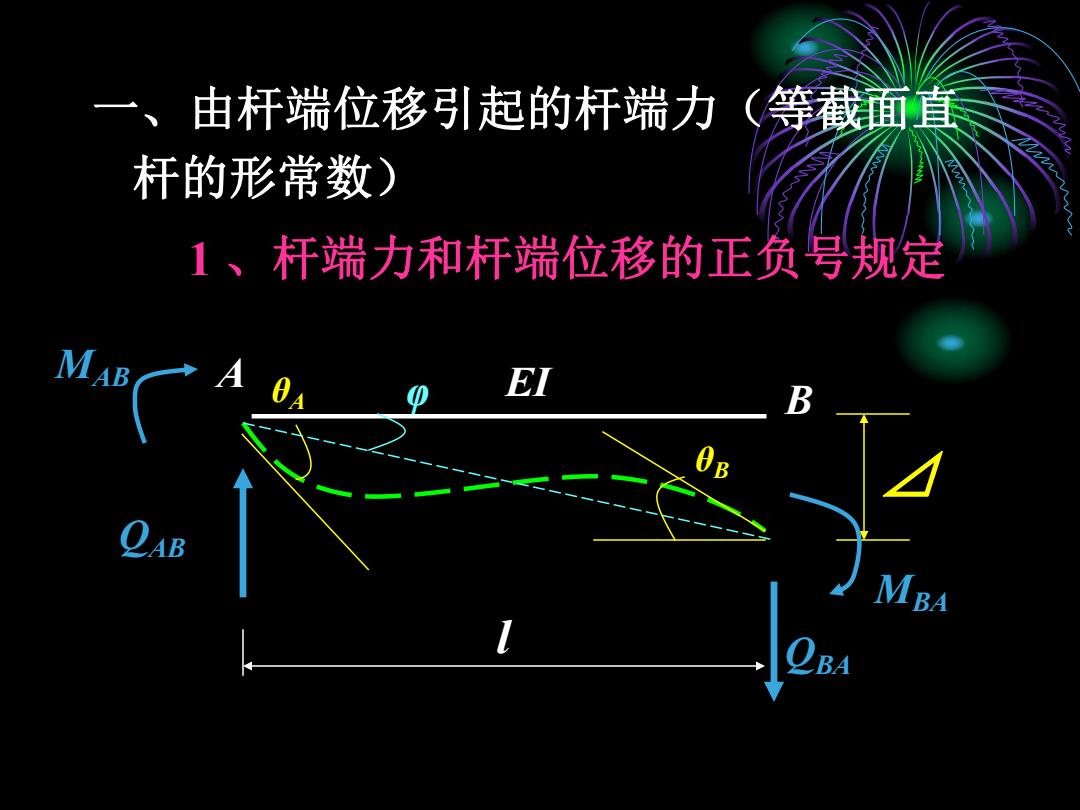
一、由杆端位移引起的杆端力(等截面直 杆的形常数) 1、杆端力和杆端位移的正负号规定 MAB EI B MBA BA
l A EI B ⊿ θA φ θB MAB QAB MBA QBA 一、由杆端位移引起的杆端力(等截面直 杆的形常数) 1 、杆端力和杆端位移的正负号规定
MAB EI AB MBA BA (1)杆端转角04、0g, 弦转角p=几 均以顺时针方向转动为正 (2)杆端弯矩M4B、MB4规定对杆端以 顺时针方向为正。 (3) 杆端剪力Q4B、QB1的正方向规定 同前
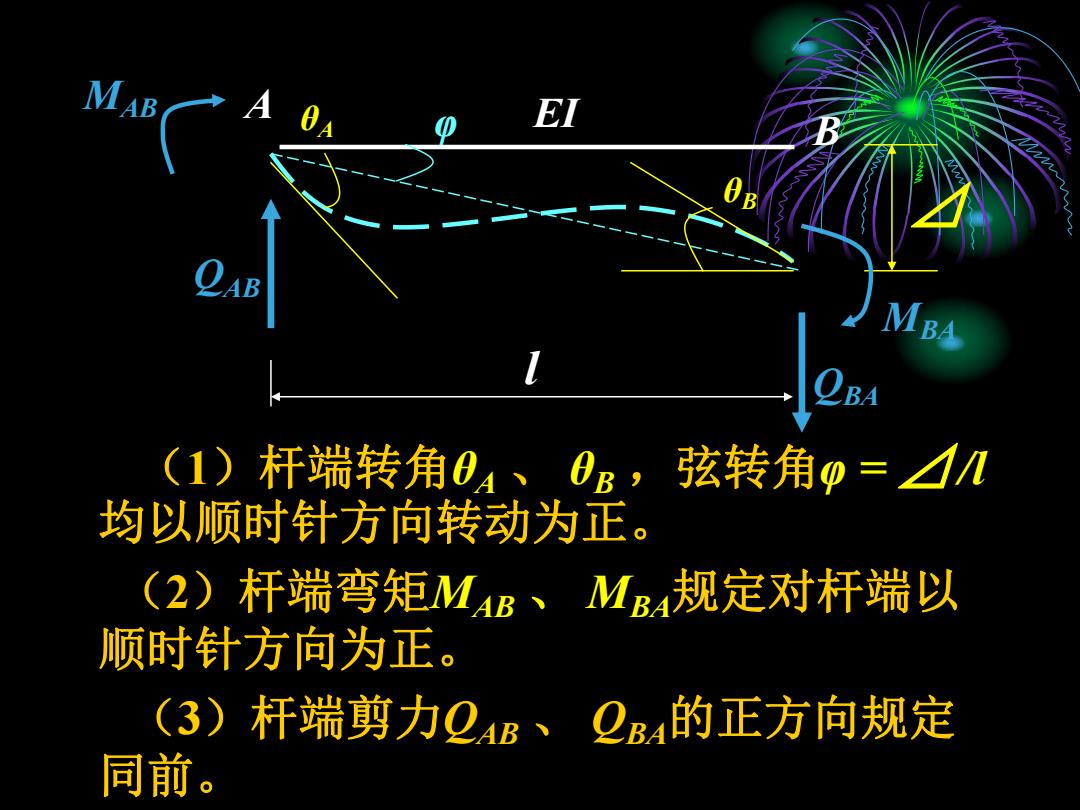
(1)杆端转角θA 、 θB ,弦转角φ = ⊿ /l 均以顺时针方向转动为正。 (2)杆端弯矩MAB 、 MBA规定对杆端以 顺时针方向为正。 (3)杆端剪力QAB 、 QBA的正方向规定 同前。 l A EI B ⊿ θA φ θB MAB QAB MBA QBA

注意:杆端弯矩的正负号规则与通常关手 弯矩的正负号规则不同。 (1)此处规则是针对杆端弯矩,而不是针 对杆中任一截面的弯矩。 (2)当取杆件(或取结点)为隔离体时, 杆端弯矩是隔离体上的外力,建立隔离体平衡 方程时,力矩一律以顺时针(或逆时针)转向 为正。 因此,这里的规则是把杆端弯矩视为外力, 为了便于建立平衡方程而规定的。 杆端弯矩有双重身份:既是杆件的内力又 是隔离体外力
注意:杆端弯矩的正负号规则与通常关于 弯矩的正负号规则不同。 (1)此处规则是针对杆端弯矩,而不是针 对杆中任一截面的弯矩。 ( 2 )当取杆件(或取结点)为隔离体时, 杆端弯矩是隔离体上的外力,建立隔离体平衡 方程时,力矩一律以顺时针(或逆时针)转向 为正。 杆端弯矩有双重身份:既是杆件的内力又 是隔离体外力。 因此,这里的规则是把杆端弯矩视为外力, 为了便于建立平衡方程而规定的

当杆端位移等于1时,所得的杆端力称 为等截面直杆的刚度系数。因刚度系数只与 杆件材料性质、尺寸及截面的几何形状有关 故也称为形常数。 2、当A端作为固定端,有角位移0=1时的 形常数 见教材P2 (1)B端为固定支座时 (2)B端为铰支座时 (3)B端为滑动支座时
当杆端位移等于1时,所得的杆端力称 为等截面直杆的刚度系数。因刚度系数只与 杆件材料性质、尺寸及截面的几何形状有关, 故也称为形常数。 2、当A端作为固定端,有角位移θA=1时的 形常数 见教材P2 (1)B端为固定支座时 (2)B端为铰支座时 (3)B端为滑动支座时