
表 5-2 氨基酸在水中的溶解度 氨基酸 溶解度(g/L) 氨基酸 溶解度(g/L) 丙氨酸 167.2 亮氨酸 21.7 精氨酸 855.6 赖氨酸 739.0 天冬酰胺 28.5 蛋氨酸 56.2 天冬氨酸 5.0 苯丙氨酸 27.6 半胱氨酸 - 脯氨酸 1620.0 谷胺酰胺 7.2(37℃) 丝氨酸 422.0 谷氨酸 甘氨酸 8.5 249.9 苏氨酸 色氨酸 13.2 13.6 组氨酸 - 酪氨酸 0.4 异亮氨酸 34.5 缬氨酸 58.1 除上述 20 种氨基酸外,在动物、植物或微生物的细胞中还存在 150 种以上 游离或结合的氨基酸,其中多数是重要的代谢中间产物(或前体),或者是参与 传递神经冲动的化学介体。在某些抗生素中还存在 D 构型氨基酸。 2. 氨基酸的酸碱性质 氨基酸的离子化能力在生物学上是非常重要的,这种性质可用来进行定量分 析。另外,氨基酸的一些性质(熔点、溶解度、偶极矩和在水溶液中的介电常数) 都是由于在水溶液中的电荷分布不均匀而产生的。因而,所有氨基酸在接近中性 pH 的水溶液中主要以两性离子(zwitterion),亦称偶极离子(dipolarion)的 形式存在。 R C O O N H 3 + C H - 由于,氨基酸同时含有羧基(酸性)和氨基(碱性),因此,当氨基酸溶解 于水时,可表现为酸的行为: R C O O N H 2 R C O O H + + C H - N H 3 + C H - 又可表现出碱的性质: H + R C O O N H 3 + C H + R C O O + H N H 3 C H - 因此,是一类两性电解质。以最简单的甘氨酸(Gly)为例,在溶液中由于受 pH
表 5-2 氨基酸在水中的溶解度 氨基酸 溶解度(g/L) 氨基酸 溶解度(g/L) 丙氨酸 167.2 亮氨酸 21.7 精氨酸 855.6 赖氨酸 739.0 天冬酰胺 28.5 蛋氨酸 56.2 天冬氨酸 5.0 苯丙氨酸 27.6 半胱氨酸 - 脯氨酸 1620.0 谷胺酰胺 7.2(37℃) 丝氨酸 422.0 谷氨酸 甘氨酸 8.5 249.9 苏氨酸 色氨酸 13.2 13.6 组氨酸 - 酪氨酸 0.4 异亮氨酸 34.5 缬氨酸 58.1 除上述 20 种氨基酸外,在动物、植物或微生物的细胞中还存在 150 种以上 游离或结合的氨基酸,其中多数是重要的代谢中间产物(或前体),或者是参与 传递神经冲动的化学介体。在某些抗生素中还存在 D 构型氨基酸。 2. 氨基酸的酸碱性质 氨基酸的离子化能力在生物学上是非常重要的,这种性质可用来进行定量分 析。另外,氨基酸的一些性质(熔点、溶解度、偶极矩和在水溶液中的介电常数) 都是由于在水溶液中的电荷分布不均匀而产生的。因而,所有氨基酸在接近中性 pH 的水溶液中主要以两性离子(zwitterion),亦称偶极离子(dipolarion)的 形式存在。 R C O O N H 3 + C H - 由于,氨基酸同时含有羧基(酸性)和氨基(碱性),因此,当氨基酸溶解 于水时,可表现为酸的行为: R C O O N H 2 R C O O H + + C H - N H 3 + C H - 又可表现出碱的性质: H + R C O O N H 3 + C H + R C O O + H N H 3 C H - 因此,是一类两性电解质。以最简单的甘氨酸(Gly)为例,在溶液中由于受 pH
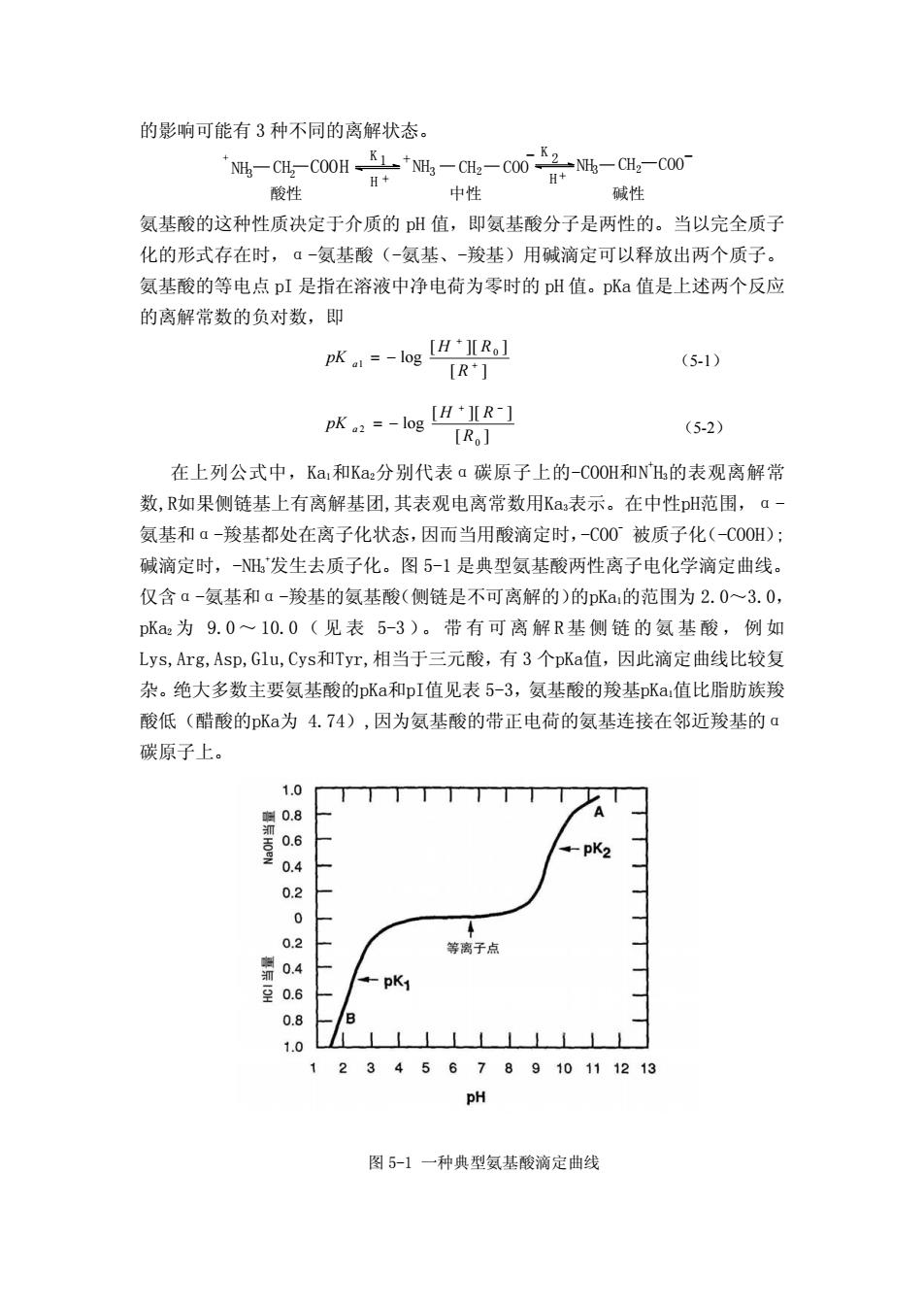
的影响可能有 3 种不同的离解状态。 酸性 中性 碱性 C H C O O 2 + N H H C H C O O 2 + N H - C H C O O 2 N H - 3 3 3 K K 1 + + 2 H H 氨基酸的这种性质决定于介质的 pH 值,即氨基酸分子是两性的。当以完全质子 化的形式存在时,α-氨基酸(-氨基、-羧基)用碱滴定可以释放出两个质子。 氨基酸的等电点 pI 是指在溶液中净电荷为零时的 pH 值。pKa 值是上述两个反应 的离解常数的负对数,即 在上列公式中,Ka1和Ka2分别代表α碳原子上的-COOH和N + H3的表观离解常 数,R如果侧链基上有离解基团,其表观电离常数用Ka3表示。在中性pH范围,α- 氨基和α-羧基都处在离子化状态,因而当用酸滴定时,-COO- 被质子化(-COOH); 碱滴定时,-NH3 + 发生去质子化。图 5-1 是典型氨基酸两性离子电化学滴定曲线。 仅含α-氨基和α-羧基的氨基酸(侧链是不可离解的)的pKa1的范围为 2.0~3.0, pKa2 为 9.0 ~ 10.0 ( 见 表 5-3 )。带有可离解R基侧链的氨基酸,例如 Lys,Arg,Asp,Glu,Cys和Tyr,相当于三元酸,有 3 个pKa值,因此滴定曲线比较复 杂。绝大多数主要氨基酸的pKa和pI值见表 5-3,氨基酸的羧基pKa1值比脂肪族羧 酸低(醋酸的pKa为 4.74),因为氨基酸的带正电荷的氨基连接在邻近羧基的α 碳原子上。 图 5-1 一种典型氨基酸滴定曲线 [ ] [ ][ ] log + = − R pK 0 1 + R H a (5-1) [ ] [ ][ ] log 0 2 R H R pK a + − = − (5-2)
的影响可能有 3 种不同的离解状态。 酸性 中性 碱性 C H C O O 2 + N H H C H C O O 2 + N H - C H C O O 2 N H - 3 3 3 K K 1 + + 2 H H 氨基酸的这种性质决定于介质的 pH 值,即氨基酸分子是两性的。当以完全质子 化的形式存在时,α-氨基酸(-氨基、-羧基)用碱滴定可以释放出两个质子。 氨基酸的等电点 pI 是指在溶液中净电荷为零时的 pH 值。pKa 值是上述两个反应 的离解常数的负对数,即 在上列公式中,Ka1和Ka2分别代表α碳原子上的-COOH和N + H3的表观离解常 数,R如果侧链基上有离解基团,其表观电离常数用Ka3表示。在中性pH范围,α- 氨基和α-羧基都处在离子化状态,因而当用酸滴定时,-COO- 被质子化(-COOH); 碱滴定时,-NH3 + 发生去质子化。图 5-1 是典型氨基酸两性离子电化学滴定曲线。 仅含α-氨基和α-羧基的氨基酸(侧链是不可离解的)的pKa1的范围为 2.0~3.0, pKa2 为 9.0 ~ 10.0 ( 见 表 5-3 )。带有可离解R基侧链的氨基酸,例如 Lys,Arg,Asp,Glu,Cys和Tyr,相当于三元酸,有 3 个pKa值,因此滴定曲线比较复 杂。绝大多数主要氨基酸的pKa和pI值见表 5-3,氨基酸的羧基pKa1值比脂肪族羧 酸低(醋酸的pKa为 4.74),因为氨基酸的带正电荷的氨基连接在邻近羧基的α 碳原子上。 图 5-1 一种典型氨基酸滴定曲线 [ ] [ ][ ] log + = − R pK 0 1 + R H a (5-1) [ ] [ ][ ] log 0 2 R H R pK a + − = − (5-2)

pKa是表观离解平衡常数的负对数,pI(等电点)是电中性状态(净电荷为 零)时的pH值。根据下列等式,利用氨基酸的pKa1,pKa2和pKa3值可估算等电点值: 不带电荷侧链的氨基酸 pI=(pKa1+pKa2)/2 酸性氨基酸 pI=(pKa1+pKa3)/2 碱性氨基酸 pI=(pKa2+pKa3)/2 在等电点以上的任何 pH 值,氨基酸带净负电荷,并因此在电场中将向正极 移动。在低于等电点的任一 pH 值,氨基酸带有净正电荷,在电场中将向负极移 动。在一定 pH 范围内,氨基酸溶液的 pH 离等电点愈远,氨基酸携带的净电荷愈 多。 在蛋白质分子中,氨基酸的α-COOH是通过酰胺键与邻近氨基酸的α-NH2相 结合,可以离解的基团只能是N-端氨基酸残基的氨基,C-端氨基酸残基的羧基和 侧链上的可离解基团。因此,蛋白质中这些可离解基团的pKa值不同于相应的游 离氨基酸。蛋白质中的谷氨酸和天冬氨酸的酸性侧链基团的pKa3值大于相应的游 离氨基酸的pKa3值,而碱性侧链的pKa3值则小于相应游离氨基酸的pKa3值。 根据 Henderson-Hasselbach 公式 [ ] [ ] 共轭酸 共轭碱 pH = pKa + log (5-3) 可以计算出任一 pH 条件下一种氨基酸的各种离子的离子化程度,并求出总 的负电荷和正电荷之和,从而可计算出某一蛋白质在此 pH 时的净电荷。 3.氨基酸的疏水性 蛋白质在水中的溶解度同氨基酸侧链的极性基团(带电荷或不带电荷)和非 极性(疏水)基团的分布状态有关,而且蛋白质和肽的结构、溶解性和结合脂肪 的能力等许多物理化学性质,都受到组成氨基酸疏水性的影响。氨基酸以及肽和 蛋白质的疏水程度可以根据氨基酸在水和弱极性溶剂例如乙醇中的相对溶解度 来确定,将 1mol 氨基酸从水溶液中转移到乙醇溶液中,自由能的变化(即转移自 由能)可从下式计算(忽略活度系数): ∆ ∆ Gt 0 = -RTlnS乙醇/S水 (5-4) 式中,S乙醇和S水分别表示氨基酸在乙醇和水中的溶解度(mol/L)。假若氨基酸有 多个基团,则∆ ∆ Gt 0 是氨基酸中各个基团的加合函数。 ∆ ∆ Gt 0 =Σ∆ Gt 0 ´ (5-5) 例如苯丙氨酸,从水向乙醇中转移的自由能可以分为两个部分,一部分是苄 基,另一部分是氨基和羧基
pKa是表观离解平衡常数的负对数,pI(等电点)是电中性状态(净电荷为 零)时的pH值。根据下列等式,利用氨基酸的pKa1,pKa2和pKa3值可估算等电点值: 不带电荷侧链的氨基酸 pI=(pKa1+pKa2)/2 酸性氨基酸 pI=(pKa1+pKa3)/2 碱性氨基酸 pI=(pKa2+pKa3)/2 在等电点以上的任何 pH 值,氨基酸带净负电荷,并因此在电场中将向正极 移动。在低于等电点的任一 pH 值,氨基酸带有净正电荷,在电场中将向负极移 动。在一定 pH 范围内,氨基酸溶液的 pH 离等电点愈远,氨基酸携带的净电荷愈 多。 在蛋白质分子中,氨基酸的α-COOH是通过酰胺键与邻近氨基酸的α-NH2相 结合,可以离解的基团只能是N-端氨基酸残基的氨基,C-端氨基酸残基的羧基和 侧链上的可离解基团。因此,蛋白质中这些可离解基团的pKa值不同于相应的游 离氨基酸。蛋白质中的谷氨酸和天冬氨酸的酸性侧链基团的pKa3值大于相应的游 离氨基酸的pKa3值,而碱性侧链的pKa3值则小于相应游离氨基酸的pKa3值。 根据 Henderson-Hasselbach 公式 [ ] [ ] 共轭酸 共轭碱 pH = pKa + log (5-3) 可以计算出任一 pH 条件下一种氨基酸的各种离子的离子化程度,并求出总 的负电荷和正电荷之和,从而可计算出某一蛋白质在此 pH 时的净电荷。 3.氨基酸的疏水性 蛋白质在水中的溶解度同氨基酸侧链的极性基团(带电荷或不带电荷)和非 极性(疏水)基团的分布状态有关,而且蛋白质和肽的结构、溶解性和结合脂肪 的能力等许多物理化学性质,都受到组成氨基酸疏水性的影响。氨基酸以及肽和 蛋白质的疏水程度可以根据氨基酸在水和弱极性溶剂例如乙醇中的相对溶解度 来确定,将 1mol 氨基酸从水溶液中转移到乙醇溶液中,自由能的变化(即转移自 由能)可从下式计算(忽略活度系数): ∆ ∆ Gt 0 = -RTlnS乙醇/S水 (5-4) 式中,S乙醇和S水分别表示氨基酸在乙醇和水中的溶解度(mol/L)。假若氨基酸有 多个基团,则∆ ∆ Gt 0 是氨基酸中各个基团的加合函数。 ∆ ∆ Gt 0 =Σ∆ Gt 0 ´ (5-5) 例如苯丙氨酸,从水向乙醇中转移的自由能可以分为两个部分,一部分是苄 基,另一部分是氨基和羧基
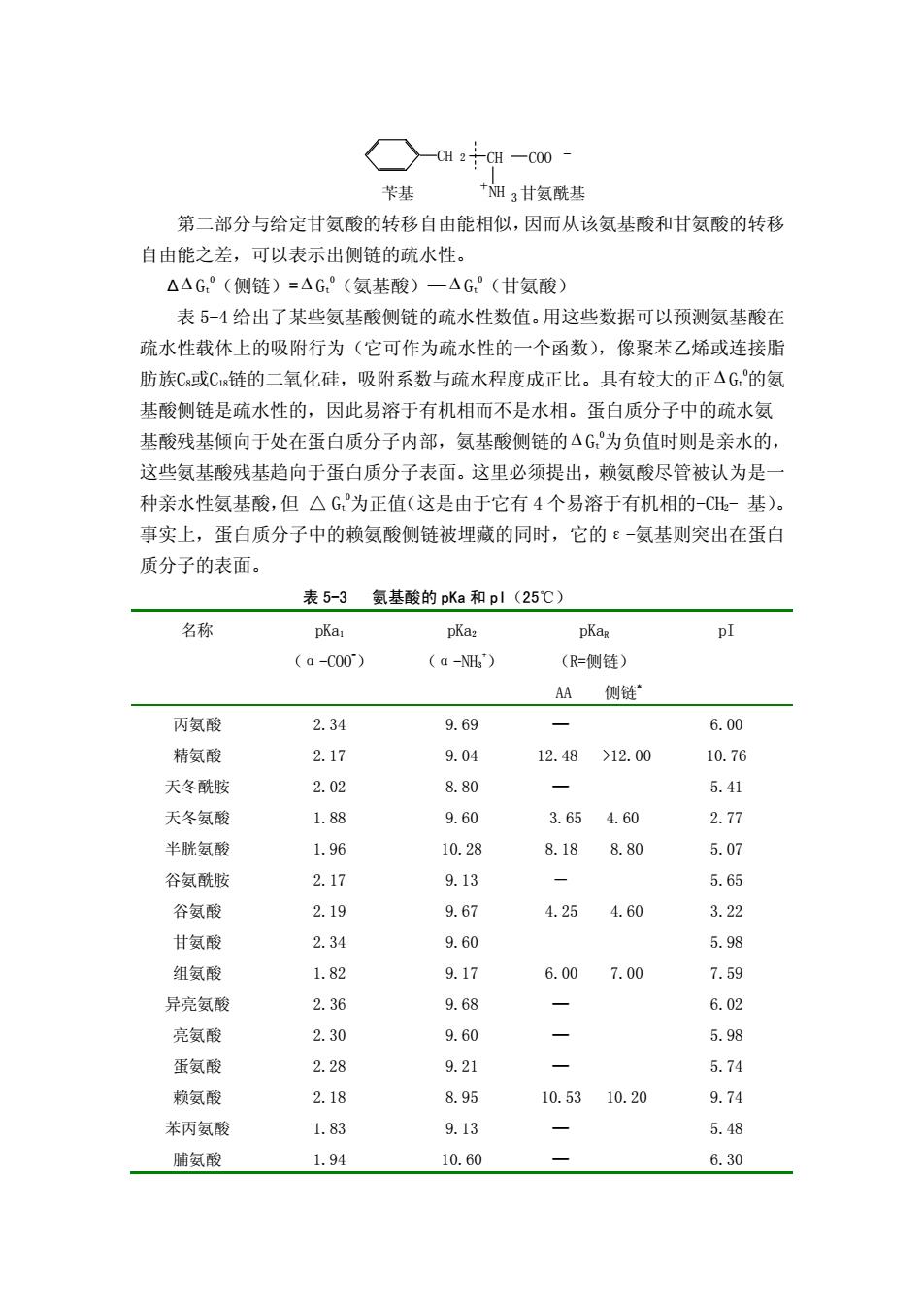
苄基 甘氨酰基 3 C H - + N H C H 2 C O O 第二部分与给定甘氨酸的转移自由能相似,因而从该氨基酸和甘氨酸的转移 自由能之差,可以表示出侧链的疏水性。 ∆ ∆ Gt 0 (侧链)= ∆ Gt 0 (氨基酸)—∆ Gt 0 (甘氨酸) 表 5-4 给出了某些氨基酸侧链的疏水性数值。用这些数据可以预测氨基酸在 疏水性载体上的吸附行为(它可作为疏水性的一个函数),像聚苯乙烯或连接脂 肪族C8或C18链的二氧化硅,吸附系数与疏水程度成正比。具有较大的正∆ Gt 0 的氨 基酸侧链是疏水性的,因此易溶于有机相而不是水相。蛋白质分子中的疏水氨 基酸残基倾向于处在蛋白质分子内部,氨基酸侧链的∆ Gt 0 为负值时则是亲水的, 这些氨基酸残基趋向于蛋白质分子表面。这里必须提出,赖氨酸尽管被认为是一 种亲水性氨基酸,但 △ Gt 0 为正值(这是由于它有 4 个易溶于有机相的-CH2- 基)。 事实上,蛋白质分子中的赖氨酸侧链被埋藏的同时,它的ε-氨基则突出在蛋白 质分子的表面。 表 5-3 氨基酸的 pKa 和 pI(25℃) 名称 pKa1 (α-COO- ) pKa2 (α-NH3 + ) pKaR (R=侧链) AA 侧链* pI 丙氨酸 2.34 9.69 — 6.00 精氨酸 2.17 9.04 12.48 >12.00 10.76 天冬酰胺 2.02 8.80 — 5.41 天冬氨酸 1.88 9.60 3.65 4.60 2.77 半胱氨酸 1.96 10.28 8.18 8.80 5.07 谷氨酰胺 2.17 9.13 - 5.65 谷氨酸 2.19 9.67 4.25 4.60 3.22 甘氨酸 2.34 9.60 5.98 组氨酸 1.82 9.17 6.00 7.00 7.59 异亮氨酸 2.36 9.68 — 6.02 亮氨酸 2.30 9.60 — 5.98 蛋氨酸 2.28 9.21 — 5.74 赖氨酸 2.18 8.95 10.53 10.20 9.74 苯丙氨酸 1.83 9.13 — 5.48 脯氨酸 1.94 10.60 — 6.30
苄基 甘氨酰基 3 C H - + N H C H 2 C O O 第二部分与给定甘氨酸的转移自由能相似,因而从该氨基酸和甘氨酸的转移 自由能之差,可以表示出侧链的疏水性。 ∆ ∆ Gt 0 (侧链)= ∆ Gt 0 (氨基酸)—∆ Gt 0 (甘氨酸) 表 5-4 给出了某些氨基酸侧链的疏水性数值。用这些数据可以预测氨基酸在 疏水性载体上的吸附行为(它可作为疏水性的一个函数),像聚苯乙烯或连接脂 肪族C8或C18链的二氧化硅,吸附系数与疏水程度成正比。具有较大的正∆ Gt 0 的氨 基酸侧链是疏水性的,因此易溶于有机相而不是水相。蛋白质分子中的疏水氨 基酸残基倾向于处在蛋白质分子内部,氨基酸侧链的∆ Gt 0 为负值时则是亲水的, 这些氨基酸残基趋向于蛋白质分子表面。这里必须提出,赖氨酸尽管被认为是一 种亲水性氨基酸,但 △ Gt 0 为正值(这是由于它有 4 个易溶于有机相的-CH2- 基)。 事实上,蛋白质分子中的赖氨酸侧链被埋藏的同时,它的ε-氨基则突出在蛋白 质分子的表面。 表 5-3 氨基酸的 pKa 和 pI(25℃) 名称 pKa1 (α-COO- ) pKa2 (α-NH3 + ) pKaR (R=侧链) AA 侧链* pI 丙氨酸 2.34 9.69 — 6.00 精氨酸 2.17 9.04 12.48 >12.00 10.76 天冬酰胺 2.02 8.80 — 5.41 天冬氨酸 1.88 9.60 3.65 4.60 2.77 半胱氨酸 1.96 10.28 8.18 8.80 5.07 谷氨酰胺 2.17 9.13 - 5.65 谷氨酸 2.19 9.67 4.25 4.60 3.22 甘氨酸 2.34 9.60 5.98 组氨酸 1.82 9.17 6.00 7.00 7.59 异亮氨酸 2.36 9.68 — 6.02 亮氨酸 2.30 9.60 — 5.98 蛋氨酸 2.28 9.21 — 5.74 赖氨酸 2.18 8.95 10.53 10.20 9.74 苯丙氨酸 1.83 9.13 — 5.48 脯氨酸 1.94 10.60 — 6.30
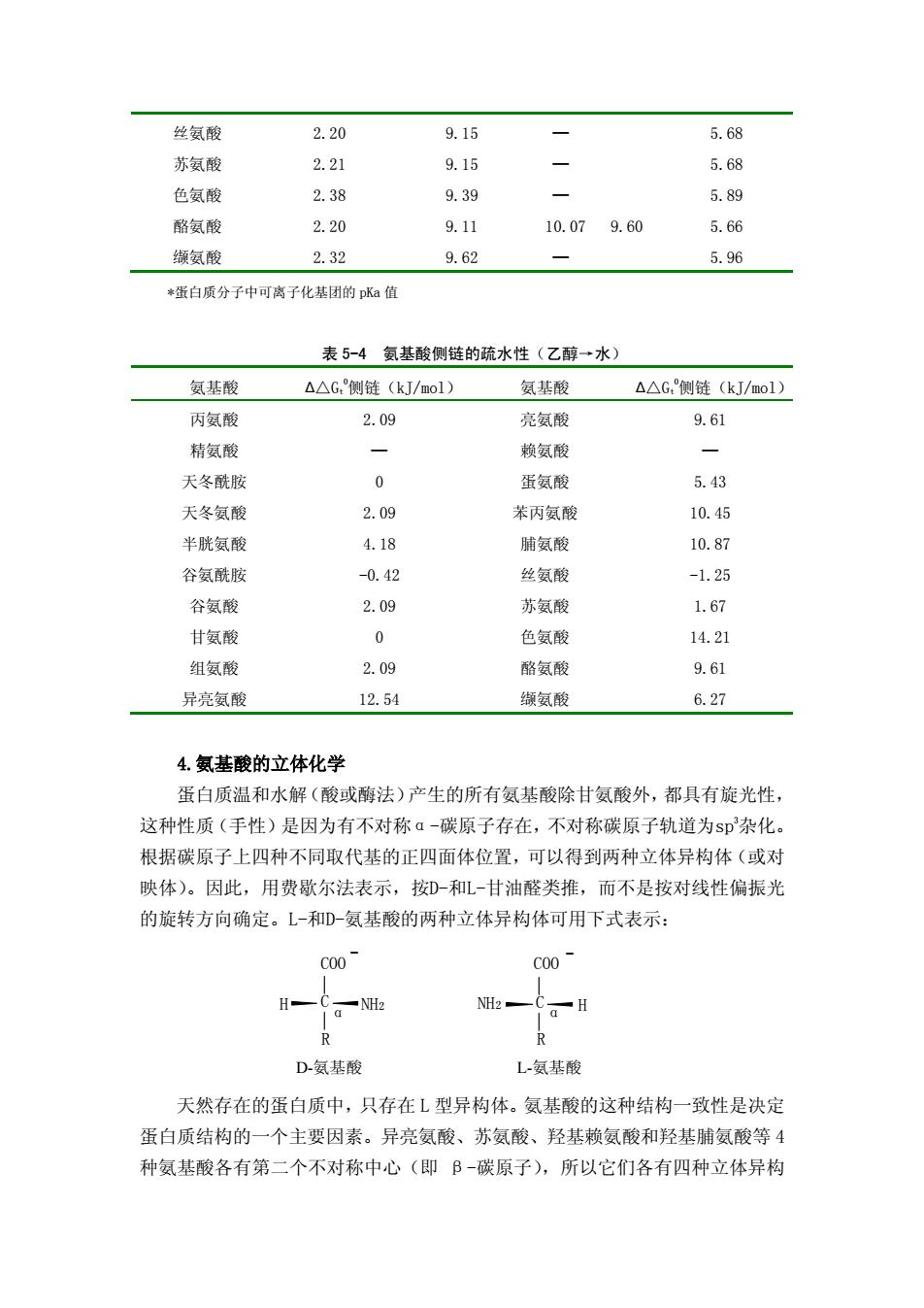
丝氨酸 2.20 9.15 — 5.68 苏氨酸 2.21 9.15 — 5.68 色氨酸 2.38 9.39 — 5.89 酪氨酸 缬氨酸 2.20 2.32 9.11 9.62 10.07 9.60 — 5.66 5.96 *蛋白质分子中可离子化基团的 pKa 值 表 5-4 氨基酸侧链的疏水性(乙醇→水) 氨基酸 ∆△Gt 0 侧链(kJ/mol) 氨基酸 ∆△Gt 0 侧链(kJ/mol) 丙氨酸 2.09 亮氨酸 9.61 精氨酸 — 赖氨酸 — 天冬酰胺 0 蛋氨酸 5.43 天冬氨酸 2.09 苯丙氨酸 10.45 半胱氨酸 4.18 脯氨酸 10.87 谷氨酰胺 -0.42 丝氨酸 -1.25 谷氨酸 2.09 苏氨酸 1.67 甘氨酸 0 色氨酸 14.21 组氨酸 异亮氨酸 2.09 12.54 酪氨酸 缬氨酸 9.61 6.27 4.氨基酸的立体化学 蛋白质温和水解(酸或酶法)产生的所有氨基酸除甘氨酸外,都具有旋光性, 这种性质(手性)是因为有不对称α-碳原子存在,不对称碳原子轨道为sp3 杂化。 根据碳原子上四种不同取代基的正四面体位置,可以得到两种立体异构体(或对 映体)。因此,用费歇尔法表示,按D-和L-甘油醛类推,而不是按对线性偏振光 的旋转方向确定。L-和D-氨基酸的两种立体异构体可用下式表示: N H 2 H R - C O O H N H C 2 R - C O O C α α D-氨基酸 L-氨基酸 天然存在的蛋白质中,只存在 L 型异构体。氨基酸的这种结构一致性是决定 蛋白质结构的一个主要因素。异亮氨酸、苏氨酸、羟基赖氨酸和羟基脯氨酸等 4 种氨基酸各有第二个不对称中心(即 β-碳原子),所以它们各有四种立体异构
丝氨酸 2.20 9.15 — 5.68 苏氨酸 2.21 9.15 — 5.68 色氨酸 2.38 9.39 — 5.89 酪氨酸 缬氨酸 2.20 2.32 9.11 9.62 10.07 9.60 — 5.66 5.96 *蛋白质分子中可离子化基团的 pKa 值 表 5-4 氨基酸侧链的疏水性(乙醇→水) 氨基酸 ∆△Gt 0 侧链(kJ/mol) 氨基酸 ∆△Gt 0 侧链(kJ/mol) 丙氨酸 2.09 亮氨酸 9.61 精氨酸 — 赖氨酸 — 天冬酰胺 0 蛋氨酸 5.43 天冬氨酸 2.09 苯丙氨酸 10.45 半胱氨酸 4.18 脯氨酸 10.87 谷氨酰胺 -0.42 丝氨酸 -1.25 谷氨酸 2.09 苏氨酸 1.67 甘氨酸 0 色氨酸 14.21 组氨酸 异亮氨酸 2.09 12.54 酪氨酸 缬氨酸 9.61 6.27 4.氨基酸的立体化学 蛋白质温和水解(酸或酶法)产生的所有氨基酸除甘氨酸外,都具有旋光性, 这种性质(手性)是因为有不对称α-碳原子存在,不对称碳原子轨道为sp3 杂化。 根据碳原子上四种不同取代基的正四面体位置,可以得到两种立体异构体(或对 映体)。因此,用费歇尔法表示,按D-和L-甘油醛类推,而不是按对线性偏振光 的旋转方向确定。L-和D-氨基酸的两种立体异构体可用下式表示: N H 2 H R - C O O H N H C 2 R - C O O C α α D-氨基酸 L-氨基酸 天然存在的蛋白质中,只存在 L 型异构体。氨基酸的这种结构一致性是决定 蛋白质结构的一个主要因素。异亮氨酸、苏氨酸、羟基赖氨酸和羟基脯氨酸等 4 种氨基酸各有第二个不对称中心(即 β-碳原子),所以它们各有四种立体异构