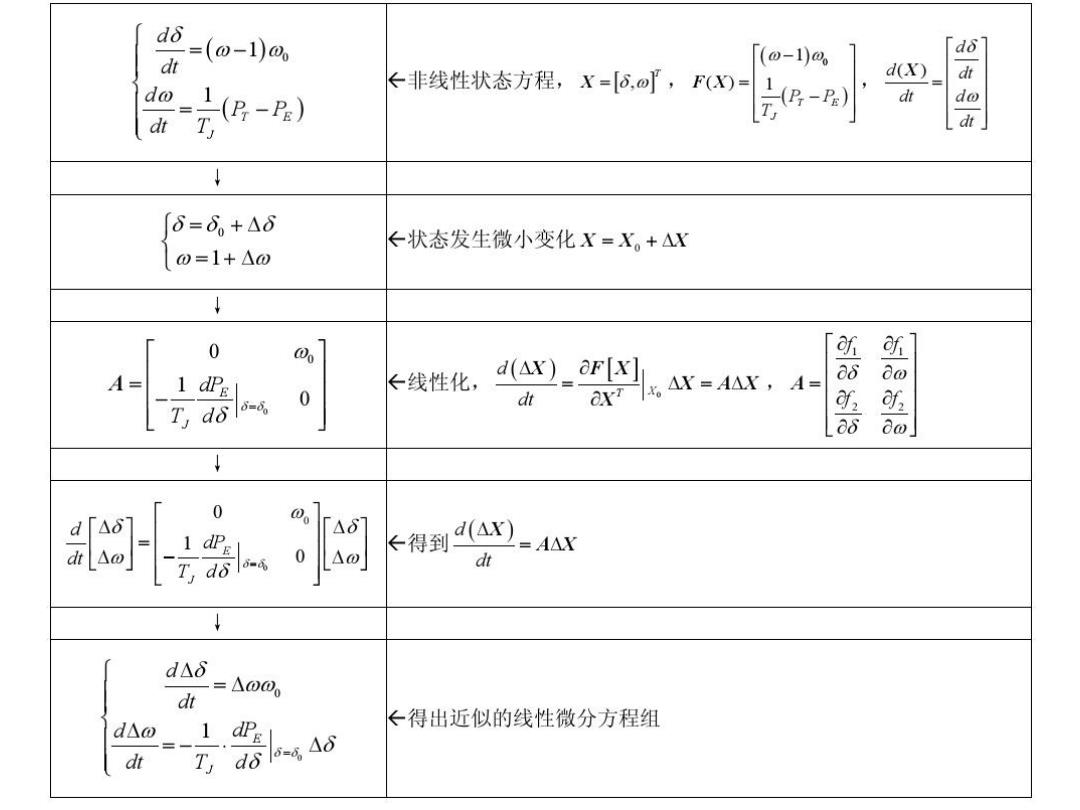
2-(w-1)o k非线性状态方程,X=[6,,FD- (o-1)4 d(x) 空-别 2-) [6=6,+△8 0=1+△o ←状态发生微小变化X=X。+△X ↓ 0 7 A= 长线性化, d(Ax)_oF[x] T,dols- 0 dt aN4A=a,A- 0 K得到4) A△X dt dAδ dt =△00 器 d△o1 ←得出近似的线性微分方程组 dt

d△ dt L-△000 d△o 1 dPE dt T,dδ9 6Aδ 就是系统状态变量偏移量的线性微分方程组
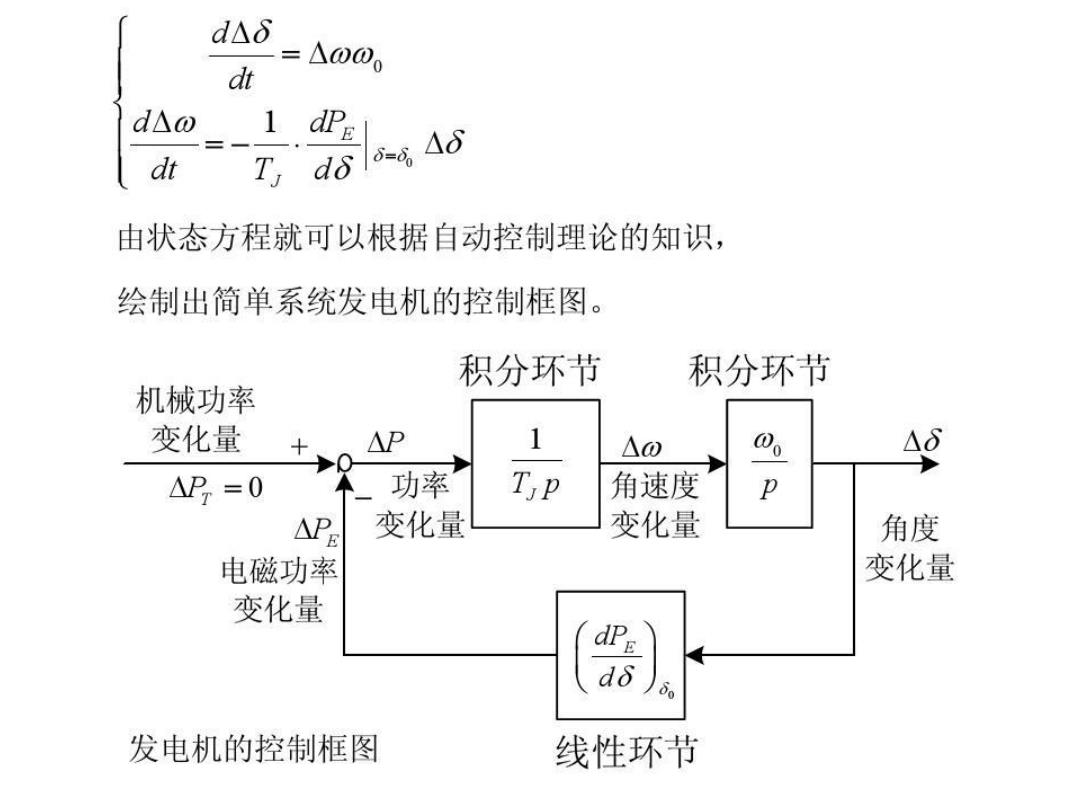
d△δ =△000 dt d△o -1 △8 dt 由状态方程就可以根据自动控制理论的知识, 绘制出简单系统发电机的控制框图。 积分环节 积分环节 机械功率 变化量 △P 1 △0 Aδ △P=0 「功率 T,P 角速度 P △PB 变化量 变化量 角度 电磁功率 变化量 变化量 do 发电机的控制框图 线性环节

(二)根据特征值判断系统的稳定性 对于线性系统,其微分方程的特征方程的根,也 就是其状态方程系数矩阵的特征值,可决定暂态 过程的变化规律。 。但是电力系统是非线性系统,经过线性化之后的 状态方程,用系数矩阵(雅克比矩阵)的特征值 来决定偏移量的变化规律是不可取的,但可以用 这种方法来判定系统是否稳定
(二)根据特征值判断系统的稳定性 对于线性系统,其微分方程的特征方程的根,也 就是其状态方程系数矩阵的特征值,可决定暂态 过程的变化规律。 但是电力系统是非线性系统,经过线性化之后的 状态方程,用系数矩阵(雅克比矩阵)的特征值 来决定偏移量的变化规律是不可取的,但可以用 这种方法来判定系统是否稳定

● 稳定: 所有特征值入∈(负实数U负实部的复数) ●】 边界: 所有特征值2c(负实数U负实部的复数)U(零U纯虚数) 不稳定: 只要出现一个正实数或一个具有正实部的复数的特征根