南京大学：《大学物理》课程教学资源（PPT讲座）Beam, beam, beam——无衍射光束的产生与调控

Nanjing University CEAS (Il)Bessel beam Helmhotz Equation u+ku =0 在柱坐标下变为 + 1 Ou ∂2u +k2u=0 令u(1,0,z)=v(r,0)Z(z),代入方程： 88+0+州 d'Z d22 继续作分离变量，分离r和0： Nat.Lab.Microstructures Dr.Tao LI,http://dsl.nju.edu.cn/litao

Nanjing University CEAS Nat. Lab. Microstructures Dr. Tao LI, http://dsl.nju.edu.cn/litao 2 2 Helmhotz Equation    u k u 0 在柱坐标下变为 2 2 2 2 2 2 1 1 1 ( ) 0 u u u u k u r r r r r z              2 2 2 2 2 2 1 1 1 [ ( ) ] v v d Z Z k v v r r r r r dz            令u r z v r Z z ( , , ) ( , ) ( ),    代入方程： 继续作分离变量，分离r和：

Nanjing University CEAS 作分离变量，引入常数几，得到： +片+(-加=0 1 Ov d'Z +2Z=0 dz2 接着令v(r,O)=R(r)Φ(O),代入得到： +6-网- 1d2Φ Φd02 Nat.Lab.Microstructures Dr.Tao LI,http://dsl.nju.edu.cn/litao

Nanjing University CEAS Nat. Lab. Microstructures Dr. Tao LI, http://dsl.nju.edu.cn/litao 作分离变量，引入常数，得到： 2 2 2 2 2 2 1 1 1 ( ) ( ) 0 0 v v k v r r r r r d Z Z dz                接着令v r R r ( , ) ( ) ( ),     代入得到： 2 2 2 2 1 1 [ ( ) ( ) ] r d dR d r k R R r dr dr d        

Nanjing University CEAS 最终得到三个分离变量微分方程： 1 d r dr 盟-2兰R=0 d2Φ cos(me) +=0 Φm(0)= 或 exp(ime) d02 sin(me) exp(-ime) d'Z cos(k.z) exp(ik.z) +λZ=0 Z(2)= 或 d=? sin(k) exp(-ik.z) 这里4=m2,元=k2。 令k2=k2-k2=k2-。此时方程(1)变为 1d Bessel方程 Nat.Lab.Microstructures Dr.Tao LI,http://dsl.nju.edu.cn/litao

Nanjing University CEAS Nat. Lab. Microstructures Dr. Tao LI, http://dsl.nju.edu.cn/litao 最终得到三个分离变量微分方程： 2 2 2 2 2 2 1 ( ) ( ) 0 0 0 d dR r k R r dr dr r d d d Z Z dz                cos( ) exp( ) ( ) sin( ) exp( ) m m im m im               或 cos( ) exp( ) ( ) sin( ) exp( ) z z z z k z ik z Z z k z ik z          或 2 2 2 2 2 2 , z r z m k k k k k       这里 。 令 。此时方程（1）变为 2 2 2 1 ( ) ( ) 0 r d dR m r k R r dr dr r    Bessel 方程

最 Nanjing University CEAS UNIVE 因此我们得到径向函数的通解 R(r)=CJ(kr)+DN(k.r) 由边界R(O)有限值，得到D=0。 所以最终的径向解就是Besseli函数Jm(kr)形式 而旋转切向则为振荡解，振荡波矢决定J的阶数！ Jo(x)- 0.5 1t) 08 J()-- 0.0 06 -0.5 0.4 -1.0 02 -1.5 0.d -2.0 0,3 -2.5 Y(x) Y,(x) 0.4 -3.0 Y2x)-- 10 15 20 10 15 20 X Nat.Lab.Microstructures Dr.Tao LI,http://dsl.niu.edu.cn/litao

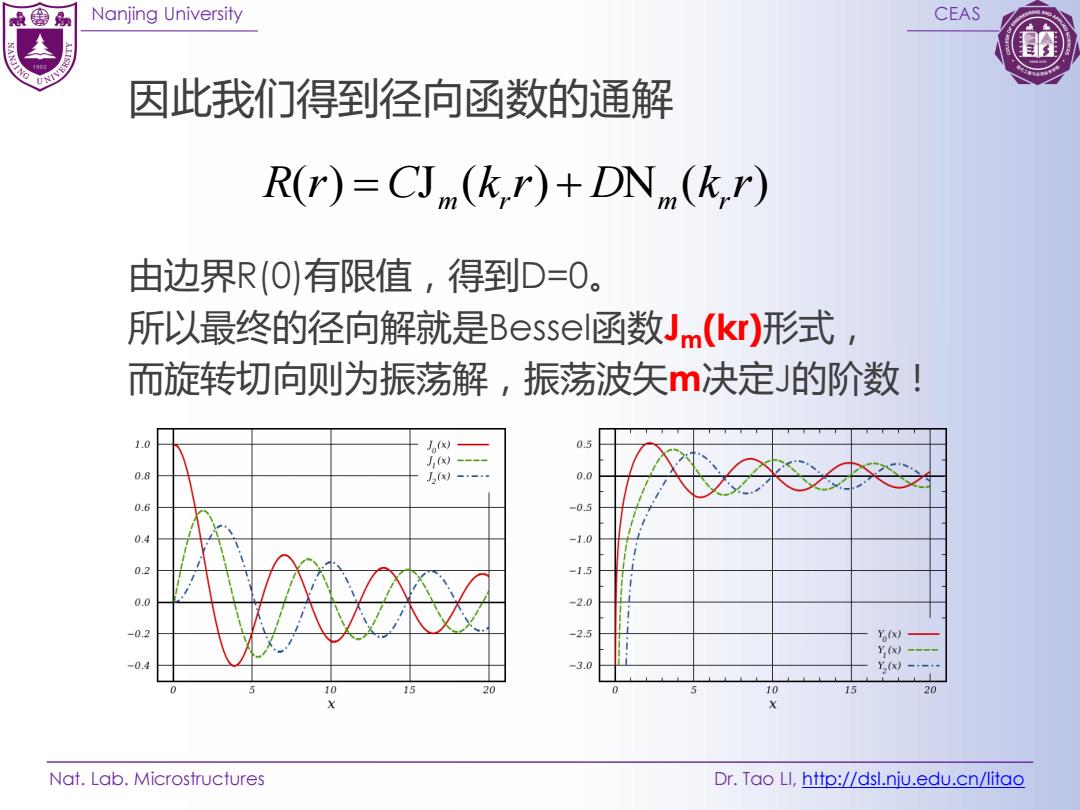
Nanjing University CEAS Nat. Lab. Microstructures Dr. Tao LI, http://dsl.nju.edu.cn/litao 因此我们得到径向函数的通解 由边界R(0)有限值，得到D=0。 所以最终的径向解就是Bessel函数Jm(kr)形式， 而旋转切向则为振荡解，振荡波矢m决定J的阶数！ ( ) J ( ) N ( ) R r C k r D k r   m r m r

最 Nanjing University CEAS UNIVE 零阶Bessel beam (m=0) Gaussian Beam Besser Beam Axicon 可 Nat.Lab.Microstructures Dr.Tao LI,http://dsl.niu.edu.cn/litao

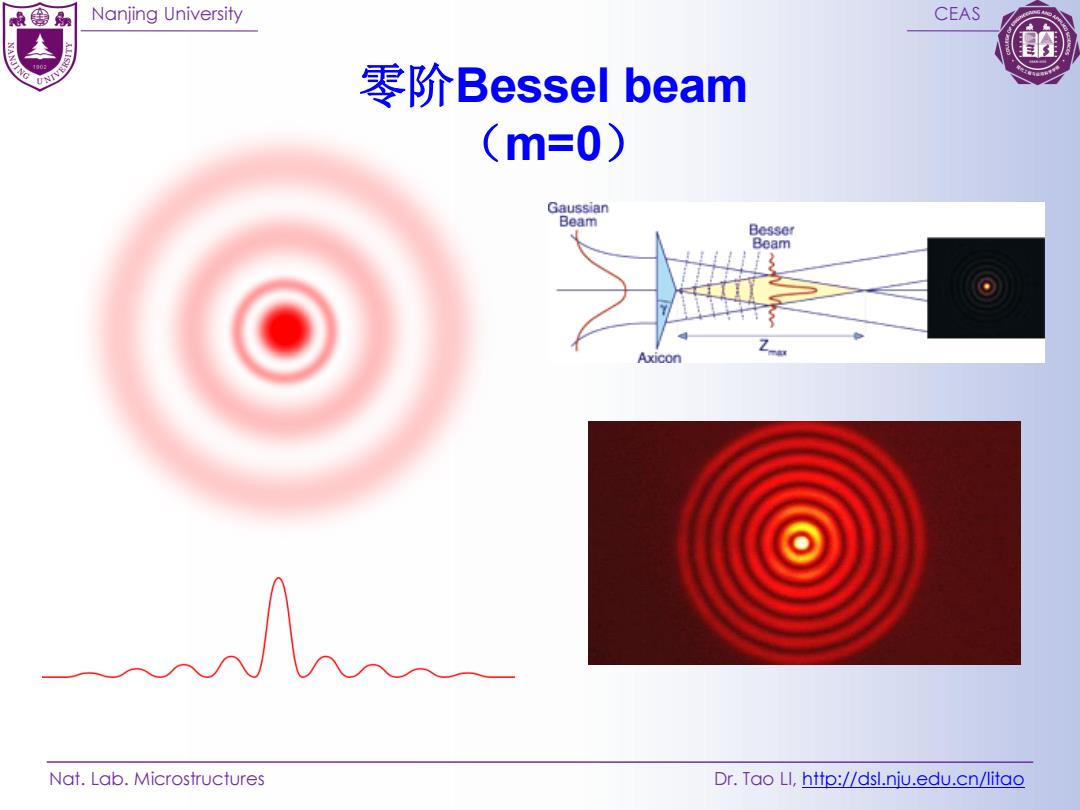
Nanjing University CEAS Nat. Lab. Microstructures Dr. Tao LI, http://dsl.nju.edu.cn/litao 零阶Bessel beam （m=0）