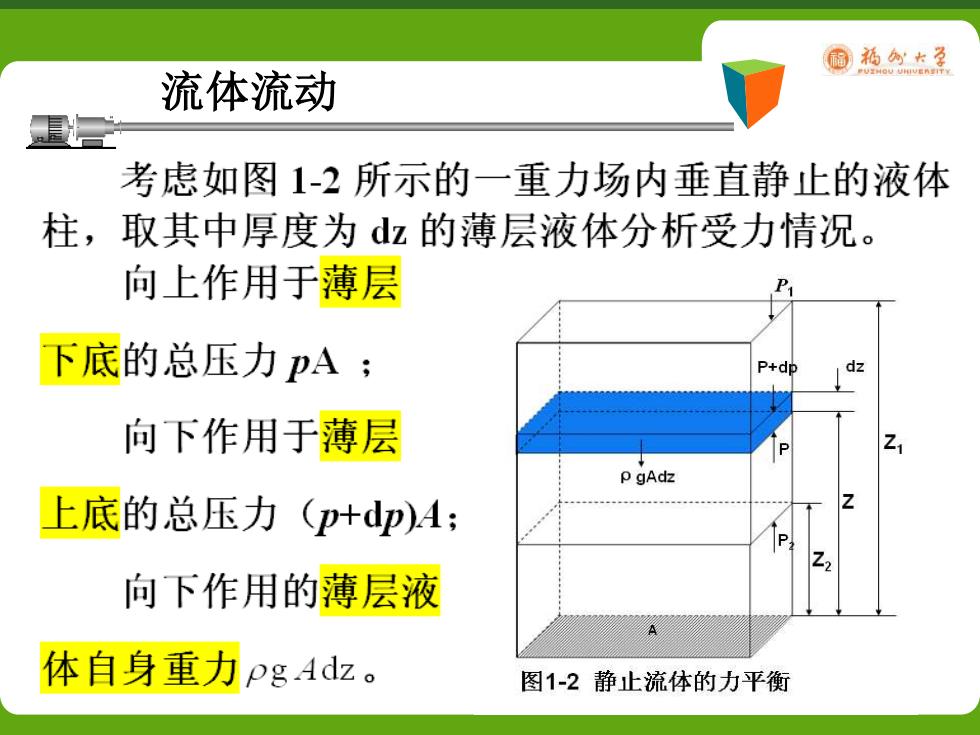
图福创大孕 流体流动 考虑如图1-2所示的一重力场内垂直静止的液体 柱,取其中厚度为dz的薄层液体分析受力情况。 向上作用于薄层 下底的总压力pA; P+dp 向下作用于薄层 p gAdz 上底的总压力(叶dp)A; 向下作用的薄层液 体自身重力pg Adz。 图1-2静止流体的力平衡
流体流动

福福卡学 流体流动 以向上作用的力为正,向下作用的力为负。流体静止时 三力之和为零,故 pA-(p+dp)4-pgAd=0 P+dp dz 简化得 Z p gAdz dp+pgdz 0 (1-3) Z P Z2 对于连续且不可压缩流体P 为常数,积分上式得 图1-2静止流体的力平衡
流体流动
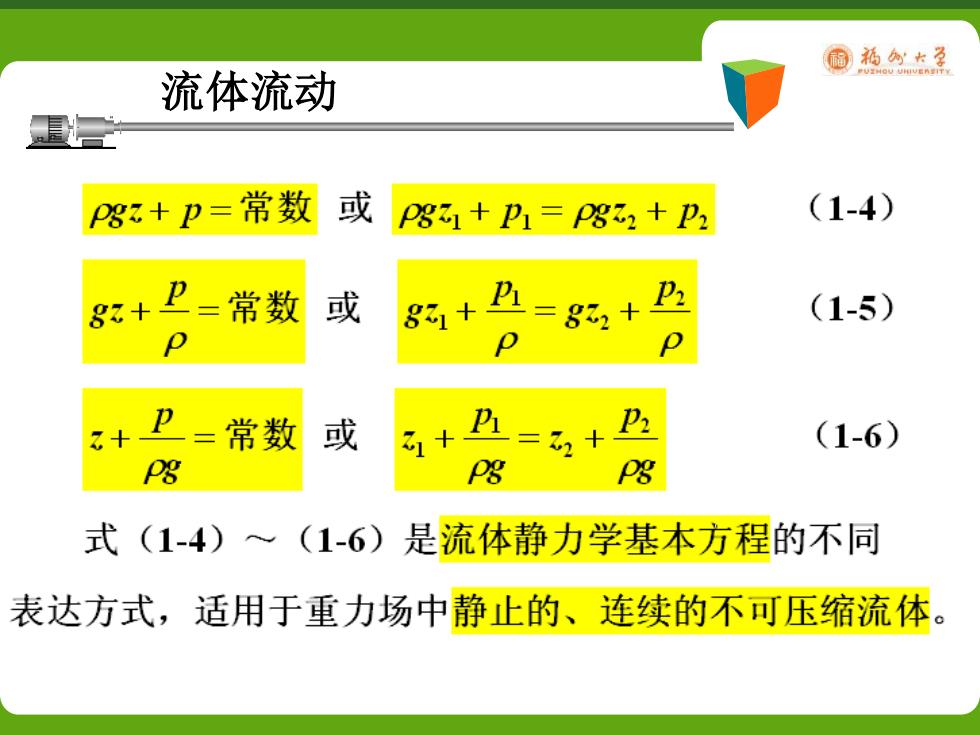
面瓶创卡孕 流体流动 P83+p=常数 或 P831+P1=P832+p2 (1-4) 82+ 卫=常数 或 &31+ =85,+B (1-5) +卫=常数 或 =2+乃 (1-6) 8 式(1-4)~(1-6)是流体静力学基本方程的不同 表达方式,适用于重力场中静止的、连续的不可压缩流体
流体流动
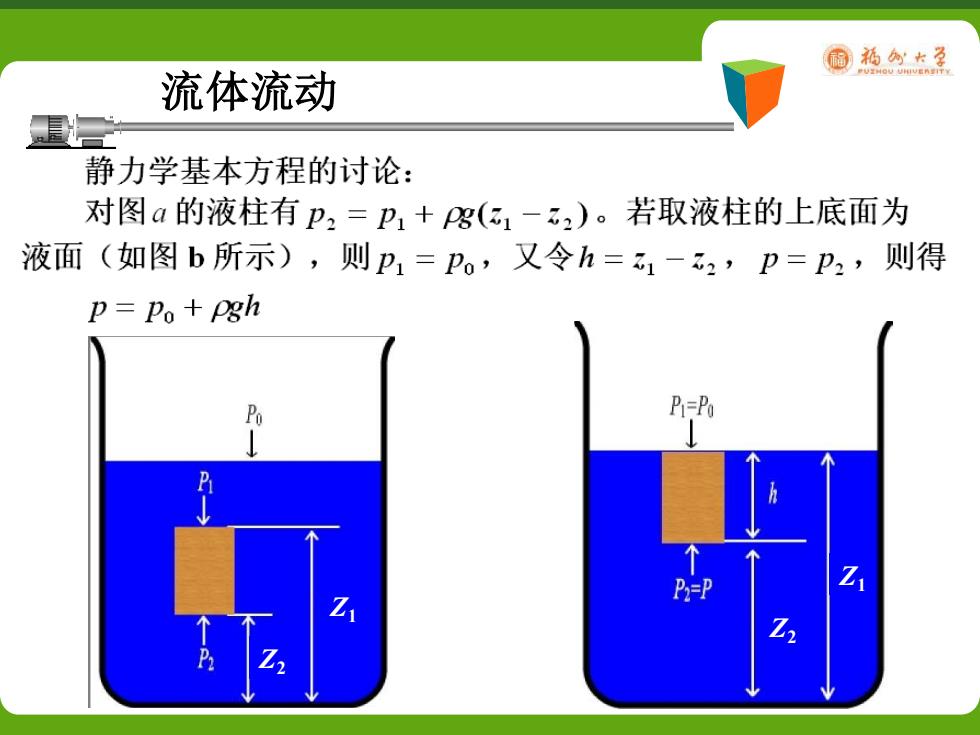
福福女学 流体流动 静力学基本方程的讨论: 对图a的液柱有P2=卫1+Pg(31-2)。若取液柱的上底面为 液面(如图b所示),则p1=P。,又令h=1-22,p=p2,则得 p=p。+Pgh P P1=Po Z Z
流体流动 Z1 Z2 Z1 Z2

图瓶创大学 流体流动 ①静止流体内部任一点的压力p与液体密度P及该点 距离液面的深度h有关。密度p越大或所处的位置h越深, 则该点的压力p就越大。 ② 巴斯噶原理 当液面上方的压力P,改变时,液体 内部各点的压力亦随之增减,即液面上所受的压力能以同样 大小传递到液体内部的任一点
流体流动