
eJ,ejot:基波分量(一次谐波分量) e2a,eJ2a:二次谐波分量 eNa,ewa:N次谐波分量 因此,一个由谐波关系的复指数线性组合成的信号: x(t)=∑ageo 该级数就是傅里叶级数, k=-∞ ak称为傅里叶级数的系数。 连续时间周期信号可以分解成无数多个复指数谐波分量 第3章周期信号的傅里叶级数表示 26
第3章 周期信号的傅里叶级数表示 26 因此,一个由谐波关系的复指数线性组合成的信号: tjtj ee 0 0 , − ωω : 基波分量(一次谐波分量) tjtj ee 0 0 22 , − ωω : 二次谐波分量 tjNtjN ee 0 0 , ω − ω : N次谐波分量 +∞ = −∞ = k tjk k eatx 0 )( ω 该级数就是傅里叶级数, a k 称为傅里叶级数的系数。 连续时间周期信号可以分解成无数多个复指数谐波分量

例1: 0)=cosa1-ee+e则 显然读信号中,有两个谐波分量,4=为相应分 量的加权因子,即傅里叶系数。 例2:x(t)=c0S0,t+2c0s30,t -lol+eJ+elia+ea 在该信号中,有四个谐波分量,即k=士1,士3, 时对应的谐波分量。 第3章周期信号的傅里叶级数表示 27
第3章 周期信号的傅里叶级数表示 27 例1: 0 xt t ( ) cos = ω 0 0 1 1 2 2 j t jt e e ω ω − = + 显然该信号中,有两个谐波分量, 为相应分 量的加权因子,即傅里叶系数 , 。 1 1 2 a± = 例2: 0 0 x( ) cos 2cos3 tt t = + ω ω 1 00 0 0 3 3 [ ] 2 j t jt j t j t ee e e ωω ω ω − − = + ++ 在该信号中,有四个谐波分量,即 k ±±= ,3,1 时对应的谐波分量

P131例题3.2 十3 己知:x()=xt+ID=∑ae2m k=-3 4=l,4=4=4,4=02=,4,=43=月 则,将具有相同谐波分量合在一起可重新写成: x(t)=? 第3章周期信号的傅里叶级数表示 28
第3章 周期信号的傅里叶级数表示 28 P131 例题3.2 + −= =+= 3 3 2 )()(: k tjk keaTtxtx 已知 π 则,将具有相同谐波分量合在一起,可重新写成: tx = ?)( 3 1 2 33 1 4 22 1 110 − − ,,,1 aaaaaaa − =======

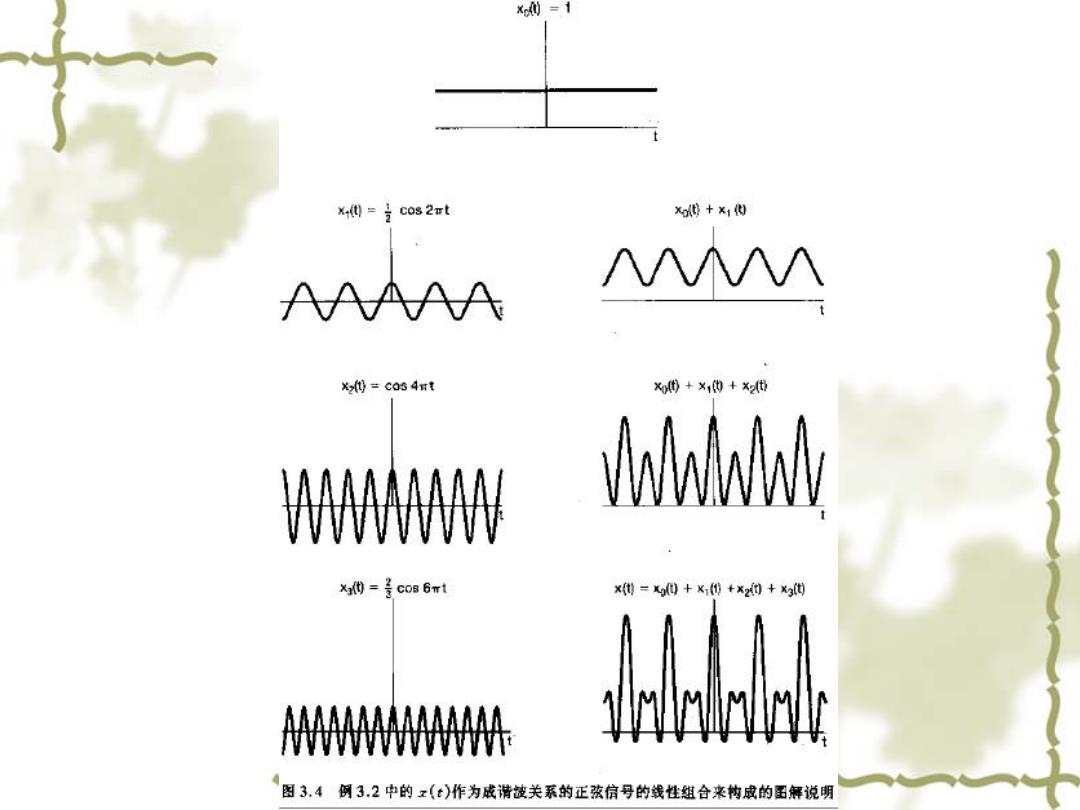
例3.2有一周期信号x()其基波频率为2π,写出3.25式 的形式为 +3 x)=∑a,e2m k=-3 其中a0=1,a1=1=1/4,2=a.2=1/2,3=0.3=1/3 将具有同一基波频率的谐波分量合在一起,得 e)=l+e2m+em)+e+e)+3e+e) 再用欧拉公式,x()可写成 2 x()=1+号cos2t+cos4πt+cos6mt 式3.28 2 式328是实周期信号傅里叶级数的另一种表现形式
例3.2 有一周期信号x(t)其基波频率为2π,写出3.25式 的形式为 其中a0 =1,a1 =a-1 =1/4,a2 =a-2 =1/2,a3 =a-3 =1/3 将具有同一基波频率的谐波分量合在一起,得 再用欧拉公式,x(t)可写成 式3.28是实周期信号傅里叶级数的另一种表现形式。 3 2 3 ( ) jk t k k xt ae π + =− = 111 22 44 66 () 1 ( ) ( ) ( ) 423 j t jt jt jt jt jt xt e e e e e e ππ ππ ππ − −− =+ + + + + + 1 2 ( ) 1 cos 2 cos 4 cos 6 2 3 xt t t t =+ + + ππ π 式3.28
x0)=1 x0=支c082rt +×1因 AAAA M x>(t)=cos 4ut X0+0+用 wwiwtw x0=号co86mt x=0+K+×2甜+30 AAMAAAAAAAAAAAN WWΨ VVVVVVVVVVVVVVT 图3.4例3.2中的z(:)作为成请凌关系的正弦信号的线性组合来构成的图解说明