
2、直线的标高投影、直线的坡度和平距 。 直线的标高投影:可由直线上任意两点的标高投影或直线上一点 的标高投影及该直线的方向确定。 直线的坡度:直线上任意两点的高程差与对应的水平距离之比称 为,用字母表示,i=H/儿,与数学上的斜率概念类似。 上式表示两点间的水平距离为1个单位()时两点的高度差即等于坡度。 ·直线的平距:当直线上两点之间的高差为1时,对应的水平距离 数值。可见l=L/H=1/i。 坡度和平距都能反映直线的倾斜程度。 由此可见,平距是坡度的倒数,坡度大则平距小,坡度小则平距 大。 0是46日 123
2、直线的标高投影、直线的坡度和平距 • 直线的标高投影:可由直线上任意两点的标高投影或直线上一点 的标高投影及该直线的方向确定。 • 直线的坡度:直线上任意两点的高程差与对应的水平距离之比称 为,用字母i表示,i=H/L,与数学上的斜率概念类似。 上式表示两点间的水平距离为1个单位(m)时两点的高度差即等于坡度。 • 直线的平距l:当直线上两点之间的高差为1时,对应的水平距离 数值。可见l=L/H=1/i。 坡度和平距都能反映直线的倾斜程度。 • 由此可见,平距是坡度的倒数,坡度大则平距小,坡度小则平距 大
直线的表示法 ①两点表示直线,即通过直线上两点的标高投影确定直线, ②直线上一点的标高投影及直线的坡度和方向,用坡度和H面 投影上箭头所指出的下降方向表示,一般箭头指向下坡,根 据坡度=1就可以唯一地确定这条直线的空间位置。 等高线:水平线因平行于面,水平线上所有点的高程都相同, 所以水平线称为等高线。等高线只要画出它的面投影并注 明其高程数,也就可以唯一地确定该等高线的空间位置。 04 92 206 .C2C6 12 02 fe 0 1234 01234 e2i=1
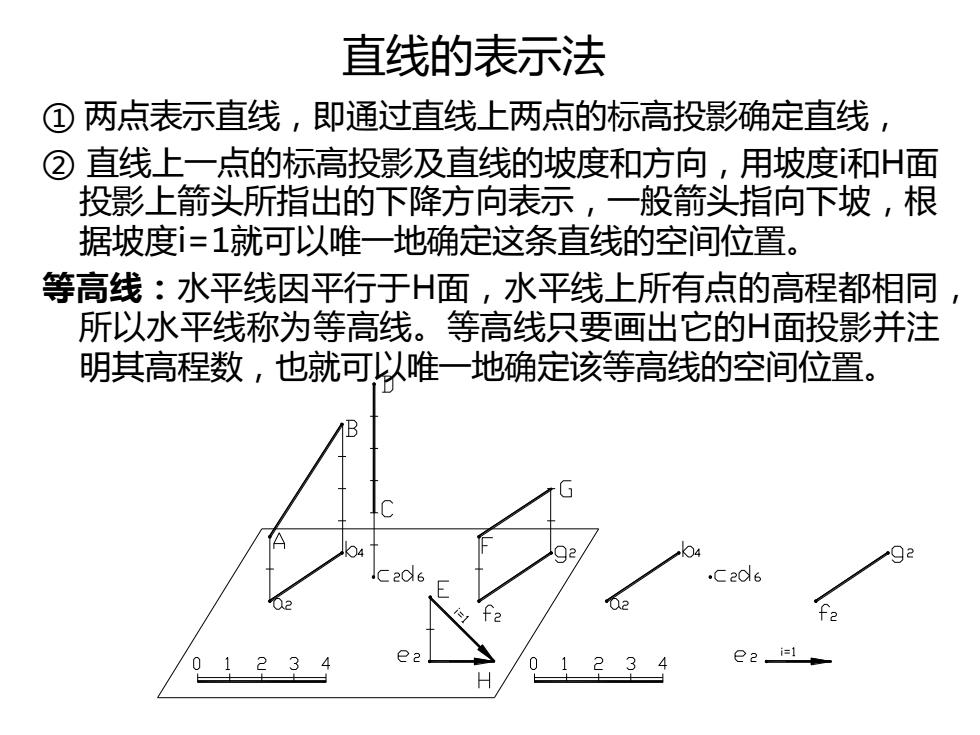
直线的表示法 ① 两点表示直线,即通过直线上两点的标高投影确定直线, ② 直线上一点的标高投影及直线的坡度和方向,用坡度i和H面 投影上箭头所指出的下降方向表示,一般箭头指向下坡,根 据坡度i=1就可以唯一地确定这条直线的空间位置。 等高线:水平线因平行于H面,水平线上所有点的高程都相同, 所以水平线称为等高线。等高线只要画出它的H面投影并注 明其高程数,也就可以唯一地确定该等高线的空间位置

直线的实长及确定整数高程点 在标高投影中求直线的实长,仍然采用正投影中的直角 三角形法。以直线的标高投影为一直角边;直线两端点的高 程差为另一直角边,作直角三角形,该直角三角形的斜边为 直线的实长,角为直线对基准面的倾角。 在实际工作中常遇到直线的两端点的标高数字并非整数 需要在直线的投影上定出各整数标高点,这些整数标高点称 为刻度。 。求整数标高点有两种方法: 计算法(先求出直线的坡度再利用坡度求其他点的投(如前 例) 图解法
直线的实长及确定整数高程点 • 在标高投影中求直线的实长,仍然采用正投影中的直角 三角形法。以直线的标高投影为一直角边;直线两端点的高 程差为另一直角边,作直角三角形,该直角三角形的斜边为 直线的实长,角为直线对基准面H的倾角。 在实际工作中常遇到直线的两端点的标高数字并非整数, 需要在直线的投影上定出各整数标高点,这些整数标高点称 为刻度。 • 求整数标高点有两种方法: 计算法(先求出直线的坡度再利用坡度求其他点的投(如前 例) 图解法
二、平面的标高投影 : ()平面上的等高线 平面上的水平线称为等高线 直线上的任意点的高程都相 等高找 一最大拔度线 等,等高线彼此平行,当高程 差相等时,对应的水平距离也 01 相等。 常取平面上整数标高的水平 度比例尺 线为等高线。,并把平面与基准 面(H面)的交线作为高程为 01234 01234 零的等高线。 等高线具有以下特性: ①等高线是直线; ②等高线互相平行; ③等高线平距相等。 (2)坡度比例尺 将平面上的最大坡度线的投 影附以整数高程,并画成一粗 一细的双线。坡度比例尺与等 高线垂直。坡度比例尺上的刻 度间距就是等高线的平距
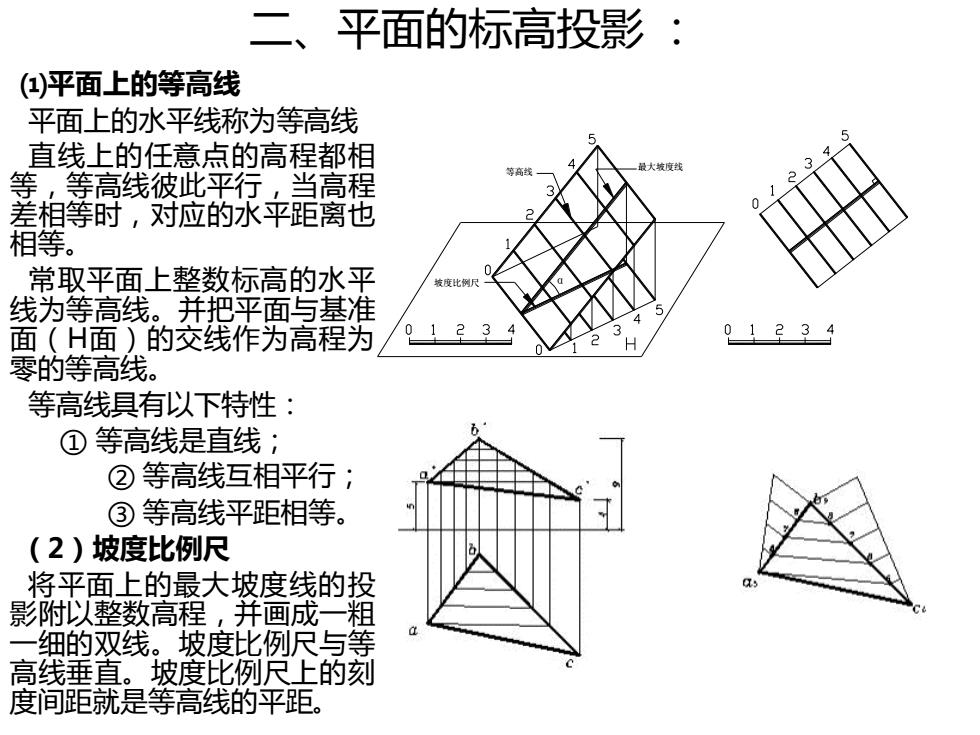
二、平面的标高投影 : ⑴平面上的等高线 平面上的水平线称为等高线 直线上的任意点的高程都相 等,等高线彼此平行,当高程 差相等时,对应的水平距离也 相等。 常取平面上整数标高的水平 线为等高线。并把平面与基准 面(H面)的交线作为高程为 零的等高线。 等高线具有以下特性: ① 等高线是直线; ② 等高线互相平行; ③ 等高线平距相等。 (2)坡度比例尺 将平面上的最大坡度线的投 影附以整数高程,并画成一粗 一细的双线。坡度比例尺与等 高线垂直。坡度比例尺上的刻 度间距就是等高线的平距。 坡度比例尺 最大坡度线 等高线 α

平面内的坡度线: 平面内对水平面的最大斜度线就是平面内的 坡度线。 特性: (1)、平面内的坡度线与等高线互相垂直,它们 的水平投影也互相垂直; (2)、平面内坡度线的坡度就代表平面的坡度 坡度线的平距就是平面内等高线间的平距
平面内的坡度线: 平面内对水平面的最大斜度线就是平面内的 坡度线。 特性: (1)、平面内的坡度线与等高线互相垂直,它们 的水平投影也互相垂直; (2)、平面内坡度线的坡度就代表平面的坡度, 坡度线的平距就是平面内等高线间的平距