3-1 负指数分布 车头时距服从负指数分布的车流特性见图,曲 线是单调下降的,说明车头时距愈短,出现的 概率愈大。这种情形在不能超车 的单列车流中是不可 能出现的,因为车辆 1.2 的车头与车头之间至 少存在一个车长,所 0. 以车头时距必有一个 2.0 大于零的最小值ī。 t(时间)
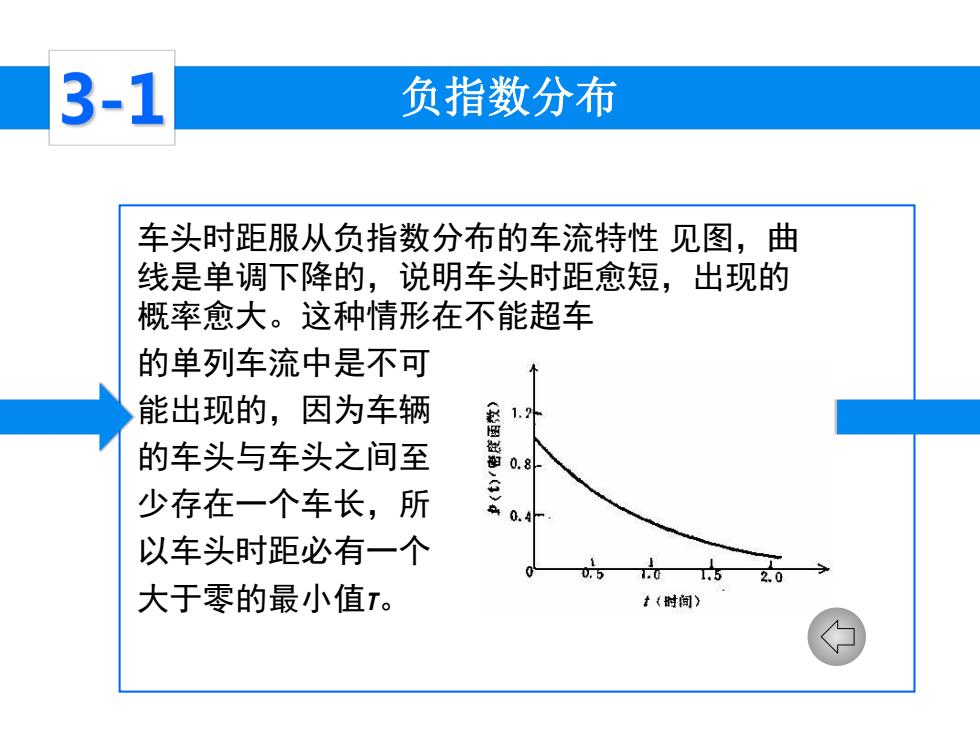
负指数分布 车头时距服从负指数分布的车流特性 见图,曲 线是单调下降的,说明车头时距愈短,出现的 概率愈大。这种情形在不能超车 的单列车流中是不可 能出现的,因为车辆 的车头与车头之间至 少存在一个车长,所 以车头时距必有一个 大于零的最小值τ

3-2 移位负指数分布 适用条件:用于描述不能超车的单列车流 的车头时距分布和车流量低的车流的车头 时距分布。 移位负指数分布公式: P(h>t)=e-A(-) (t≥T) P(h≤t)=1-e-) (t≥t) ·分布的均值和方差D分别为: M=1+t
移位负指数分布 :用于描述不能超车的单列车流 的车头时距分布和车流量低的车流的车头 时距分布。 : : ( ) 1 ( ) ( ) ( ) ( ) ( ) P h t e t P h t e t t t 2 1 1 M D

3-2 移位负指数分布 移位负指数分布的局限性: 服从移位负指数分布的车头时距愈接近τ 出现的可能性愈大。这在一般情况下是不 符合驾驶员的心理习惯和行车特点的。 ● 车头时距分布的概率密度曲线一般总是先 升后降
移位负指数分布 服从移位负指数分布的车头时距愈接近τ 出现的可能性愈大。这在一般情况下是不 符合驾驶员的心理习惯和行车特点的。 车头时距分布的概率密度曲线一般总是先 升后降
【例题】在一条有隔离带的双向四车道道路 上,单向流量为360辆h,该方向路宽7.5m ,设行人步行速度为1mls,求h中提供给行 人安全横过单向车道的次数,如果单向流量 增加到900辆h,1h中提供给行人安全横过 单向车道的次数是增加还是减少 Q=360辆/h=■
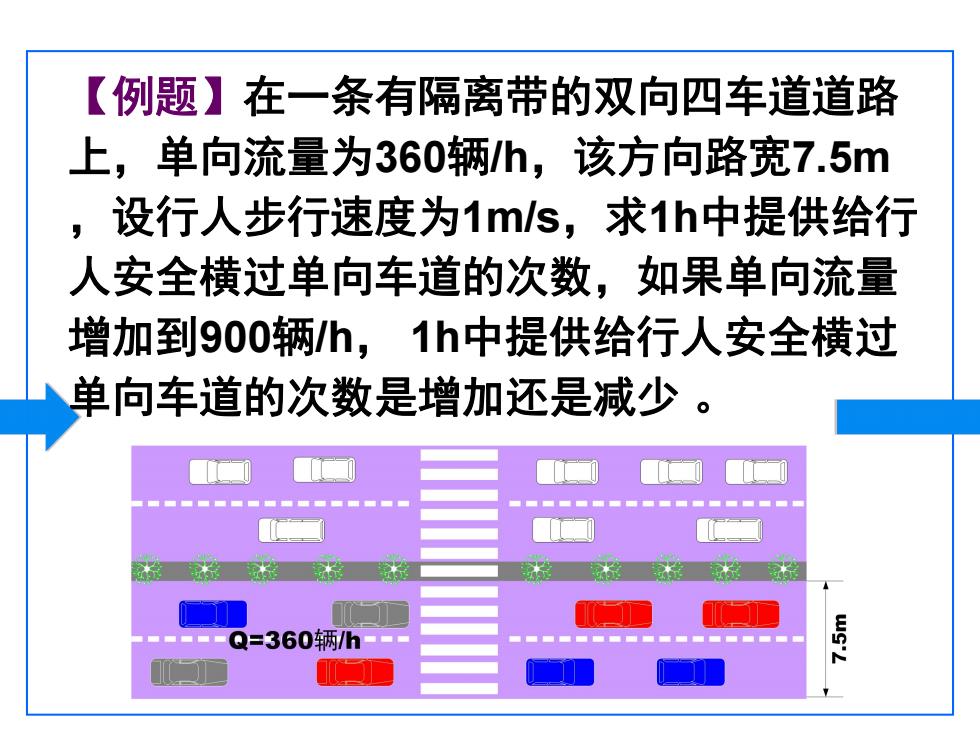
【例题】在一条有隔离带的双向四车道道路 上,单向流量为360辆/h,该方向路宽7.5m ,设行人步行速度为1m/s,求1h中提供给行 人安全横过单向车道的次数,如果单向流量 增加到900辆/h, 1h中提供给行人安全横过 单向车道的次数是增加还是减少

解:行人横过单向行车道所需要的时间: t=7.5/1=7.5s 因此,只有当275s时,行人才能安全穿 越,由宇双军道道路可以充分超车,全头时 距符合负指数分布,对于任意前后两辆车而 言,车头时距大于75s的概率为: -24_360x7.5 Ph≥75)=e3600=e3600=0.4724 对于Q360辆h的车流,1h车头时距次数 为360,.其中27.5s的车头时距为可以安全 横穿的次数: 360×0.4724=170 (次)
解:行人横过单向行车道所需要的时间: t =7.5/1=7.5s 因此,只有当h≥7.5s时,行人才能安全穿 越,由于双车道道路可以充分超车,车头时 距符合负指数分布,对于任意前后两辆车而 言,车头时距大于7.5s的概率为: 对于 Q=360辆/h的车流,1h车头时距次数 为360,其中h≥7.5s的车头时距为可以安全 横穿的次数: 0 4724 3600 360 7 5 3600 7 5 . . ( . ) P e e Qt h 360 0.4724 170 (次)