川北医学院：《模拟电子技术基础》课程电子教案（课件讲稿）09 信号处理与信号产生电路

4.n阶巴特沃斯传递函数 传递函数为 A(j)= 1+(o1o.)24 式中n为阶滤波电路阶数，o为3dB截止角频率，A,为通带电 压增益。 |A(jw)川 Ao 1.0 0.9 理想 0.8 n=1 0.7 0.6 0.5F n=1 0.4 n=2 0.3 0.2 n=4 n=3 0.1 0 0 0.20.40.60.81.01.21.41.61.82.0w/wc

4. n阶巴特沃斯传递函数 传递函数为 2n c 0 1 ( / ) (j )      A A 式中n为阶滤波电路阶数，c为3dB截止角频率，A0为通带电 压增益

9.3.2 有源高通滤波电路 1.二阶高通滤波电路 将低通电路中的电 容和电阻对换，便成为 71 高通电路。 (AVF-1)RI 传递函数 A(S)= A02 R 同相比例 52+ S+0 放大电路 归一化的幅频响应 201g A(j@) o =20lg g-+ c 川北医学院生物医学工程

9.3.2 有源高通滤波电路 1. 二阶高通滤波电路 将低通电路中的电 容和电阻对换，便成为 高通电路。 传递函数 2 c 2 c 2 0 ( )      s Q s A s A s c 2 2 c 2 0 ( ) 1 ( ) 1 20lg (j ) 20lg Q A A              归一化的幅频响应 

2.巴特沃斯传递函数及其归一化幅频响应 Ao j)-. 归一化幅频响应 |A(jω)川 Ao 1.0 0.9 0.8 n=3 n=2 n=1 S554S2 n=4 0 0.20.40.60.81.01.21.41.61.82.0w/0c 川心堡子屍三物堡子L程

2. 巴特沃斯传递函数及其归一化幅频响应 2n 0 1 ( / ) ( )    c A A j   归一化幅频响应

9.3.3有源带通滤波电路 1.电路组成原理 V1 00 低通 高通 可由低通和高通串联得到 4 0H= RCi 低通截止角频率 1 低通 01= 高通截止角频率 R,C2 OH |A4 必须满足0L<oH 高通 0 「 o L4 带通 比医学院生 L WH @

9.3.3 有源带通滤波电路 1. 电路组成原理 可由低通和高通串联得到 必须满足 1 1 H 1 R C   低通截止角频率 2 2 L 1 R C   高通截止角频率 L  H

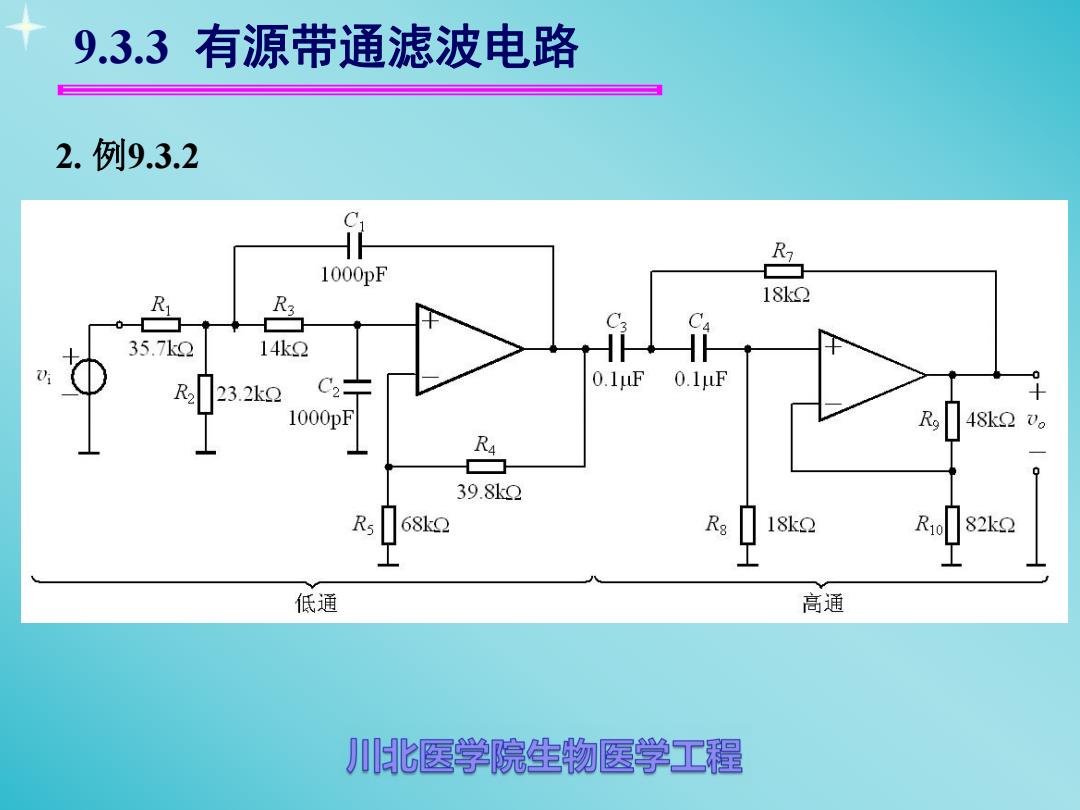
9.3.3 有源带通滤波电路 2.例9.3.2 1000pF R R3 18k2 0 白 35.7k2 14k2 23.2k2 C2卡 01F 0.1F 1000pF 482'o 凸 39.8k2 R 68k2 18k2 R10 82k2 工 低通 高通 1北医学院生物医学工程

2. 例9.3.2 9.3.3 有源带通滤波电路