
弯曲应力和强度计算剪力:左上右下为正弯矩:左顺右逆为正
16 剪力:左上右下为正 弯矩:左顺右逆为正

弯曲应力和强皮计算二、例题[例1]:求图(a)所示梁1--1、2--2截面处的内力。q解:截面法求内力。qL1--1截面处截取的分离体2h如图(b)示。7ZY = qL+Q, =0图(a).. Q - -qLqLMiZm (F)= qLx + M =0Q.: M, = -qLx图(b)17
17 [例1]:求图(a)所示梁1-1、2-2截面处的内力。 x y Q qL Y qL Q = − = + = 1 1 0 解:截面法求内力。 1-1截面处截取的分离体 如图(b)示。 图(a) 1 1 1 1 ( ) 0 M qLx mA Fi qLx M = − = + = 二、例题 q qL 1 a b 1 2 2 qL Q1 A M1 图(b) x1
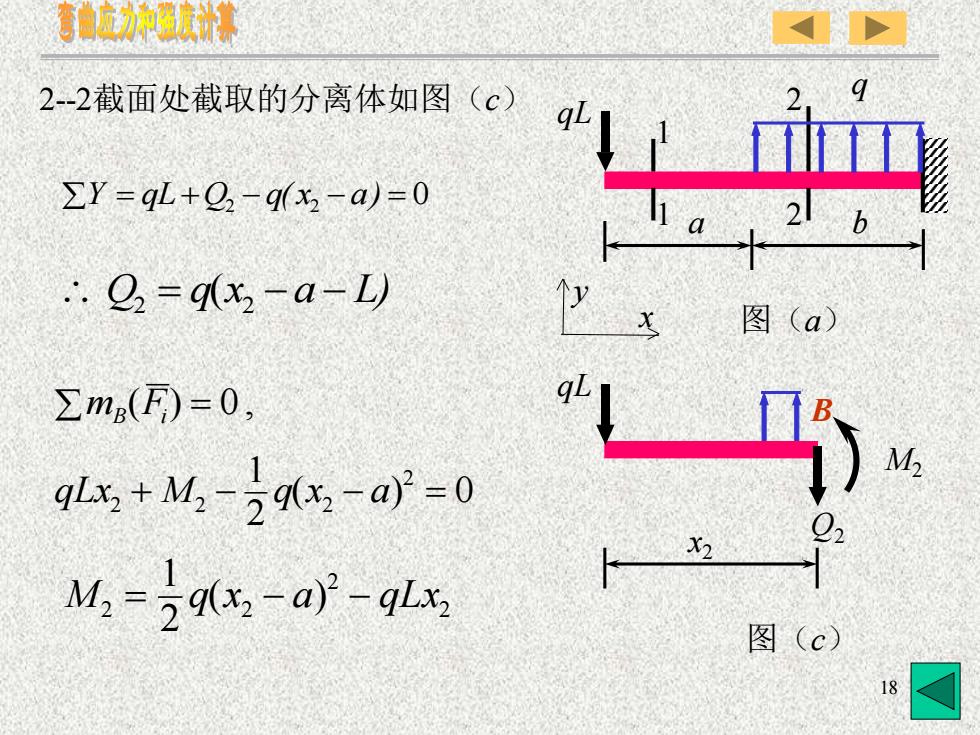
弯曲应力和强度计算2--2截面处截取的分离体如图(C)qLZY= qL+Q, - q(x -a) =0.: Q, = q(x, - α- L)图(a)qLZm(F)= 0,福M2qlx, + M,-g(, -a) =0Q2X2M, -g(, -a) - qLx图(c)18
18 Q = q x −a − L) 2 2 ( qLx M q x a mB Fi ( ) 0 2 1 ( ) 0 , 2 2 + 2 − 2 − = = 2-2截面处截取的分离体如图(c) Y = qL +Q2 − q( x2 − a) = 0 2 2 2 2 ( ) 2 1 M = q x − a − qLx x y 图(a) q qL 1 a b 1 2 2 qL Q2 B M2 x2 图(c)

弯曲应力和强度计算例2 求图示外伸梁在截面1--1、22、3-3和44横截面上的剪力和弯矩tyM.-3FaFB1A231.41.8.234工人aOFBIF2a解:支反力为ZM,=0F,×2a+3Fa+ F×a=0F: = -2F(1)ZF,-0F:+F =F F =3F(T)19
19 例2 求图示外伸梁在截面1—1、2—2、3—3和4— 4横截面上的剪力和弯矩。 解:支反力为 Fy = 0 M A = 0 FB 2a +3Fa + F a = 0 F = −2F() B FB + FA = F F = 3F() A x y A F B a a 2a 1 1 2 2 4 4 3 3 Me =3Fa FA FB

弯曲应力和强度计算yM。=3FaFB1A2341.8.2x34aaTFB2aTF截面1—1ZF,=0Fsi = --FFcTM +Fxa=0ZAMci =0M8M,=-Fa(顺)1 Fs1截面2——2ZF,=0 F,-F+F-0F2Fs2 -F-F=2FC2-M2IMc=0 M,+Fxa=0FA 2Fs2M,=-Fa(顺)
20 截面 1 — 1 Fy = 0 M C 1 = 0 M 1 + F a = 0 ( ) M 1 = −Fa 顺 FS 1 = − F 截面 2 — 2 Fy = 0 M C 2 = 0 M 2 + F a = 0 ( ) M 2 = −Fa 顺 FS 2 − FA + F = 0 FS 2 = FA − F = 2 F M1 FS1 F C 1 11 FA M2 FS2 F C2 22 x y A F B a a 2 a 11 22 44 33Me =3Fa FA FB