temp-temp+d(S(i).S(i+1)) end empSum-temp. end c130L-20,a09,T- %退火过程 for k=1:L %产生新解 c-2+floor(100*rand(1.2) c1=c1)c2=c(2) %计算代价函数值 1).SO(c2))+d(SO(c1).SO(c2+1)}-d(SO(c1-1).SO(c1))-d(SO(c2).SO(c2+1)): ifdf<0 S0S0(1:c1-1),S0c2:-1:cl),S0(c2+1:102 elseif e Sum+ and(1 s0=s01c1-l.s0(c2-1:cl),s0c2+1:102 Sum=Sum+df; if T<e break end 计算结果为44小时左右。其中的一个巡航路径如图1所示。 图1模拟退火算法求得的遮航路径示意图
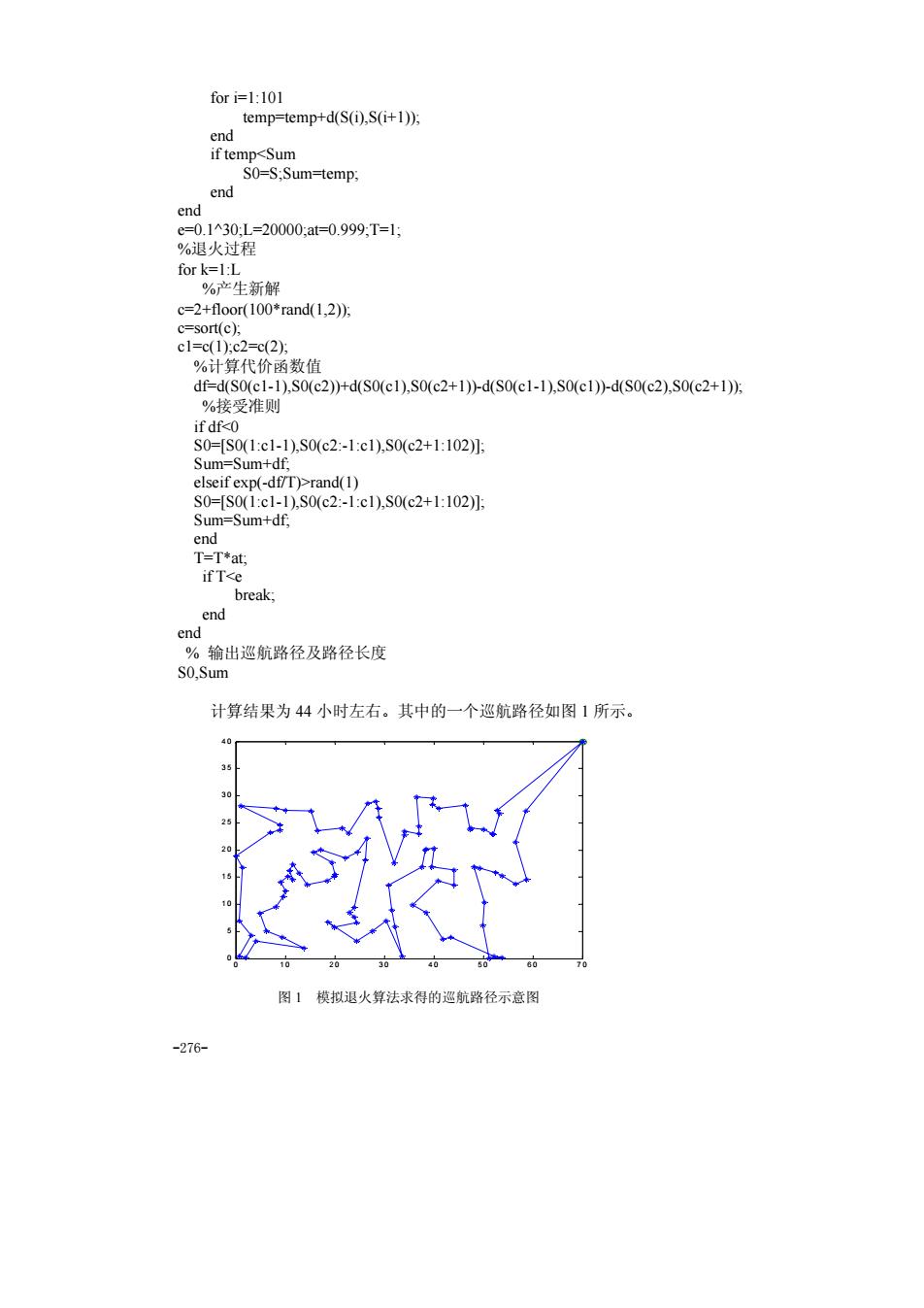
-276- for i=1:101 temp=temp+d(S(i),S(i+1)); end if temp<Sum S0=S;Sum=temp; end end e=0.1^30;L=20000;at=0.999;T=1; %退火过程 for k=1:L %产生新解 c=2+floor(100*rand(1,2)); c=sort(c); c1=c(1);c2=c(2); %计算代价函数值 df=d(S0(c1-1),S0(c2))+d(S0(c1),S0(c2+1))-d(S0(c1-1),S0(c1))-d(S0(c2),S0(c2+1)); %接受准则 if df<0 S0=[S0(1:c1-1),S0(c2:-1:c1),S0(c2+1:102)]; Sum=Sum+df; elseif exp(-df/T)>rand(1) S0=[S0(1:c1-1),S0(c2:-1:c1),S0(c2+1:102)]; Sum=Sum+df; end T=T*at; if T<e break; end end % 输出巡航路径及路径长度 S0,Sum 计算结果为 44 小时左右。其中的一个巡航路径如图 1 所示。 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 0 5 1 0 1 5 2 0 2 5 3 0 3 5 4 0 图 1 模拟退火算法求得的巡航路径示意图

§2遗传算法 2.1 传算法简介 算 话Genetic Algorithms 简称GA)是 实质是通过群体搜案技术,根 初始 生存的原则 根据适者生存的原则选择优良个体、被选出的优良个体两两配对,通过随机交叉其染色 体的基因并随机变异某些染色体的基因后生成下一代群体,按此方法使群体逐代进化, 直到满足进化终止条件。其实现方法如下: (1)根据具体问题确定可行解域,确定一种编码方法,能用数值串或字符串表示 可行解域的每一 (2)对每 一解应有一个度量好坏的依据,它用一函数表示,叫做适应度函数,适 应度函数应为非负函数。 (3)确定进化参数群体规模M、交叉概率P。、变异概率Pm、进化终止条件。 为便于计算,一般米说,每一代群体的个体数目都取相等。群体规模越大、越容 易找到最优解,但由于受到计算机的运算能力的限制,群体规模越大,计算所需要的时 间也相应的增加。进化终止条件指的是当进化到什么时候结束,它可以设定到某一代进 化结束,也可能根据找出近似最优是否满足精度要求来确定。表1列出了生物遗传概念 在遗传算法中的对应关系。 生物迪传概包 适者生存 算法停止时,最优目标值的解有最大的可能被留住 个体 染色体 解的编码 基因 解中每一分量的特征 适应性 适应度函数值 种群 根据适应度函数值选取的一组解 交配 通过交配原则产生一组新解的过形 变异 编的某一分量发生变化的过程 22模型及算法 我们用遗传算法研究3.1.2中的问题。 求解的遗传算法的参数设定如下: 种群大小:M=50 最大代数:G=1000 交义率:P。=1,交叉概率为1能保证种群的充分进化。 变异率:P.=0.1, 一般而言,变异发生的可能性较小 (1)编码策略 -277
-277- §2 遗传算法 2.1 遗传算法简介 遗传算法(Genetic Algorithms,简称 GA)是一种基于自然选择原理和自然遗传机 制的搜索(寻优)算法,它是模拟自然界中的生命进化机制,在人工系统中实现特定目 标的优化。遗传算法的实质是通过群体搜索技术,根据适者生存的原则逐代进化,最终 得到最优解或准最优解。它必须做以下操作:初始群体的产生、求每一个体的适应度、 根据适者生存的原则选择优良个体、被选出的优良个体两两配对,通过随机交叉其染色 体的基因并随机变异某些染色体的基因后生成下一代群体,按此方法使群体逐代进化, 直到满足进化终止条件。其实现方法如下: (1) 根据具体问题确定可行解域,确定一种编码方法,能用数值串或字符串表示 可行解域的每一解。 (2) 对每一解应有一个度量好坏的依据,它用一函数表示,叫做适应度函数,适 应度函数应为非负函数。 (3) 确定进化参数群体规模 M 、交叉概率 pc 、变异概率 pm 、进化终止条件。 为便于计算,一般来说,每一代群体的个体数目都取相等。群体规模越大、越容 易找到最优解,但由于受到计算机的运算能力的限制,群体规模越大,计算所需要的时 间也相应的增加。进化终止条件指的是当进化到什么时候结束,它可以设定到某一代进 化结束,也可能根据找出近似最优是否满足精度要求来确定。表 1 列出了生物遗传概念 在遗传算法中的对应关系。 表 2 生物遗传概念在遗传算法中的对应关系 生物遗传概念 遗传算法中的作用 适者生存 算法停止时,最优目标值的解有最大的可能被留住 个体 解 染色体 解的编码 基因 解中每一分量的特征 适应性 适应度函数值 种群 根据适应度函数值选取的一组解 交配 通过交配原则产生一组新解的过程 变异 编码的某一分量发生变化的过程 2.2 模型及算法 我们用遗传算法研究 3.1.2 中的问题。 求解的遗传算法的参数设定如下: 种群大小: M = 50 最大代数:G = 1000 交叉率: pc = 1,交叉概率为 1 能保证种群的充分进化。 变异率: pm = 0.1, 一般而言,变异发生的可能性较小。 (1) 编码策略