
9.1.1 Echo Cancelation in Communications Two Possible Ways 1.Design a compromise fired echo canceler based on some “average'”echo path(平均的抵消回声). 2.Design an adaptive echo canceler that can "learn"the echo path when it is first turned on and afterward "tracks"its variations without any intervention from the designer 应的抵消回声)·
Two Possible Ways 1. Design a compromise fixed echo canceler based on some “average” echo path(平均的抵消回声). 2. Design an adaptive echo canceler that can “learn” the echo path when it is first turned on and afterward “tracks” its variations without any intervention from the designer(自适 应的抵消回声). 9.1.1 Echo Cancelation in Communications

9.1.1 Echo Cancelation in Communications Echo canceler From talker A Hybrid B Speech Talker Echo from B B To talker A replica D Echo from 4 The adaptive filter attempts to estimate the path from C to D and then generate an echo replica for noise cancellation. In this way,the talkers can quarrel if they want t0. FIGURE 9.3 Principle of echo cancelation
9.1.1 Echo Cancelation in Communications FIGURE 9.3 Principle of echo cancelation The adaptive filter attempts to estimate the path from C to D and then generate an echo replica for noise cancellation. In this way, the talkers can quarrel if they want to
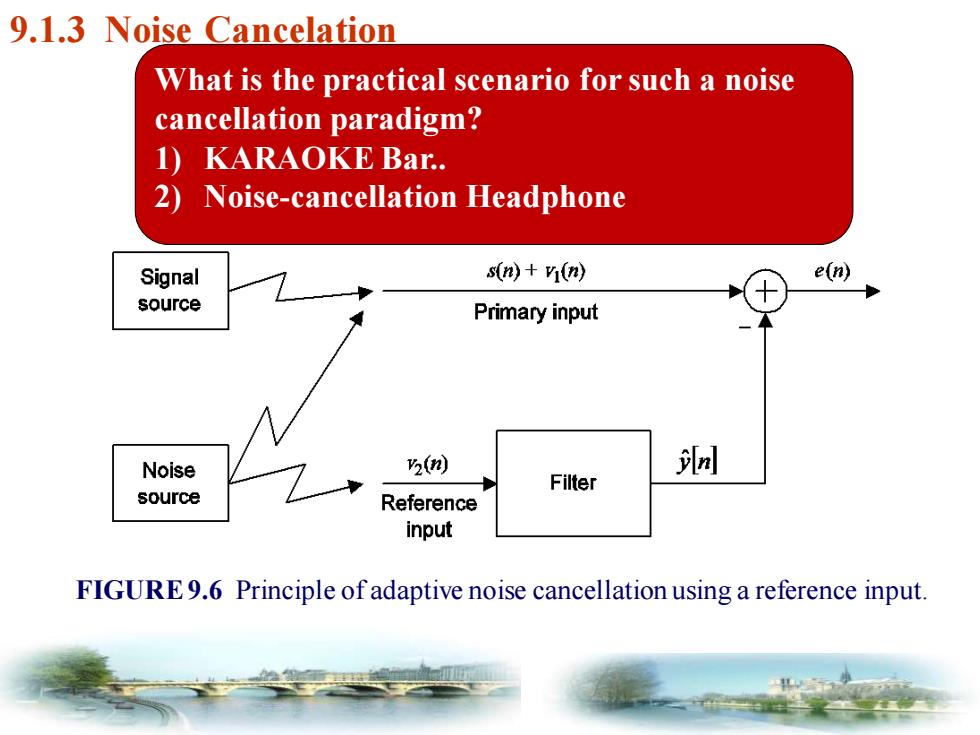
9.1.3 Noise Cancelation What is the practical scenario for such a noise cancellation paradigm? 1)KARAOKE Bar. 2)Noise-cancellation Headphone Signal s(n)+(n) e(n) source Primary input Noise 2物 Filter source Reference input FIGURE9.6 Principle of adaptive noise cancellation using a reference input
FIGURE 9.6 Principle of adaptive noise cancellation using a reference input. 9.1.3 Noise Cancelation What is the practical scenario for such a noise cancellation paradigm? 1) KARAOKE Bar. 2) Noise-cancellation Headphone
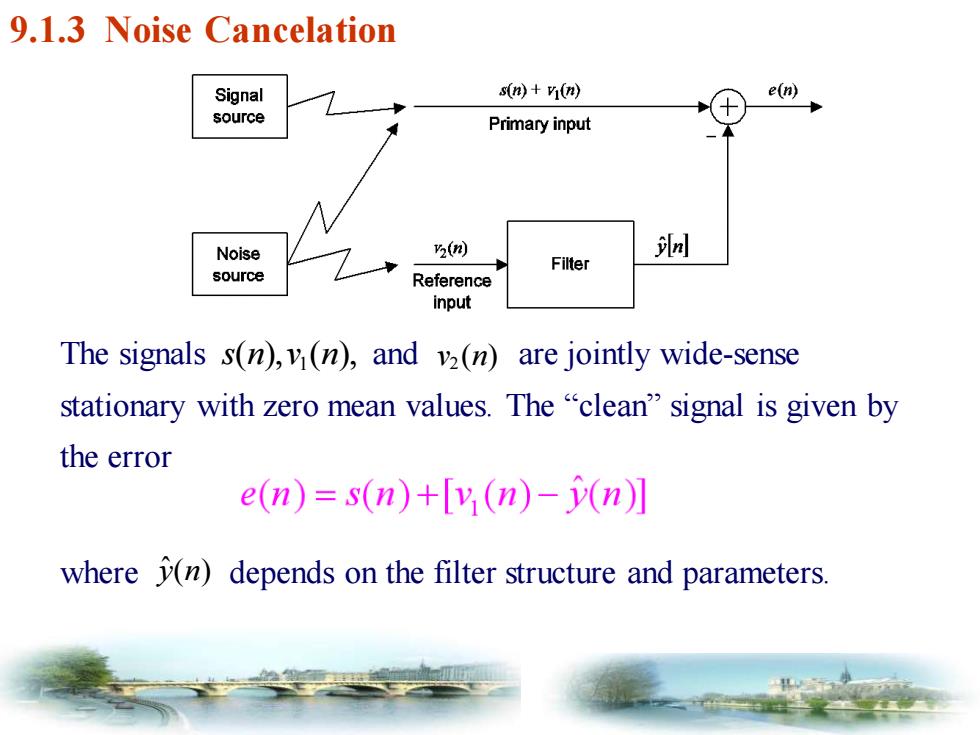
9.1.3 Noise Cancelation Signal s(n)+(n) e(n source Primary input Noise (倒 Filter source Reference input The signals s(n),v(n),and v2(n)are jointly wide-sense stationary with zero mean values.The"clean"signal is given by the error e(n)=s(n)+[y(n)-n)] where (n)depends on the filter structure and parameters
The signals and are jointly wide-sense stationary with zero mean values. The “clean” signal is given by the error s n v n ( ) ( ) 1 v n 2 ( ) where depends on the filter structure and parameters. y n ˆ( ) 9.1.3 Noise Cancelation
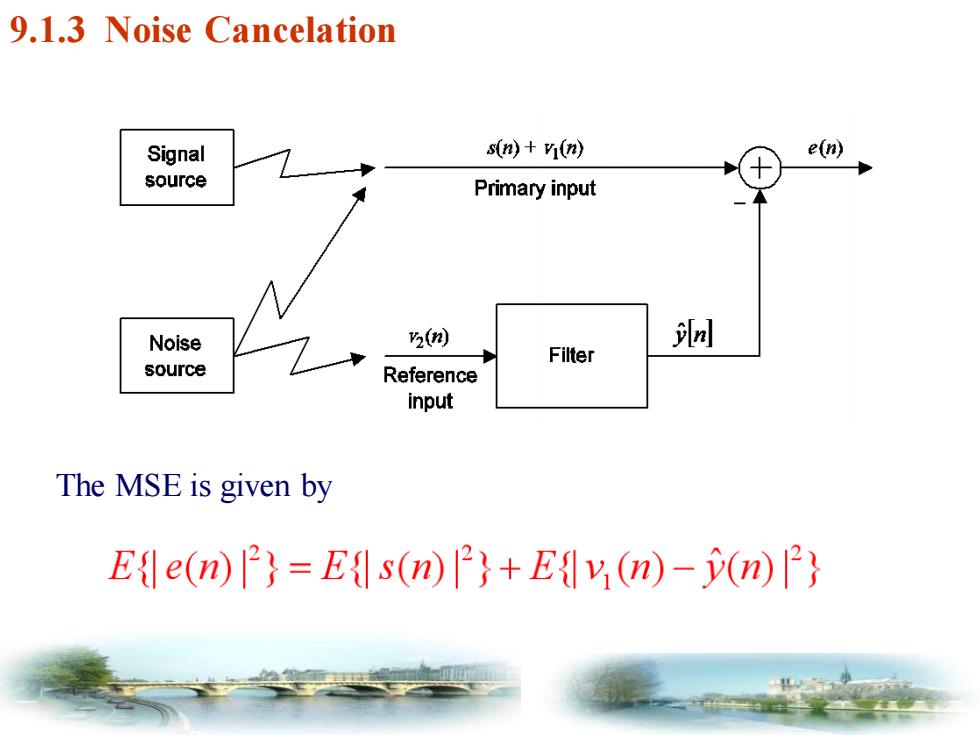
9.1.3 Noise Cancelation Signal (m)+y1(m) e(n) source Primary input Noise 2(例 Filter source Reference input The MSE is given by Ede(n)=Es(n)+Ev(n)-(n
The MSE is given by 9.1.3 Noise Cancelation