西安电子科技大学：《电路分析基础》课程教学课件（讲稿）第三章 动态电路

3动态元作 南感 对电感伏安关巢的微分形式从-∞到t进行积分，并设i(仁∞)=0，可得 称电感VAR的积分形 式 =2nu)a 设t=to为初始观察时刻，上式可改写为 0=25d5+2J(5d5=o)+2J5)d5 ,t≥t0 u与i 式中 i(to)= Iug)ds 非关 联 称为电感电流在to时刻的初始值，或初始状态，它包含了。 在t0以前电压的“全部历史”信息。一般取to=0。 u 若电感电压、电流的参考方向非关联，如右图所示。 电感VAR表达式可改为 d u(t)=- 0=45d=u)打45)d5 ,t之t0

西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 3-11 页 前一页 下一页 返回本章目录 3.1 动态元件    t u L i t ( ) d 1 称电感VAR的积分形 ( ) 式 设t=t0为初始观察时刻，上式可改写为          t t t t t u t t L u i t L u L i t 0 0 0 0 0 ( ) d , 1 ( ) d ( ) 1 ( ) d 1 ( )          0 ( ) d 1 ( ) 0 t u L i t   称为电感电流在t0时刻的初始值,或初始状态，它包含了 在t0以前电压的“全部历史”信息。一般取t0 =0 。 式中 若电感电压、电流的参考方向非关联，如右图所示。 电感VAR表达式可改为 u i L t i u t L d d ( )           t t t u t t L u i t L i t 0 0 0 ( ) d , 1 ( ) d ( ) 1 ( )     u与i 非关 联 对电感伏安关系的微分形式从-∞到t进行积分，并设i(-∞)=0，可得

3动态元佣 电感 3、电感的功率与储能 当电感电压和电流为关联方向时，电感吸收的瞬时功率为： p()=u)i(t)=1 di(Di(t) dt 电感是储能元件，它不消耗能量。当)>0时，说明电感是在吸 收能量，处于充磁状态；当()<0时，说明电感是在释放能量，处 于放磁状态。释放的能量总也不会超过吸收的能量。电感不能产生 能量，因此为无源元件。 对上式从一∞到t进行积分，即得t时刻电感上的储能为： w0=」p(5)a5=2(5d50 =号u20-}i2(-o ● 式中（∞）表示电感未充磁时刻的电流值，应有i(∞)=0。于是，电 感在时刻1的储能可简化为： w0=12(0 可见：电感在某一时刻1的储能仅取决于此时刻的电流，而与电压无 关，且储能≥0

西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 3、电感的功率与储能 第 3-12 页 前一页 下一页 返回本章目录 3.1 动态元件 当电感电压和电流为关联方向时，电感吸收的瞬时功率为： ( ) ( ) ( ) ( ) ( ) i t dt di t p t  u t i t  L 电感是储能元件，它不消耗能量。当 p(t)>0时，说明电感是在吸 收能量，处于充磁状态；当 p(t) <0时，说明电感是在释放能量，处 于放磁状态。释放的能量总也不会超过吸收的能量。电感不能产生 能量，因此为无源元件。 对上式从-∞到 t 进行积分，即得t 时刻电感上的储能为： ( ) 2 1 ( ) 2 1 ( ) ( ) ( ) ( ) 2 2 ( ) ( )          Li t Li w t p d Li di t i t i L     式中i(-∞) 表示电感未充磁时刻的电流值，应有i(-∞) =0。于是，电 感在时刻 t 的储能可简化为： ( ) 2 1 ( ) 2 wL t  Li t 可见：电感在某一时刻 t 的储能仅取决于此时刻的电流，而与电压无 关，且储能 ≥0

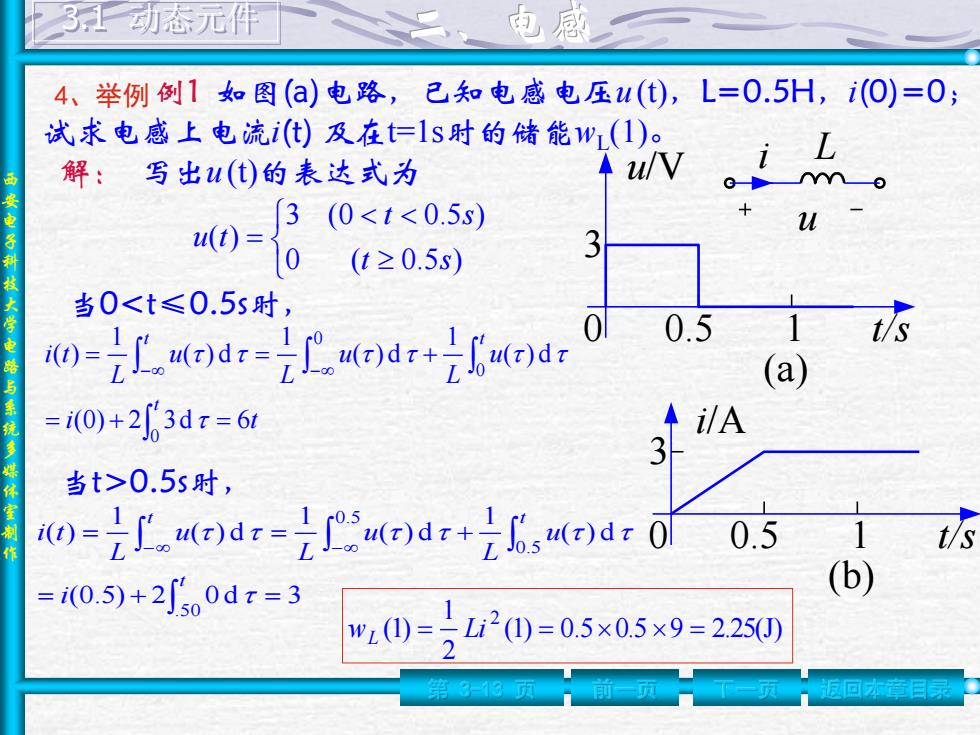
3上动态元作 南感 4、举例例1如图()电路，己知电感电压u(①)，L=0.5H,i(O)=0; 试求电感上电流i(t)及在=1s时的储能w(1)。 解：写出u()的表达式为 Au/V i L 0)= 3(0<t<0.5s) 3 0 (t≥0.5s) 0<t≤0.5s时， 0-7.0:dr*uga:0 0.5 1 (a) =i0)+23dx=61 当t>0.5s时， 0=2打。)dr=打r)dr+2,(rdr00.5 t/s =i0.5)+25o0dπ=3 (b) w(0=)20=05x05×9=2250

西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 4、举例 第 3-13 页 前一页 下一页 返回本章目录 3.1 动态元件 例1 如图(a)电路，已知电感电压u (t)，L=0.5H，i(0)=0； 试求电感上电流i(t) 及在t=1s时的储能wL (1)。 (a) u i L 0 t/s 3 u/V 0.5 1 解： 写出u (t)的表达式为        0 ( 0.5 ) 3 (0 0.5 ) ( ) t s t s u t 当0<t≤0.5s时， i t u L u L u L i t t t t (0) 2 3d 6 ( ) d 1 ( ) d 1 ( ) d 1 ( ) 0 0 0                     当t>0.5s时， (0.5) 2 0 d 3 ( ) d 1 ( ) d 1 ( ) d 1 ( ) .5 0 0.5 0.5             t t t i u L u L u L i t        (b) 0 t/s 3 i/A 0.5 1 (1) 0.5 0.5 9 2.25(J) 2 1 (1) 2 wL  Li    

31上动态元佣 电感 5、主要结论 (1)电感元件是动态元件。 (2)由电感VAR的微分形式可知：①任意时刻，通过电感的 电压与该时刻电流的变化率成正比。当电感电压山为有限 值时，其didt也为有限值，则电流i必定是连续函数，此时 电感电流是不会跃变的。②当电感电流为直流电流时，则 电压山=0，即电感对直流相当于短路。 (3)由电感VAR的积分形式可知：在任意时刻t,电感电流 是此时刻以前的电压作用的结果，它“记载”了以前电压 的“全部历史”。即电感电流具有“记忆”电压的作用， 故电感也是一个记忆元件。 (4)电感是一个储能元件，它从外部电路吸收的能量，以磁 场能量的形式储存于自身的磁场中。电感L在某一时刻的 储能只与该时刻t电感电流有关

西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 5、主要结论 第 3-14 页 前一页 下一页 返回本章目录 3.1 动态元件 （1）电感元件是动态元件。 （2）由电感VAR的微分形式可知：①任意时刻，通过电感的 电压与该时刻电流的变化率成正比。当电感电压 u为有限 值时，其di/dt也为有限值，则电流i必定是连续函数，此时 电感电流是不会跃变的。②当电感电流为直流电流时，则 电压 u = 0，即电感对直流相当于短路。 （3）由电感VAR的积分形式可知：在任意时刻t，电感电流i 是此时刻以前的电压作用的结果，它“记载”了以前电压 的“全部历史”。即电感电流具有“记忆”电压的作用， 故电感也是一个记忆元件。 （4）电感是一个储能元件，它从外部电路吸收的能量，以磁 场能量的形式储存于自身的磁场中。电感L在某一时刻的 储能只与该时刻t电感电流有关

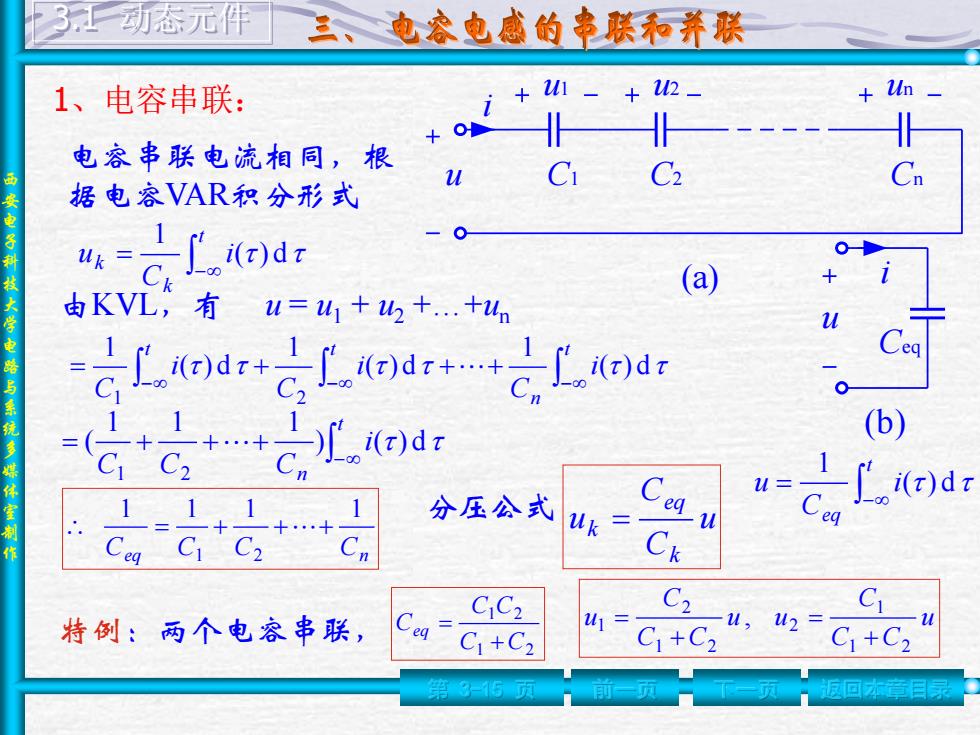
3动态元佣 三、电容电感的串联和并联 1、电容串联： 1-+2 +ln +O 电容串联电流相同，根 Ci C2 Cn 据电容VAR积分形式 (a) 由KVL,有u=41++..+un i)dtc)d C.L.K)dr 1 (b) C> u= 分压公式 )dr uk= eq C Ck C2 特例：两个电容串联， eg- C1+C2 C1+C2 C1+C2

西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 1、电容串联： 第 3-15 页 前一页 下一页 返回本章目录 3.1 动态元件 u1 u2 un u i (a) C1 C2 Cn Ceq u i (b) 电容串联电流相同，根 据电容VAR积分形式    t k k i C u ( ) d 1 由KVL，有 u = u1 + u2 +…+un           t n t t i C i C i C     ( ) d 1 ( ) d 1 ( ) d 1 1 2        t n i C C C ) ( ) d 1 1 1 ( 1 2  Ceq C C Cn 1 1 1 1 1 2     分压公式 u C C u k eq k  特例：两个电容串联， 1 2 1 2 C C C C Ceq   u C C C u u C C C u 1 2 1 2 1 2 2 1 ,        t eq i C u ( ) d 1