一动态元佣 电容 4、举例例1如图()电路,电源电压s(①)如图(b);试求电容 上电流()、縣时功率p()及在t时刻的储能wc(①)。 us! 解:写出us()的表达式为 0,t<0 t,0<t<1s us(t)= (t-2),1<t<2s ◆(t)/A p(t)/W b 0,t>2s 根据电容VAR得 吸收能量 0,t<0 )=2ds 2,0<f<1s dt -2,1<1<2s 释放能量 0,t>2s (d) wc(t)/J 0,t<0 0,1<0 2t,0<t<ls p(t)=us(1)i(t)= t2,0<t<1s 2t-2),1<1<2swc(0=C2(0= 人 0,t>2s u-22,1<1<2s01、 2认s 0,t>2s
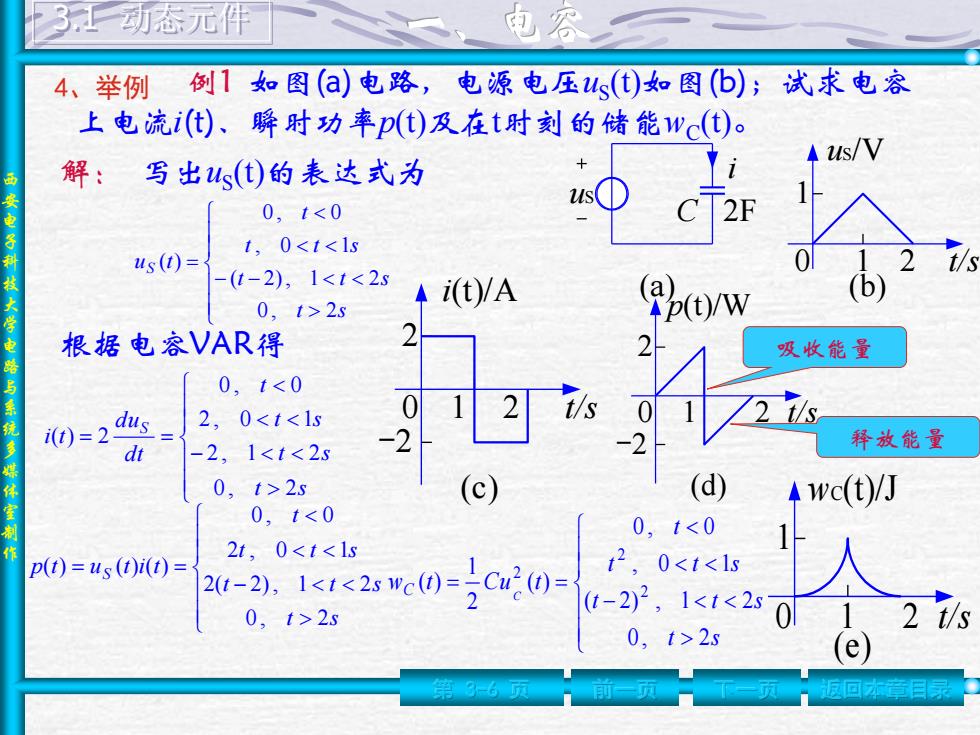
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 4、举例 第 3-6 页 前一页 下一页 返回本章目录 3.1 动态元件 例1 如图(a)电路,电源电压uS (t)如图(b);试求电容 上电流i(t)、瞬时功率p(t)及在t时刻的储能wC (t)。 uS C 2F i (a) uS/V 0 t/s 1 1 2 (b) 解: 写出uS (t)的表达式为 t s t t s t t s t u t S 0 , 2 ( 2), 1 2 , 0 1 0 , 0 ( ) 根据电容VAR得 t s t s t s t dt du i t S 0 , 2 2 , 1 2 2 , 0 1 0 , 0 ( ) 2 i(t)/A 0 t/s 2 1 2 (c) -2 t s t t s t t s t p t u t i t S 0 , 2 2( 2), 1 2 2 , 0 1 0 , 0 ( ) ( ) ( ) p(t)/W 0 t/s 2 1 2 (d) -2 t s t t s t t s t w t Cu t C C 0 , 2 ( 2) , 1 2 , 0 1 0 , 0 ( ) 2 1 ( ) 2 2 2 wC(t)/J 0 t/s 1 1 2 (e) 吸收能量 释放能量

3动态元佣 例2某电容C=2F,其电流波形如图所示。 Ai/A ①若(0)=0,求电容电压u(),t≥0 8 ②计算t=2s时电容的储能w(2)。 4 解:电容电流的表达式为: 4/小 0,t<0 ↑u/V 8,0<t<1s 6 i(t)= 0,1<t<3s 4,3<1<4s 0,t>4 0 1234/ ,t≤0 根据电容VAR得 zfosdr-4 ,0<1≤1s 0=0)+2J(o)dr 2J8dr+打bdr=0+0=4 ,1<t≤3s 8)+号4dr=4+20-3)=20-0,3<1≤4 w(2)=C2(2)=16J 4+J0ar=4=6 t>4
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 例2 某电容C=2F,其电流i波形如图所示。 ①若u(0)=0,求电容电压u(t),t≥0 ②计算t=2s时电容的储能w(2)。 第 3-7 页 前一页 下一页 返回本章目录 3.1 动态元件 解: 电容电流的表达式为: 0 , 4 4 , 3 4 0 , 1 3 8, 0 1 0 , 0 ( ) t t s t s t s t i t 根据电容VAR得 0 d (4) 6 4 2 1 (4) 4 d 4 2( 3) 2( 1) ,3 4 2 1 (3) 0 d (1) 0 4 ,1 3 2 1 8 d 2 1 8 d 4 ,0 1 2 1 0 , 0 ( ) d 1 ( ) (0) 4 3 1 0 1 0 0 u u t u t t t s u t s t t s t i C u t u t t t t t 0 t/s 4 6 u/V 1 2 3 4 u i C 0 t/s 4 8 i/A 1 2 3 4 w Cu (2) 16J 2 1 (2) 2

3动态元佣 南 5、主要结论 (们)电容的伏安关系是微积分关条,因此电容元件是动态元件。而电阻 元件的伏安关系是代数关系,电阻是一个即时(瞬时)元件。 (2)由电容VAR的微分形式可知:①任意时刻,通过电容的电流与该时 刻电压的变化率成正比。当电容电流为有限值时,其dldt也为有限 值,则电压山必定是连续函数,此时电容电压是不会跃变的。②当电容 电压为直流电压时,则电流=0,此时电容相当于开路,故电容有隔 直流的作用。 (3)由电容VAR的积分形式可知:在任意时刻t,电容电压u是此时刻以 前的电流作用的结果,它“记载”了以前电流的“全部历史”。即电 容电压具有“记忆”电流的作用,故电容是一个记忆元件,而电阻是 无记忆元件。 (4)电容是一个储能元件,它从外部电路吸收的能量,以电场能量的形 式储存于自身的电场中。电容C在某一时刻的储能只与该时刻t电容电 压有关
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 3.1 动态元件 5、主要结论 第 3-8 页 前一页 下一页 返回本章目录 (1)电容的伏安关系是微积分关系,因此电容元件是动态元件。而电阻 元件的伏安关系是代数关系,电阻是一个即时(瞬时)元件。 (2)由电容VAR的微分形式可知:①任意时刻,通过电容的电流与该时 刻电压的变化率成正比。当电容电流 i为有限值时,其du/dt也为有限 值,则电压u必定是连续函数,此时电容电压是不会跃变的。②当电容 电压为直流电压时,则电流 i = 0,此时电容相当于开路,故电容有隔 直流的作用。 (3)由电容VAR的积分形式可知:在任意时刻t,电容电压u是此时刻以 前的电流作用的结果,它“记载”了以前电流的“全部历史”。即电 容电压具有“记忆”电流的作用,故电容是一个记忆元件,而电阻是 无记忆元件。 (4)电容是一个储能元件,它从外部电路吸收的能量,以电场能量的形 式储存于自身的电场中。电容C在某一时刻的储能只与该时刻t电容电 压有关
3动态元佣 将导线绕在骨架上就构成一个实际电感线圈 Kt) (也称电感器),如图(a)。 电感元件(inductor)是一种储存磁能的元件。 (t) 平(t) 它是实际电感线圈的理想化模型,其电路待号 如图(b)所示。 当电流()通过线圈时,将产生磁通Φ(t),其 (a) 中储存有磁场能量。与线圈交链的总磁通称为 磁链Ψ()。若线圈密绕,且有N匝,则磁链 i(t)L(t) Ψ(t)=NΦ(t)。 十 u(t) 1、电感的一般定义 (b) 一个二端元件,若在任一时刻t,其磁链Ψ(什)与电流(t)之 问的关系能用Ψ~平面上的曲线表征,即具有代数关华f(Ψ )=0,则称该元件为电感元件,简称电感
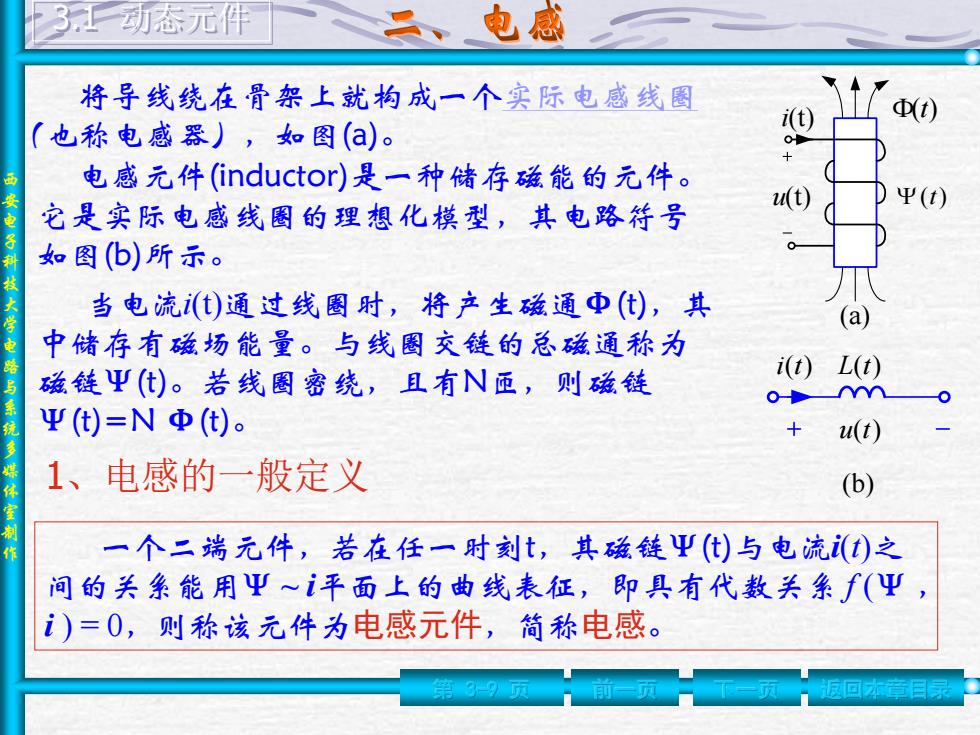
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 3-9 页 前一页 下一页 返回本章目录 3.1 动态元件 将导线绕在骨架上就构成一个实际电感线圈 (也称电感器),如图(a)。 (b) i(t) L(t) u(t) 当电流i(t)通过线圈时,将产生磁通Φ(t),其 中储存有磁场能量。与线圈交链的总磁通称为 磁链Ψ(t)。若线圈密绕,且有N匝,则磁链 Ψ(t)=N Φ(t)。 1、电感的一般定义 一个二端元件,若在任一时刻t,其磁链Ψ(t)与电流i(t)之 间的关系能用Ψ ~ i平面上的曲线表征,即具有代数关系 f (Ψ , i ) = 0,则称该元件为电感元件,简称电感。 电感元件(inductor)是一种储存磁能的元件。 它是实际电感线圈的理想化模型,其电路符号 如图(b)所示。 i(t) u(t) (a) (t) (t)
1动态元 电感 电感也分:时变和时不变的,线性的和非线性的。 线性时不变电感的外特性(韦安特性)是Ψ平面上一条过原点的直线, 且其斜率L不随时间变化,如图()所示。其表达式可写为: )=L() 其中L就是电感元件的值,单位为:亨[利](H)。磁链的 单位:韦[伯](Wb)。对于线性时不变电感,L为正实常数。 2、电感的VAR(或VCR) 电感中,古电流变化时,磁链也发生变化,从而产生感应电压。在电流 与电压券考方向关联时,若电压参考文向与强通的方向陆合右手法则餐提 法拉第电磁感应定律,感应电压()与磁链的变化率成正比,即:()= dt 对线性电感,由于()=L(t),故有 )= di dt u(t) 称电感VAR的微分形式 (b)
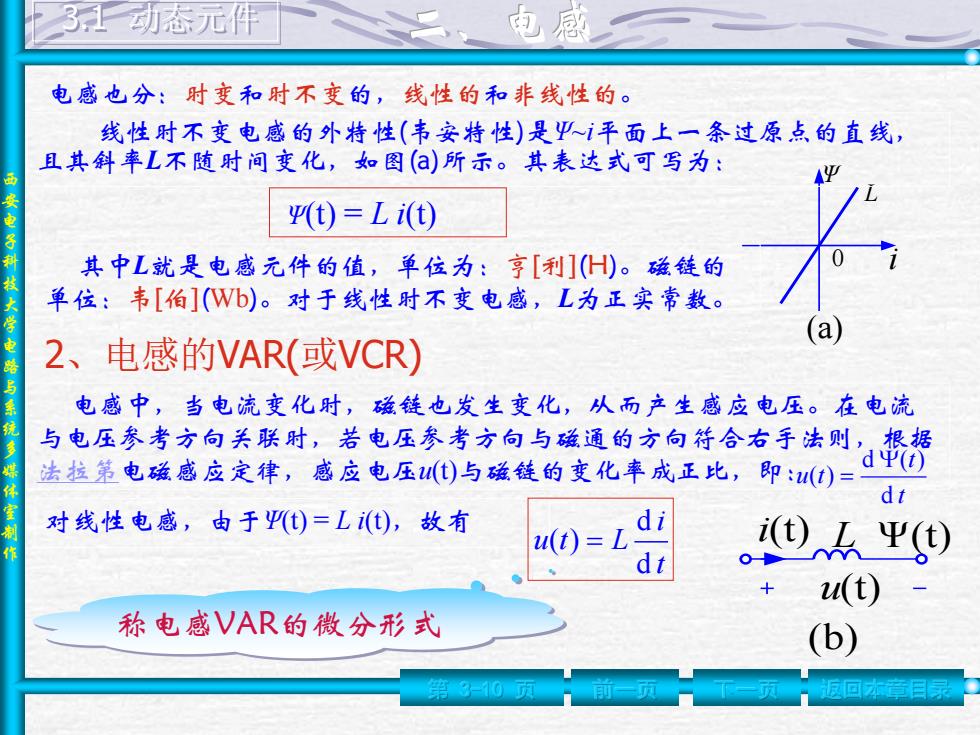
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 3-10 页 前一页 下一页 返回本章目录 3.1 动态元件 (a) Ψ 0 i L 线性时不变电感的外特性(韦安特性)是Ψ~i平面上一条过原点的直线, 且其斜率L不随时间变化,如图(a)所示。其表达式可写为: Ψ(t) = L i(t) 其中L就是电感元件的值,单位为:亨[利](H)。磁链的 单位:韦[伯](Wb)。对于线性时不变电感,L为正实常数。 2、电感的VAR(或VCR) 电感中,当电流变化时,磁链也发生变化,从而产生感应电压。在电流 与电压参考方向关联时,若电压参考方向与磁通的方向符合右手法则,根据 法拉第电磁感应定律,感应电压u(t)与磁链的变化率成正比,即: t t u t d d ( ) ( ) (b) i(t) Ψ(t) u(t) L 对线性电感,由于Ψ(t) = L i(t),故有 t i u t L d d ( ) 称电感VAR的微分形式 电感也分:时变和时不变的,线性的和非线性的