
Three dimensional ES barrier E3D-0.16 eV result in islands E3D-0.40 eV result in nanorods with lateral dimension 1000 nm diameter of~100 nm. L.G.Zhou,et.al.Phys.Revie Lett.101,266102(2008)
E3D=0.16 eV result in islands with lateral dimension 1000 nm E3D=0.40 eV result in nanorods diameter of ~100 nm. L. G. Zhou, et. al. Phys. Revie Lett. 101, 266102 (2008). Three dimensional ES barrier

Nanorod?Two length-scales Advantages Advantages Catalytic Activity Increased Surface Area Surface Plasmon Resonance Decreased Melting Temp Increased Strength In/decreased Thermal Conductivity ~100+nm ~10nm In/decreased Electrical Conductivity How small can the nanorod be?
Nanorod? Two length-scales ~100 + nm ~10 nm How small can the nanorod be? Advantages Increased Surface Area Advantages Catalytic Activity Surface Plasmon Resonance Decreased Melting Temp Increased Strength In/decreased Thermal Conductivity In/decreased Electrical Conductivity
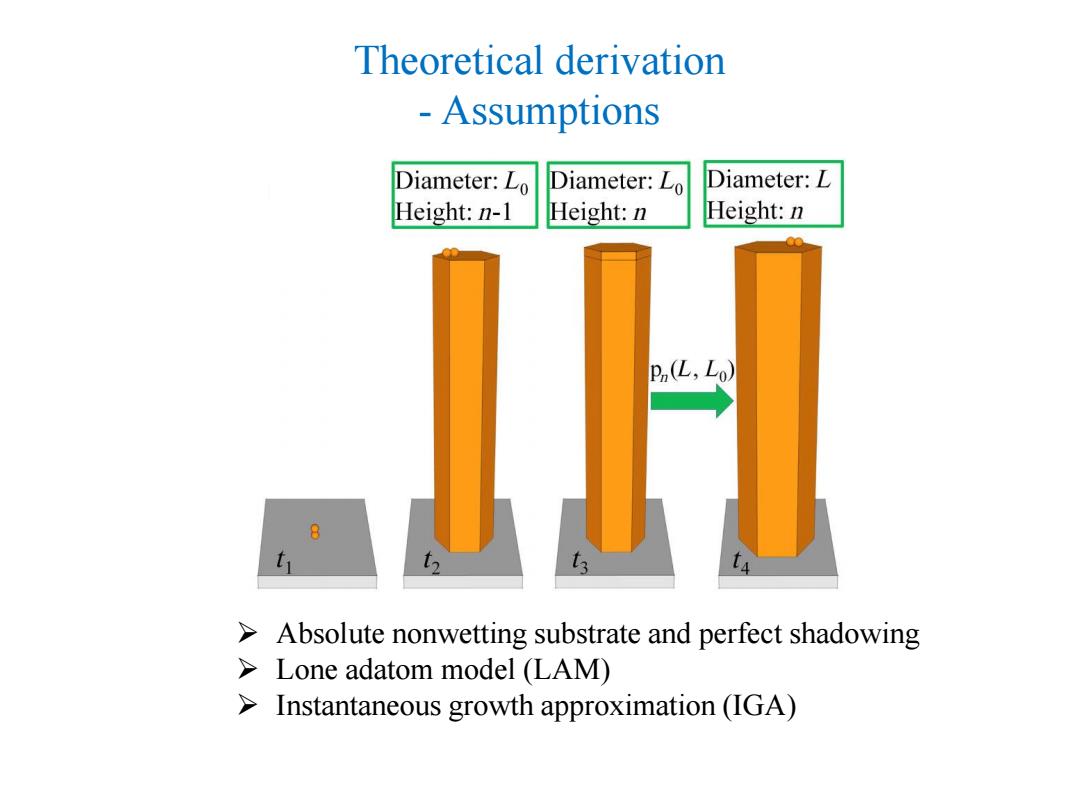
Theoretical derivation Assumptions Diameter:Lo Diameter:Lo Diameter:L Height:n-1 Height:n Height:n P(L,Lo) 8 > Absolute nonwetting substrate and perfect shadowing Lone adatom model (LAM) Instantaneous growth approximation(IGA)
Theoretical derivation - Assumptions ➢ Absolute nonwetting substrate and perfect shadowing ➢ Lone adatom model (LAM) ➢ Instantaneous growth approximation (IGA)

Theoretical derivation three-step approach >Objective:find the size distribution S(L)of nanorods with n-layer hight,right before the nucleation of the next layer >First step,assume that s(L)=(L),and derive S,(L) >Second step,we take the distribution S(L)into account to derive S(L)in the recursive form. > Third step,use the non-wetting condition to determine S(L),so as to derive the explicit expression ofS,(L).The peak value L of the size distribution S,(L)is the minimum size Lmin of nanorod with height n-layer. The lateral size of nanorod is L,the cross-section area 4=aL2 and perimeter C=4aL,with a=/4 for circular cross-section and a=1 for square cross-section
Theoretical derivation - three-step approach ➢ Objective: find the size distribution Sn (L) of nanorods with n-layer hight, right before the nucleation of the next layer ➢ First step, assume that , and derive Sn (L). ➢ Second step, we take the distribution Sn-1 (L) into account to derive Sn (L) in the recursive form. ➢ Third step, use the non-wetting condition to determine S1 (L), so as to derive the explicit expression of Sn (L). The peak value Lpn of the size distribution Sn (L) is the minimum size Lmin of nanorod with height n-layer. ➢ The lateral size of nanorod is L, the cross-section area A=αL 2 and perimeter C=4αL, with α=π/4 for circular cross-section and α=1 for square cross-section. S L L L n−1 0 ( ) = − ( )

Theoretical derivation-first step Lo L n- Time >All nanorods of n-layer high are in size Lo.Before nucleation takes place,the growth law is:Fadi=nanex(F2n) According to LAM,the nucleation rate AV3D >The fraction of nanorods on top of which nucleation has taken place are: f(L,4)=l-exp(dho=l-exp[((-)/匹]wihL.=[(uoro/aaF] 之ens.--爱o59 >p(L,Lo)dl represents the probability of nanorod,which have size within [L, Hdl]and which have nuclei on top.p(L,Lo)is also the size distribution S,(L) if Sm-1(L)=δ(L-Lo)
Theoretical derivation - first step ➢ All nanorods of n-layer high are in size L0 . Before nucleation takes place, the growth law is: ➢ According to LAM, the nucleation rate: ➢ The fraction of nanorods on top of which nucleation has taken place are: ➢ The probability density ➢ pn (L, L0 )dl represents the probability of nanorod, which have size within [l, l+dl] and which have nuclei on top. pn (L, L0 ) is also the size distribution Sn (L) if . 2 2 2 0 0 0 exp( 2 ) t F L dt n L n L L L Ft n = − = 2 2 5 3 4 R D D F L FA = = ( ) ( ) ( ) ( ) ( ) 1 5 5 5 5 2 0 0 3 0 , 1 exp 1 exp with 10 t n n n D f L L dt L L L L n F = − − = − − = ( ) ( ) 4 5 5 0 0 0 5 5 , 5 , exp n n n n df L L L L L p L L dL L L − = = S L L L n−1 0 ( ) = − ( ) n-1 L0 n L0 n L Time