电子科技大学：《材料设计与计算 Materials Design and Computation》课程教学资源（课件讲稿）MDC 14 Modeling and Simulation in Epitaxial Growth

Theoretical derivation-second step n- Time >By considering the size distribution S,(L)of nanorods of(n-1)-layer high S,()=dSn1(0)p.(L,1)

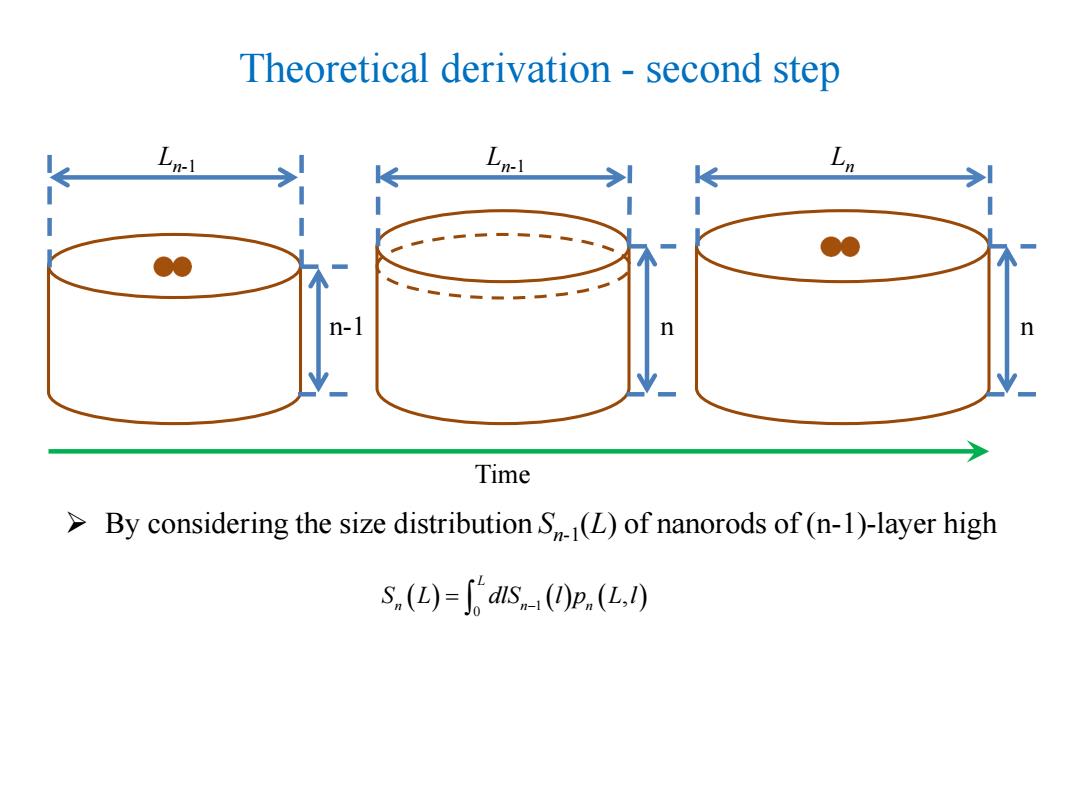
Theoretical derivation - second step ➢ By considering the size distribution Sn-1 (L) of nanorods of (n-1)-layer high n-1 Ln-1 n Ln-1 n Ln Time ( ) 1 ( ) ( ) 0 , L n n n S L dlS l p L l =  −

Theoretical derivation -third step >For non-wetting substrate,we assume that s(L)=5(L-0) s-u小-2om盖} 2 .()-.r.(n-on >To determine the peak size L that satisfies ds,(L)/dL=0 会- Lpm represents the size of nanorods that areon absolute non-wetting substrate, fully bounded by multiple-layer steps and perfect geometrical shadowing. Therefore,It is the theoretical lower limit of the diameter 4-[2]

Theoretical derivation - third step ➢ For non-wetting substrate, we assume that ➢ Thus we have ➢ To determine the peak size Lpn that satisfies ➢ Lpn represents the size of nanorods that areon absolute non-wetting substrate, fully bounded by multiple-layer steps and perfect geometrical shadowing. Therefore, It is the theoretical lower limit of the diameter S L L 1 ( ) = −  ( 0) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 4 5 5 5 4 2 2 5 5 5 5 5 2 2 2 2 2 3 2 4 5 5 3 2 3 5 5 5 0 2 2 2 5 5 2 1 2 exp exp exp 1 2 2 5 3 1 3 3 , = exp exp 1 2 2 2 L L L L L L S L p L L L L L L L L L S L dlS l p L l L L L − −       − − −   = = = −                 −     −   = −              ( ) ( ) ( ) ( ) 2 4 5 5 1 5 5 5 0 2 2 2 5 1 , = exp exp 1 2 2 2 n L n n n n nL nL L S L dlS l p L l L L L − − −     −   == −              ( ) 0 n dS L dL = 5 5 5 2 5 5 5 2 2 5 2 2ln 10 2 pn pn pn L nL L L L L   + =     +   1 1 5 5 3 min 2 2 10 2ln ln 2 2 n n D L L F            =                