
电波传播概论 Xidian University r×(nl)=常矢量 讨论: 1、在射线的每一点上,rX(nl)这个矢量 的方向都相同,也即r和lw所在平面的取向 不变,因此射线是平面曲线; 2、rX(nlo)的绝对值在射线上等于常数, 即 rsin⑩=const p是从地心引出的夫径与射线的夹角,也即 是射线的天顶角。 通常习惯于使用射线的仰角0,显然8三力 所以有 nrcos const 物理与光电工程学院电波传播研究所 西安电子科技大学
物理与光电工程学院电波传播研究所 西安电子科技大学 电波传播概论 0 r nl = ( ) 常矢量 讨论: 1、 在射线的每一点上, r×(nl0 ) 这个矢量 的方向都相同, 也即r和l0所在平面的取向 不变, 因此射线是平面曲线; 2、r×(nl0 )的绝对值在射线上等于常数, 即 nrsin const = φ是从地心引出的矢径r与射线的夹角, 也即 是射线的天顶角。 通常习惯于使用射线的仰角θ,显然 π 2 = − 所以有 nrcos const =

电波传播概论 Xidian University nrcos const +0+t行 2 +8+ 假设在射线的初始出发,点的折射 指数为o,射线的仰角为0,初始 出发点至地心的距离为ro=a+h, 一射线 则 n+dn nrcose norcose 地面 dd. 球面分层大气的斯奈尔定律 如果球面的半径为无限大,也即球 面退化成平面,此时rro=1+h/r≈1。 则平面分层情况下的折射公式,即 ncos0 ncose 物理与光电工程学院电波传播研究所 西安电子科技大学
物理与光电工程学院电波传播研究所 西安电子科技大学 电波传播概论 nrcos const = 假设在射线的初始出发点的折射 指数为n0 , 射线的仰角为θ0 , 初始 出发点至地心的距离为r0=a+hs , 则 0 0 0 nrcos n r cos = ——球面分层大气的斯奈尔定律 如果球面的半径为无限大, 也即球 面退化成平面, 此时r/r0=1+h/r0≈1。 则平面分层情况下的折射公式,即 0 0 ncos n cos =

电波传播概论 Xidian University 射线描迹 +0+ 2 +8+p 为了清楚地描述射线的轨道,在 已知,ro,c0s0的情况下,可用 射线 地面上的距离d和高度h的函数关 n十dn 系代表射线的轨迹方程。 一组d和h的数据可以惟一地确定 地面 dd 射线上对应点的位置。 在射线上,令点Q的相应坐标是d ! 和h,由点Q移动到P点时,相应的 半径r和高度h的变化为 dr dh tane rdp 物理与光电工程学院电波传播研究所 西安电子科技大学
物理与光电工程学院电波传播研究所 西安电子科技大学 电波传播概论 射线描迹 为了清楚地描述射线的轨道, 在 已知n0 , r0 , cosθ0的情况下, 可用 地面上的距离d和高度h的函数关 系代表射线的轨迹方程。 一组d和h的数据可以惟一地确定 射线上对应点的位置。 在射线上, 令点Q的相应坐标是d 和h, 由点Q移动到P点时, 相应的 半径r和高度h的变化为 dr dh tan rd = = ·

电波传播概论 Xidian University dr dh tane rdo +0+t行 +8+g 其中,dφ为地心张角的变化 2 do=dd Ir 一射线 dd为地面距离d的变化,将其代 n+dn 入上式,并考虑r=r+h,可得 地面 dd cote dd dh 1+h/ 01= 将上式积分,便得到对于高度h, 射线在地面上的投影距离d为 cot O dh 1+h/ 物理与光电工程学院电波传播研究所 西安电子科技大学
物理与光电工程学院电波传播研究所 西安电子科技大学 电波传播概论 其中,dφ为地心张角的变化 dr dh tan rd = = · 0 d dd r = / dd为地面距离d的变化,将其代 入上式,并考虑r=r0+h,可得 0 cot d d 1 / d h h r = + 将上式积分, 便得到对于高度ht , 射线在地面上的投影距离d为 t 0 0 cot d 1 / h d h h r = +
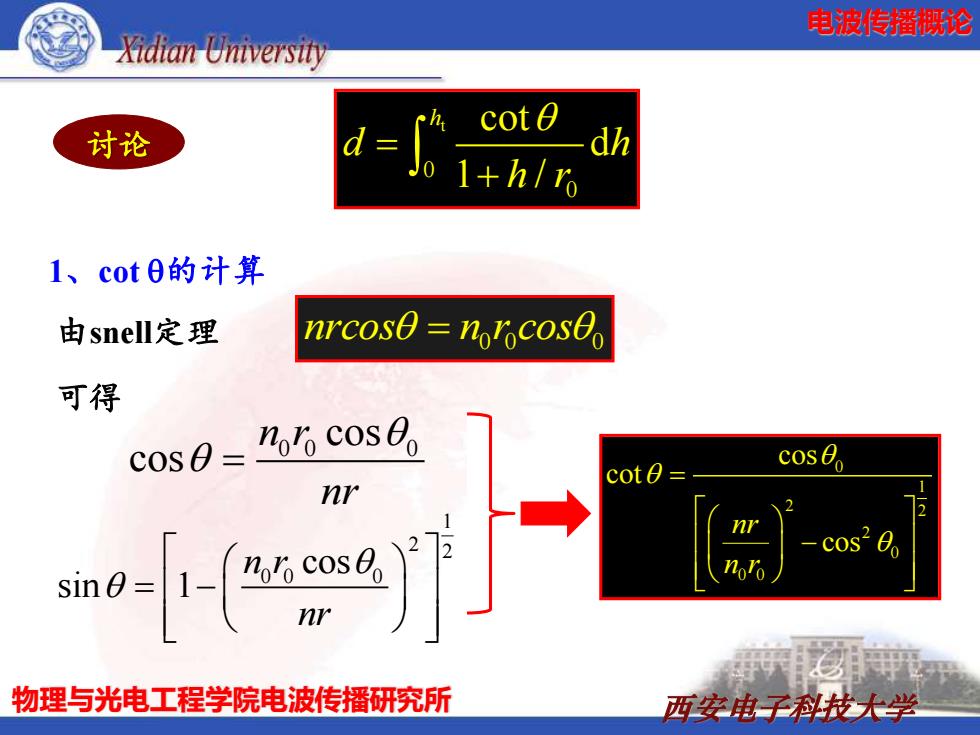
电波传播概论 Xidian University cot 0 讨论 dh 1+h/r 1、cot0的计算 由snell定理 nrcose norcose 可得 cos0=n6cos0。 cosθ cot nr e cos2 0 noro 物理与光电工程学院电波传播研究所 西安电子科技大学
物理与光电工程学院电波传播研究所 西安电子科技大学 电波传播概论 t 0 0 cot d 1 / h d h h r = + 讨论 1、cot 的计算 0 0 0 由snell定理 nrcos n r cos = 可得 0 0 0 cos cos n r nr = 1 2 2 0 0 0 cos sin 1 n r nr = − 0 1 2 2 2 0 0 0 cos cot cos nr n r = −