
效用则是消费者在消费一定量的商品时所累计得到的所有的边际效用的总和。 比如,消费量为5个单位的总效用,是第一致第五单位商品的边际效用之和, 即5+4+3+2+1=15(效用单位)。 表4.1里的数字可以用图4.1表示。 图4.1总效用曲线和边际效用曲线 在图4.1中,横轴OQ表示商品消费量,纵轴TU和MU分别表示总效用 量和边际效用量。当物品的消费量可以无限地细分时,我们可以绘出总效用曲 线和边际效用曲线。从图(b)可以看出,边际效用曲线是向右下方倾斜的,斜 率为负,显示出边际效用的递减性。由前面讲过的MW=T巴可知,总效用曲 do 线上任一点的斜率,即是该点的边际效用的数值。边际效用的递减性表明。图 (a)中的总效用曲线必然是倒“U”型的(或“I”型的)。换句话说,当商 品的边际效用递减但为正值时,总效用以递减的速度增加;当边际效用为零时, 总效用达到最大值:当边际效用为负时,总效用开始下降。 四、消费者均衡 作为理性的消费者,他在运用有限的货币收入购买商品时,总是希望获得 最大程度的满足,实现效用最大化。消费者均衡是指在商品价格和消费者收入 既定的情况下,消费者实现效用最大化时不愿变动任何商品购买数量的一种相 对静止状态。比如,某大学生带了500元现金上街购物,而对琳琅满目的商品, 他的脑海中涌现出多种购买方案,最后他决定用这500元购买三本书、一台收 录机和一件克衫。此时他不再变更其购买方案,一定是因为这一方案能给他带 来了大程度的满足,这时我们说大学实现了效用最大化,或者说处于消费者均 衡状态。 消费者怎样才能实现效用最大化呢?我们可以用公式说明该问题。假设消 费者可以对几种商品进行选择,其价格分别以P、P2…P。来表示,数量分别 以Q1、Q2…Qn表示,商品边际效用分别以MU、MU2…MUn表示,消费者 的货币收入为I,一个单位货币的边际效用为常数入①。则消费者实现效用最 大人的条件可以用公式表示为: PQ1+PQ2+…+PQ。=l (4.4) MU=MU2=A MUm=入 (4.5) 卫P2 P (4.4)式为消费者实现效用最大化的约束条件。它要求,在商品价格和 消费者收入既定的条件下,消费者把全部收入都用于购买各种商品,既无储蓄 现象,也无负债进行消费的行为

(4.5)式为消费者实现效用最大化的均衡条件。它表明,当各种商品的 边际效用与其价格之比相等时,消费者可以实现效用最大化。 ①基数效用记者认为,货币如同商品一样具有效用,且其边际效用是递减 的。但是,在分析消费者行为时,他们假定货币的边际效用是一个不变的常数。 其理由是,在商品价格只在消费者收入中占有很小比例的情况下,商品购买量 的连续变化,只会导致消费者的货币收入发生很小的变化,从而使货币的边际 效用发生微小的可以忽略不计的变化。或当花费在任何一种物品上的最后一单 位货币所带来的边际效用都相等时,消费者可以实现效用最大化。这一条件又 被称作等边际原则(Equimarginal Principle)。 如果消费者所购买的是X与Y两种商品,则消费者实现效用最大化的条件 可以表示为: PxOx+PyOy =I (4.6) MUx MUy (4.7) Px Py 为什么消费者必须按等边原则购买商品,才可实现效用最大化呢?我们以 消费者选择两种商品的情况为例进行说明。 假设某消费者在对苹果(X商品)与牛肉(Y商品)进行选择时,最初的 所带来的边际效用不相等,即M大于小或小于M心 Px Py 当M>M心时,表明消费者花在X商品即苹果上的最后一单位货币所 Px Py 带来的边际效用超过花在牛肉上的最后一单位货币带给他的边际效用,为了实 现效用的最大化,理性的消费者必然会增加对X商品即苹果的购买量,减少对 牛肉的购买量。根据边际效用递减规律,随着苹果购买量的增加,苹果的边际 效用下降,使得M匹的数值减小,而随着牛肉购买量的减少:牛肉的边际效用 Px 增加,使得M心的数值增大。这样,消费者对购买数量的调整,会使Mr与 Py Px M少之间的差距越来越越小,最终会趋于相等。 同理,当M<M心时,消费者减少对x商品即苹果的购买量,增加对 Px Py
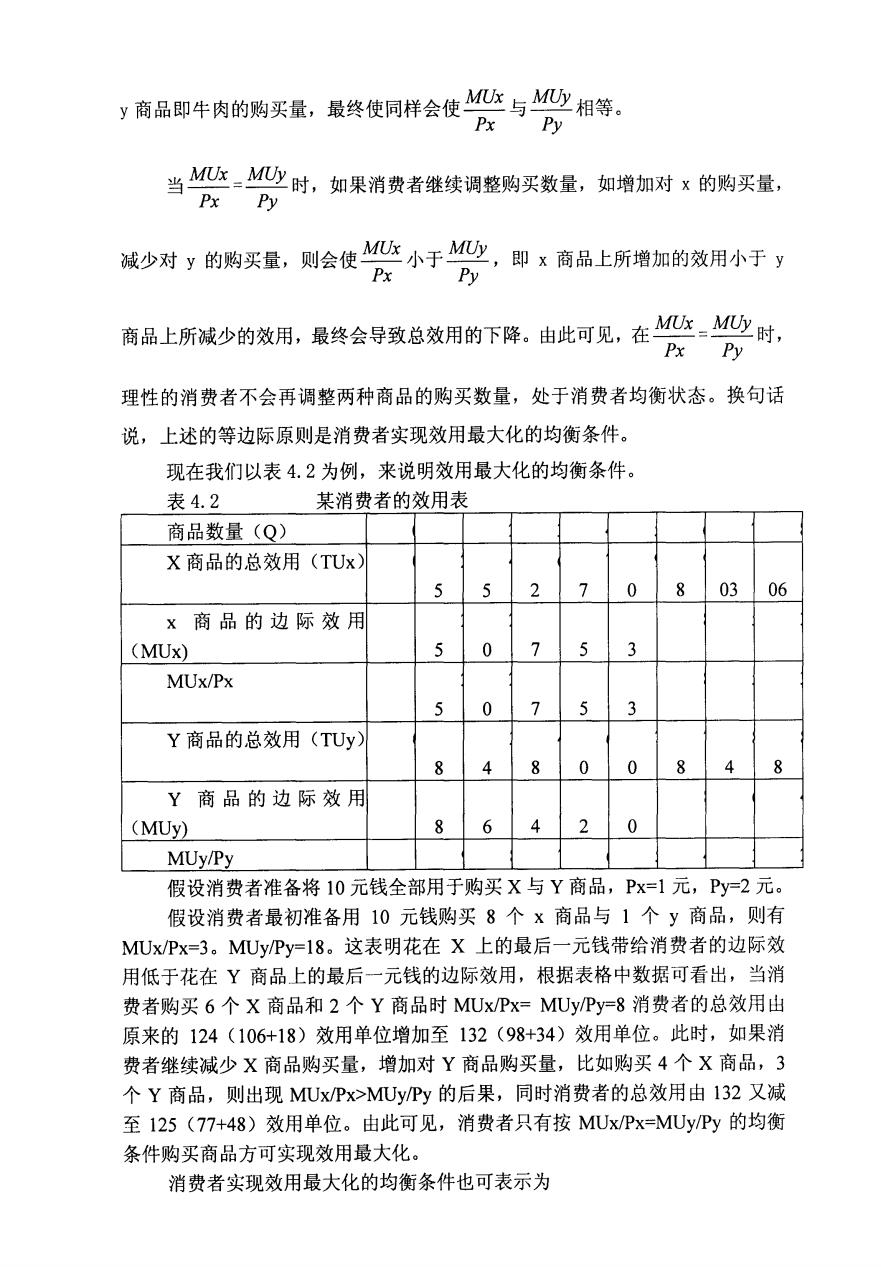
y商品即牛肉的购买量,最终使同样会使Mx与M心相等。 Px Py 当M:M心时,如果消费者继续调整购买数量,如增加对x的购买量, Px Py 减少对y的购买量,则会使M:小于M心,即x商品上所增加的效用小于y Px Py 商品上所减少的效用,最终会导致总效用的下降。由此可见,在x=M少时, Px Py 理性的消费者不会再调整两种商品的购买数量,处于消费者均衡状态。换句话 说,上述的等边际原则是消费者实现效用最大化的均衡条件。 现在我们以表4.2为例,来说明效用最大化的均衡条件。 表4.2 某消费者的效用表 商品数量(Q) X商品的总效用(TUx) 5 5 2 7 0 803 06 ×商品的边际效用 (MUx) 5 0 3 MUx/Px 5 0 个 5 3 Y商品的总效用(TUy) 8 4 8 0 0 8 4 8 Y商品的边际效用 (MUy) 8 6 4 2 0 MUy/Py 假设消费者准备将10元钱全部用于购买X与Y商品,Px=1元,Py=2元。 假设消费者最初准备用10元钱购买8个×商品与1个y商品,则有 MUx/Px=3。MUy/Py-=l8。这表明花在X上的最后一元钱带给消费者的边际效 用低于花在Y商品上的最后一元钱的边际效用,根据表格中数据可看出,当消 费者购买6个X商品和2个Y商品时MUx/Px-=MUy/Py=8消费者的总效用由 原来的124(106+18)效用单位增加至132(98+34)效用单位。此时,如果消 费者继续减少X商品购买量,增加对Y商品购买量,比如购买4个X商品,3 个Y商品,则出现MUx/Px>MUy/Py的后果,同时消费者的总效用由132又减 至125(77+48)效用单位。由此可见,消费者只有按MUx/Px=MUy/Py的均衡 条件购买商品方可实现效用最大化。 消费者实现效用最大化的均衡条件也可表示为

MUx Px (4.8) MUy Py 该公式的左侧反映了消费者对两种商品的主观评价,右侧反映了市场对两 种商品的客观评价。当消费者的主观评价与市场的客观评价相一致时,消费者 方可实现效用最大化。 值得注意的是,上述的消费者均衡条件暗含一个假设:商品的单位可以被 细分为任意小的部分。对于白糖和食盐之类的商品,基于符合这个假设,消费 者可以通过对其购买量做细小的调整,使花在这两种商品上的最后一单位货币 所实现的边效用相等。但是对于诸如汽车之类商品,其购买单位为辆,从而无 法像白糖一样被任意细分为很小的部分。此时,一个家庭购买一辆汽车时,花 在汽车上的最后一单位货币的边际效用也许大于花在其他物品的最后一单位货 币的边际效用,按照上述的均衡条件,消费者应该增加对汽车的购买。但是, 如果消费者购买了第二辆汽车,又可能由于汽车的边际效用大减,使得花在汽 车上的最后一单位货币的边际效用小于花在其他物品上的最后一单位货币的边 际效用。因此,现实中许多物品的购买单位无法任意细分的事实,使得消费者 花在各种物品上的最后一单位货币的边际效用不是完全相等,而是比较接近。 此外,可能会有人指出,消费者在市场上购物时,并没有去按照效用最大 化原则进行快速计算,然后确定其购买方案,因此效用最大化条件没有任何实 际意义。经济学家何不赞同这个说法。经济学家们认为,其一,在许多情况下 消费才在购物时,并非常且随决购买,而是进行了某些考虑:其二,虽然消费 者不一定知晓效用最大化条件,但是效用最大化条件却可以对消费者的行为进 行最大化条件,但是效用最大化条件却可以对消费者行为进行解释和预测。著 名的经济学家米尔顿·弗里德曼曾在这方面有着精彩的论述。他指出,专业台 球手大都不懂经典物理学,但是如果台球手遵守经典物理学中的速度、力量以 及角度方面的定律,他们就会成功地击到球。因此,物理定律可以精确地解释 和预测台球手的行为,庆当作为职业先手如何击球的恰当的理论模型,弗里德 曼这一论述反映了包括效用最大化条件在内的甩的经济模型的作用。 效用最大化条件还可应用于生活中许多领域。比如消费者在分配时间时, 应使自己花费在每一种活动上的最后一分钟的边际效用都盯等,才算是最佳利 用了时间。 五、需求定理的解释 根据上述的消费均衡条件,我们可以解释为什么,商品价格与需求之间通 常存在着反向变动关系。 假设消费者选择几种商品,且最初处于均衡状态,即MUP,=MU,P2= =MU,P=λ。在其他条件不变的情况下,如果第一种商品价格上升,会使得 MU,P,数值下降,即花在第一种商品上的最后一单位货币带来的边际效用低于 花在其他商品上的最后一单位货币边际效用。理性的消费者将会减少对第一种 商品的购买量使得第一种商品的边际效用上升,从而使MU,P,的数值再度等于

其综商品的边际效用与价格之比。由此可见在一种商品价格上升时,消费者为 了实现效用最大化,会减少对该商品的需求量。同理可以说明。一种商品价格 下降时,消费者对该商品的需求量将会增加。 下面我们以具体的数字为例来解释需求法则。假设消费者所购买的X商品 的边际效用数值如表4.1所示,一元货币的边际效用为】效用单位,消费者效 用最大化原则MU/P=λ来购买商品。 当X商品的单位价格为5元时,根据上述均衡原则可知,商品的边际效用 应为5效用单位(MU=P·入=5元·/效用单位/元=5效用单位)。由表4.1可知, 消费者应该购买一单位X商品。同理可知当Px=4元时,为了实现效用最大化, X商品的边际效用应为4效用单位,消费者应为4效用单位,消费者应该购买 两个单位的X商品;Px=3时,消费者应该购买单位的X商品,等等。 上述例子中的价格与需求量之间的反向变动关系也可以用几何图形来表 示,如图4.2所示。 图4.2需求曲线的形成 六、消费者剩余(Consumer's Surplus) 消费者剩余是指消费者在购买一定量的某种商品时,他所愿意支付的货币 额超过实际支付的货币额的差额。 消费者在购买商品时,他所愿意支付的货币额的大小,取决于他对该商品 的总效用的评价,而他所实际支付的货币额的大小,则取决于该商品的市场价 格。比如,某消费者准备购买一辆自行车,自行车的市场价格为300元,而在 消费者看来,一辆自行车能给自己带来450效用单位的效用,或者说一辆自行 车值450元(假设一元货币的效用为一个效用单位),自己为一辆自行车所愿支 付的价格即为450元。由此可见,如果该消费者购买一辆自行车,将会得到150 元(450元一300元)的消费者剩余: 那么,为什么消费者在购买商品时,可能会得到消费者剩余呢?这是因为, 消费者在按照既定的市场价格购买商品时,从第一单位商品到最后一单位商品, 他所实际支付的价格都是相同的。但是,这个既定的实际支付的价格仅仅与他 对最后一单位商品所愿意支付的货币额相等(MU/入=P)。根据边际效用递减规 律,前面各单位商品具有更高的边原效用,消费者对之愿意支付更高的货币额。 由此消费者从前面每一单位商品的消费中享受了消费者剩余。 有关消费者剩余的计算方法,可以结合表4.1和图4.2中的数字来说明如 表4.3所示。 表4.3 某商品的消费者剩余 市 需求 愿意支付的货币 实际支付的货币 消费者剩 场价格 量(个) 额(元) 额(元) 余(元) 5 5 J 0 4 2 9 8 1 3 3 12 9