
都会使人们减少对毒品的使用。但是,哪一种手段可以更有效地稳定社会秩序, 还要结合弹性理论来分析。 从短期来看,由于许多人已经吸毒上瘾,因此,高价格并不能使其对对毒 品使用量有明显减少,换句话说,这些人对毒品的需求是缺乏弹性的。因此, 增加对贩毒者打击力度,使得毒品价格上升后,吸毒者为使用毒品所需支出的 货币额增大。为了能够有足够的钱去吸毒,他们会更加频繁地进行犯罪活动, 使社会秩序更加不稳定。反之,增加对吸毒者的说服教育,使毒品价格下降, 会使吸毒者使用毒品所需支出的货币额降低,从而可能使其减少相关的犯罪活 动。 从长期来看,会有一些青少年加入吸毒者的队伍中,由于接触毒品时间较 短,许多人尚未吸毒成瘾,同时吸毒的支出在其预算中占有非常大的比重,因 此,青少年对毒品的需求价格弹性可能是大于1的。在这种情况下,增大对贩 毒者的打击力度,提高了毒品价格,会使相当大数量的青少年停止使用毒品。 从更长远的观点看,毒品长期保持高价,会使一个国家吸毒者的人数绝对地下 降(因为年纪大的成瘾吸毒者最终会死去,而新的潜在的吸毒者被高价挡在毒 品大门外)。与之相反,在长期内,如果采用说服教育手段,使毒品价格一直较 低,则可能使青少年这些潜在的吸毒者很容易地进入毒品市场,不利于对毒品 的最终控制。 第三章附录I—需求点弹性系的几何计算公式的推导 我们将图3-2移植过来,计算A点的点弹性系数。根据公式,有 m=do p dP o 其中吧为需求曲线在A点的斜率的倒数,根据图形可知: dp OC AO dp do OB B 因此=9B dP AO 由此可计算出: n-08.P-28.10g8 an A2 A0 00 A0 AC 故需求曲线上任一点的需求弹性的数值,等于该点以下的切线段的长度与该点 以上的切线线段的长度之比。 第三章附录II—需求弹性系数与总收益之间关系的数学证明

证明:对于反需求函数P=f(Q)。 可以计算出TR=P·Q=Q·f(Q)。 企业价格变动对总收益的影响为 因为Q>0,由此可以得到以下三种情况: (1)当<1时,>0,即价格上升,总收益增加:价格下降,总收益减 dp 少。 (2)当4>1时,<0,即价格上升总收益减少:价格下降,总收益增加。 ap (3)当na=1时, 迟=0,即无论价格如何变动,总收益保持不变。 dp 第三章附录III—一恩格尔法则的数学证明 假设某种商品的价格始终为P。消费者的收放及其对该商品的需求量最初为 I和Q。此后,消费者的收入增加了△单位,由此导致他对该商品的需求增加 了△Q单位。 根据上述条件,可知: 收入变动前商品支出在收入中所占的百分比(即恩格尔系数)E,=P: 收入变动后商品支出在收入中所占百分比 E,=P:+4g I+△ 其中,为商品的需求收入弹性系数。显然,当该商品的需求收入弹性小于 1时(如食品),E,<E,即随着消费者收入增加,该商品支出在收入中所占比重 降1△1第三章附录V一供给弹性的几何计算方法 当供给曲线为一条向右上方倾斜的直线时,我们可以运用几何方法判断它的点 弹性系数的大小。 图3-15供给曲线与点弹性系数的计算 在图3-15中,商品的供给曲线的延长线交横轴于A点。供给曲线上任一点 G所对应的价格与数量分别为0P,和OQ。 根据弹性系数计算公式,G点的供给弹性为

(其中GQ<OP) 由此可见,当供给曲线的延长线先与横轴相交时,该供给曲线上任一点的 点弹性系数一定小于1。 关于供给点弹性系数大于1和等于1的两种情况,同学样可采用类似方法 自行证明

第三章确定条件下消费者的选择 在第二章中,我们结合供求曲线的基本特征论述了均衡价格的决定等问 题。自本章开始,我们将对决定供求曲线特征的内在因素作进一步的分析。其 中,在第四章,我们将分析在确定条件下(即无风险条件下)的消费者行为, 进而解释为什么需求曲线会向右下方倾斜。第五章将分析不确定条件下消费的 选择,以进一步丰富消费者行为理论。第六、七、八章则对企业的生产、成本 和市场理论进行分析,进而说明为什么供给曲线会向右上方倾斜。 在本章中,我们分别采用基数效用和序数效用两种分析方法对消费者行为 进行分析。 第一节 基数效用与消费者均衡 一、效用(Utility) 效用的定义可以从消费的主体与客体两个方面进行表述。从消费的主体来 讲,效用是指人们在消费某种商品时所得到的满足程度:从消费的客体来讲, 效用是指商品满足人们的欲望的能力。由此可见,对于消费者来说,一种商品 是否具有效用,既要取决于消费者对该商品是否具有欲望,又要取决于该商品 是否具有满足该消费者欲望的能力。比如,人们具有吃穿方面的欲望,而粮食 和衣服恰好能够满足这一方面的欲望,因此粮食和衣服具有效用。 与效用概念相对立的另一个概念是负效用(Disutility)。负效用是指某种 物品所具有的导致人们不舒服或痛苦的能力。比如环境污染等。 二、基数效用(Cardinal Utility) 十九世纪和二十世纪初的一些经济学家们认为,效用作为心理上的一种实 际存在,是可以像长度和温度一样加以衡量的。他们的观点被称为基数效用理 论。 基数这个术语来自于数学。基数是指数字1、2、3等。基数效用理论认为, 物品效用的大小可以用基金1、2、3等表示;效用可以加总求和:计量效用大 小的单位被称为效用单位。比如,某个消费者可以准确地告诉我们,一辆小轿 车带给他的效用是40效用单位,一部手机带给他们的效用是20效用单位,小 轿车的效用是手机效用的2倍,小轿车与手机的效用之和是60效用单位。 三、总效用(Total Utility TV)与边际效用(Marginal Utility,MU) 总效用是指消费才在一定时间内从一定量的某种商品的消费中所获得的总 满足程度。假定消费者对某一种商品的消费量为Q,则总效用函数可表示为: TU=f(O) 边际效用是指消费者在一定时间内每增加一单位某种商品的消费所增加的 满足程度。边际效用函数可以表示为: MU= △TU(Q) (4.2) △Q
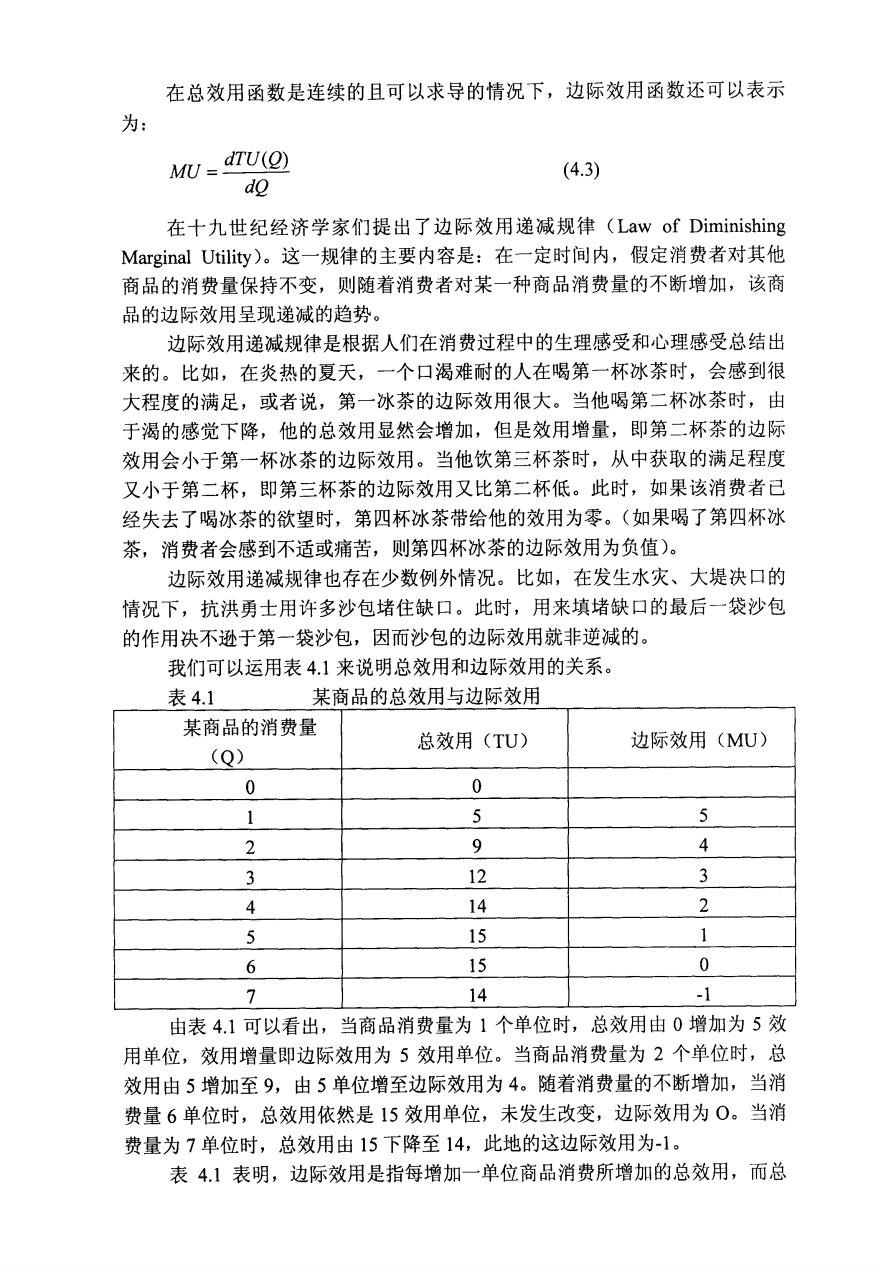
在总效用函数是连续的且可以求导的情况下,边际效用函数还可以表示 为: MU dTu(Q) (4.3) do 在十九世纪经济学家们提出了边际效用递减规律(Law of Diminishing Marginal Utility)。这一规律的主要内容是:在一定时间内,假定消费者对其他 商品的消费量保持不变,则随着消费者对某一种商品消费量的不断增加,该商 品的边际效用呈现递减的趋势。 边际效用递减规律是根据人们在消费过程中的生理感受和心理感受总结出 来的。比如,在炎热的夏天,一个口渴难耐的人在喝第一杯冰茶时,会感到很 大程度的满足,或者说,第一冰茶的边际效用很大。当他喝第二杯冰茶时,由 于渴的感觉下降,他的总效用显然会增加,但是效用增量,即第二杯茶的边际 效用会小于第一杯冰茶的边际效用。当他饮第三杯茶时,从中获取的满足程度 又小于第二杯,即第三杯茶的边际效用又比第二杯低。此时,如果该消费者已 经失去了喝冰茶的欲望时,第四杯冰茶带给他的效用为零。(如果喝了第四杯冰 茶,消费者会感到不适或痛苦,则第四杯冰茶的边际效用为负值)。 边际效用递减规律也存在少数例外情况。比如,在发生水灾、大堤决口的 情况下,抗洪勇士用许多沙包堵住缺口。此时,用来填堵缺口的最后一袋沙包 的作用决不逊于第一袋沙包,因而沙包的边际效用就非逆减的。 我们可以运用表41来说明总效用和边际效用的关系。 表4.1 某商品的总效用与边际效用 某商品的消费量 总效用(TU) 边际效用(MU) (Q) 0 0 1 5 5 2 9 ¥ 3 12 3 4 14 w 5 15 6 15 0 7 14 -1 由表4.1可以看出,当商品消费量为1个单位时,总效用由0增加为5效 用单位,效用增量即边际效用为5效用单位。当商品消费量为2个单位时,总 效用由5增加至9,由5单位增至边际效用为4。随着消费量的不断增加,当消 费量6单位时,总效用依然是15效用单位,未发生改变,边际效用为0。当消 费量为7单位时,总效用由15下降至14,此地的这边际效用为-1。 表4.1表明,边际效用是指每增加一单位商品消费所增加的总效用,而总