
d 按照公式(2416)计算标准差的无偏估计:S=2一=2.70 技盟公式241)计算变异系:C-10%=04134: 2.4.3分布的偏度和峰度 (一)偏度系数测度地理数据分布的不对称性情况,刻画以平均值为中心的偏向情况, 计算公式为: 8=5) (2.4.19) g1<0,表示负偏,即均值在峰值的左边:g1>0,表示正偏,即均值在蜂值的右边: 1=0,表示对称分布(如下图)。 图2.4.1偏度系数的三种情形 例8对于表2.44中的数据分布,计算其标准偏度系数。 解题步骤及分析: 按照公式(2.4.19),计算可得g1=-0.308756<0。显然,结果为负偏,即平均值在峰值的 边。 (二)标准蜂度系数。它测度了地理数据在均值附近的集中程度,其计算公式为 &。-3 (2.4.20) 标准正态分布的标准峰度系数2=0:g20,表示地理数据分布的集中程度高于正态分 布:2<0,表示地理数据分布的集中程度低于正态分布(见上图)。 例9对于表2.4.24的数据分布,计算其标准峰度系数。 按照公式(2420),代入数据计算可得=0.868<0。显然,其分布的集中程度低 于正态分布。 24.4应用实例中国大陆省份人均GDP的变异系数 是影数名代表中国名省市、自治区)的人均G0P测由公试2413》计算得到的变一 Cv就测度了中国经济发展水平的省际差异.利用各省(市、自治区)的人均GDP 分别计算了1978~1999各年的变异系数(如下图)
按照公式(2.4.16)计算标准差的无偏估计: 22.70 12 1 2 = − = d S ; 按照公式(2.4.17)计算变异系: = ×100% = 0.4184 x S Cv ; 2.4.3 分布的偏度和峰度 (一)偏度系数 测度地理数据分布的不对称性情况,刻画以平均值为中心的偏向情况, 计算公式为: (2.4.19) g1<0,表示负偏,即均值在峰值的左边;g1>0,表示正偏,即均值在峰值的右边; g1 =0,表示对称分布(如下图)。 例 8 对于表 2.4.4 中的数据分布,计算其标准偏度系数。 解题步骤及分析: 按照公式(2.4.19),计算可得 g1= -0.308756<0。显然,结果为负偏,即平均值在峰值的 边。 (二)标准峰度系数。它测度了地理数据在均值附近的集中程度,其计算公式为 (2.4.20) 标准正态分布的标准峰度系数 g2 =0;g2>0,表示地理数据分布的集中程度高于正态分 布;g2<0,表示地理数据分布的集中程度低于正态分布(见上图)。 例 9 对于表 2.4.24 的数据分布,计算其标准峰度系数。 按照公式(2.4.20),代入数据计算可得 g2 =-0.868<0。显然,其分布的集中程度低 于正态分布。 2.4.4 应用实例 中国大陆省份人均 GDP 的变异系数 以 xi 代表中国各省(市、自治区)的人均 GDP,则由公式(2.4.13)计算得到的变 异系数 Cv 就测度了中国经济发展水平的省际差异。利用各省(市、自治区)的人均 GDP, 分别计算了 1978~1999 各年的变异系数(如下图)。 图2.4.1 偏度系数的三种情形 3 1 1 1 ∑= ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = n i i x x n g σ ( ) 3 1 4 1 2 − − = ∑= σ x x n g i n i
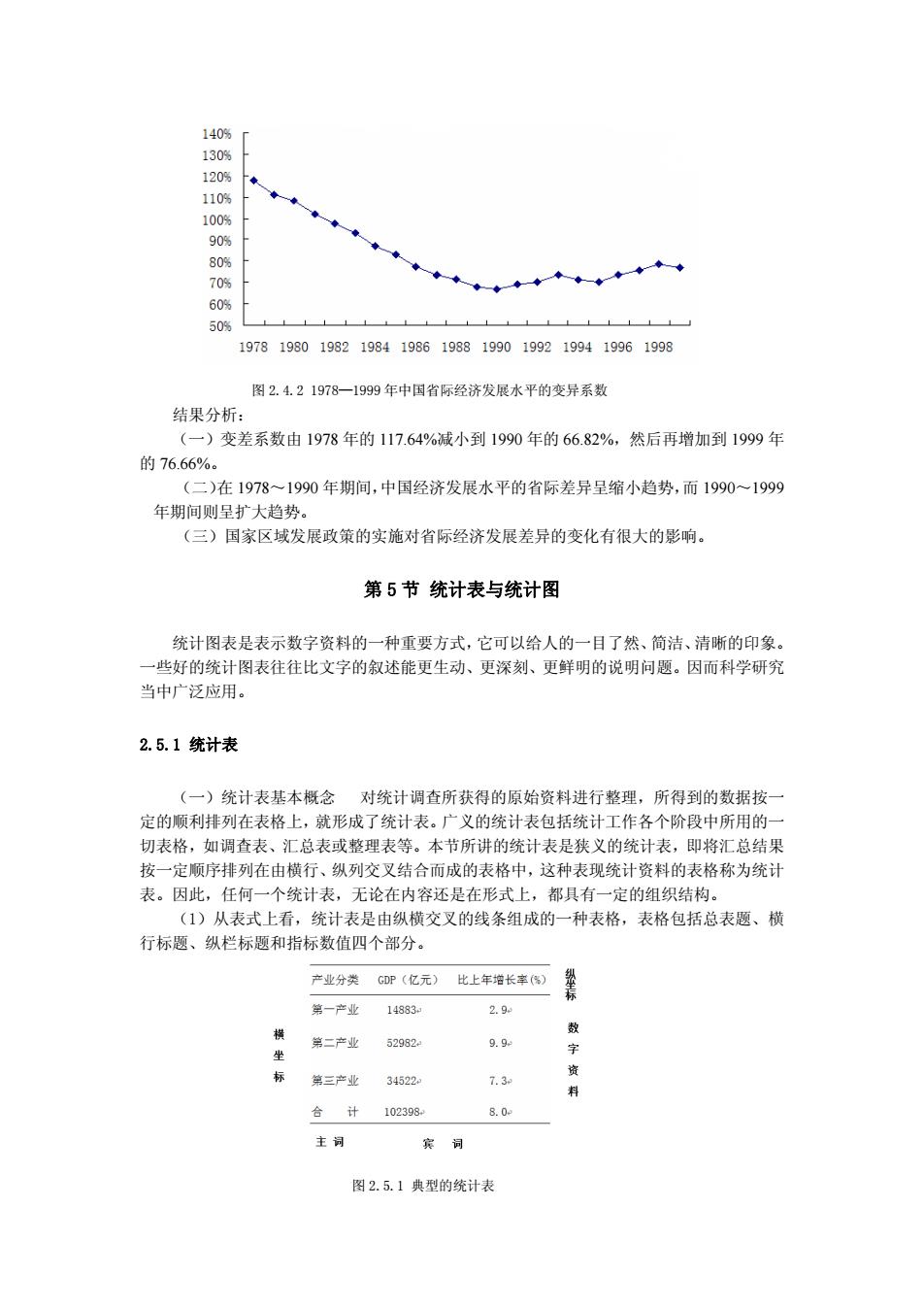
140% 130% 120% 60 19781980198219841986198819901992199419961998 图2.4.21978一1999年中国省际经济发展水平的变异系数 结果分析: (一)变差系数由1978年的117.64%减小到1990年的66.82%,然后再增加到1999年 的76.66%。 (二)在1978一1990年期间,中国经济发展水平的省际差异呈缩小趋势,而1990一1999 年期间则呈扩大趋势。 (三)国家区域发展改策的实施对省际经济发展差异的变化有很大的影响。 第5节统计表与统计图 统计图表是表示数字资料的一种重要方式,它可以给人的一目了然、简洁、清晰的印象。 一些好的统计图表往往比文字的叙述能更生动、更深刻、更鲜明的说明问题。因而科学研究 当中广泛应用。 2.5.1统计表 (一)统计表基本概念对统计调查所获得的原始资料进行整理,所得到的数据按 定的顺利排列在表格上,就形成了统计表。广义的统计表包括统计工作各个阶段中所用的 切表格,如调查表、汇总表或整理表等。本节所讲的统计表是狭义的统计表,即将汇总结果 按一定顺序排列在由横行、纵列交叉结合而成的表格中,这种表现统计资料的表格称为统计 表。因此,任何一个统计表,无论在内容还是在形式上,都具有一定的组织结构, (1)从表式上看,统计表是由纵横交叉的线条组成的一种表格,表格包括总表题、横 行标题、纵栏标题和指标数值四个部分。 产业分类GP(亿元)比上年增长幸))量 第-产业14883 2.9 第二产业52962 9.9e 坐 标 第三产业34522 7.3 合计102398 主词 宾河 图2.5.1典型的统计表
图 2.4.2 1978—1999 年中国省际经济发展水平的变异系数 结果分析: (一)变差系数由 1978 年的 117.64%减小到 1990 年的 66.82%,然后再增加到 1999 年 的 76.66%。 (二)在 1978~1990 年期间,中国经济发展水平的省际差异呈缩小趋势,而 1990~1999 年期间则呈扩大趋势。 (三)国家区域发展政策的实施对省际经济发展差异的变化有很大的影响。 第 5 节 统计表与统计图 统计图表是表示数字资料的一种重要方式,它可以给人的一目了然、简洁、清晰的印象。 一些好的统计图表往往比文字的叙述能更生动、更深刻、更鲜明的说明问题。因而科学研究 当中广泛应用。 2.5.1 统计表 (一)统计表基本概念 对统计调查所获得的原始资料进行整理,所得到的数据按一 定的顺利排列在表格上,就形成了统计表。广义的统计表包括统计工作各个阶段中所用的一 切表格,如调查表、汇总表或整理表等。本节所讲的统计表是狭义的统计表,即将汇总结果 按一定顺序排列在由横行、纵列交叉结合而成的表格中,这种表现统计资料的表格称为统计 表。因此,任何一个统计表,无论在内容还是在形式上,都具有一定的组织结构。 (1)从表式上看,统计表是由纵横交叉的线条组成的一种表格,表格包括总表题、横 行标题、纵栏标题和指标数值四个部分。 图 2.5.1 典型的统计表

总表题是统计表的名称,它扼要地说明该表的基本内容。它置于统计表格的正上方。横 行标题是横行的名称,一般放在表格的左方。纵栏标题是纵栏的名称,一般放在表格的上方】 指标数值列在横行和纵栏的交叉处,用来说明总体及其组成部分的数量特征,它是统计表格 的核心部分。 (2)从内容上看,统计表由主词栏和宾词栏两个部分组成。主词栏是统计表所要说明 的总体及其组成部分:宾词栏是统计表用来说明总体数量特征的各个统计指标。图2.4.1 早现了统计表内容和形式结构上的所有信息。 (二)统计表的分类统计表按结构的组织方式可以分成不同的类型。 (1)按主词的结构分类根据主词是否分组和分组的程度,分为简单表、分组表和复 合表。主词未经任何分组的统计表称为简单表,也称一览表。主词罗列各单位的名称:分组 表是主词只按一个标志进行分组形成的统计表,也称简单分组表:主词按两个或两个以上标 志进行分组的统计表称为复合表,也称复合分组表。 (2)按宾词设计分类按宾词设计统计表可分为宾词简单排列、分组平行排列和分组 层叠排列等。宾词简单排列: 词 进行任何分组,按一定顺序排列在统计表上:宾词分 平行排列:宾词栏中各分组标志彼此分开,平行排列:宾词分组层叠排列:统计指标同时有 层次地按两个或两个以上标志分组,各种分组层叠在一起,宾词的栏数等于各种分组的组数 连乘积。 (三)统计表的设计统计表设计,遵循一定的要求。这些要求,虽然按照具体的内容 有所不同,总体上可以概括简练 明确 实用 美观、便于比较等几个基本点 (1)线条的绘制表的上下端应以粗线绘制,表内纵横线以细线绘制。两端一般不划 线,采用“开口式” (2)合计栏的设统计表各纵列若需合计时,一般应将合计列在最后一行,各横行若 需要合计时,可将合计列在最前一栏或最后一栏。 (3)标题设计统计表的总标题,横栏、纵栏标题应简明扼要,以简练而又准确的文 字表述统计资料的内容、资料所属的空间和时间范围, (4)指标数值表中数字应该填写整齐,对准位数。当数字小且可略而不计时,可写 上“0”:当缺某项数字资料时,可用符号“”:不应有数字时用符号“一”表示。 (5)计最单位统计表必须注明数字资料的计量单位。当全表只有一种计量单位时, 可以把它写在表头的上方。如果表中各格的指标数值计量单位不同,可在横行标题后添一列 十量单位 (6)注解或资料来源必要时,在统计表下应加注解或说明,以便查考。 (四)统计分组统计表的制作与数据统计整理过程中经常遇到统计分组问题。 表2.5】某县人工造林地面积饿统计分组数据 分组序号12 345 6 7 8 9 10 分组标志0,】1,2】(2,3】3,4(4,5](6,616,7刀(,8】(8,9)9,10]10,1) 组中值0.51.5253.545556.57.58.5 9.5 10.5 频数2596136214253286260203154 85 24 频率1.45.537.8312.3145716.4714.9811.698.87 4.90 1.38 向上累计 5 1212574717241010127014731627 1712 1736 频数 向下累计 。频致 173617111615147912651012726466263109 24
总表题是统计表的名称,它扼要地说明该表的基本内容。它置于统计表格的正上方。横 行标题是横行的名称,一般放在表格的左方。纵栏标题是纵栏的名称,一般放在表格的上方。 指标数值列在横行和纵栏的交叉处,用来说明总体及其组成部分的数量特征,它是统计表格 的核心部分。 (2)从内容上看,统计表由主词栏和宾词栏两个部分组成。主词栏是统计表所要说明 的总体及其组成部分;宾词栏是统计表用来说明总体数量特征的各个统计指标。图 2.4.1 呈现了统计表内容和形式结构上的所有信息。 (二)统计表的分类 统计表按结构的组织方式可以分成不同的类型。 (1)按主词的结构分类 根据主词是否分组和分组的程度,分为简单表、分组表和复 合表。主词未经任何分组的统计表称为简单表,也称一览表。主词罗列各单位的名称;分组 表是主词只按一个标志进行分组形成的统计表,也称简单分组表;主词按两个或两个以上标 志进行分组的统计表称为复合表,也称复合分组表。 (2)按宾词设计分类 按宾词设计统计表可分为宾词简单排列、分组平行排列和分组 层叠排列等。宾词简单排列:宾词不进行任何分组,按一定顺序排列在统计表上;宾词分组 平行排列:宾词栏中各分组标志彼此分开,平行排列;宾词分组层叠排列:统计指标同时有 层次地按两个或两个以上标志分组,各种分组层叠在一起,宾词的栏数等于各种分组的组数 连乘积。 (三)统计表的设计 统计表设计,遵循一定的要求。这些要求,虽然按照具体的内容 有所不同,总体上可以概括简练、明确、实用、美观、便于比较等几个基本点。 (1)线条的绘制 表的上下端应以粗线绘制,表内纵横线以细线绘制。两端一般不划 线,采用“开口式”。 (2)合计栏的设 统计表各纵列若需合计时,一般应将合计列在最后一行,各横行若 需要合计时,可将合计列在最前一栏或最后一栏。 (3)标题设计 统计表的总标题,横栏、纵栏标题应简明扼要,以简练而又准确的文 字表述统计资料的内容、资料所属的空间和时间范围。 (4)指标数值 表中数字应该填写整齐,对准位数。当数字小且可略而不计时,可写 上“0”;当缺某项数字资料时,可用符号“” ;不应有数字时用符号“-”表示。 (5)计量单位 统计表必须注明数字资料的计量单位。当全表只有一种计量单位时, 可以把它写在表头的上方。如果表中各格的指标数值计量单位不同,可在横行标题后添一列 计量单位。 (6)注解或资料来源 必要时,在统计表下应加注解或说明,以便查考。 (四)统计分组 统计表的制作与数据统计整理过程中经常遇到统计分组问题。 表 2.5.1 某县人工造林地面积饿统计分组数据 分组序号 1 2 3 4 5 6 7 8 9 10 11 分组标志 (0,1] (1,2] (2,3] (3,4] (4,5] (5,6] (6,7] (7,8] (8,9] (9,10] (10,11) 组中值 0.5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10. 5 频数 25 96 136 214 253 286 260 203 154 85 24 频率 1.44 5.53 7.83 12.33 14.57 16.47 14.98 11.69 8.87 4.90 1.38 向上累计 频数 25 121 257 471 724 1010 1270 1473 1627 1712 1736 向下累计 频数 1736 1711 1615 1479 1265 1012 726 466 263 109 24
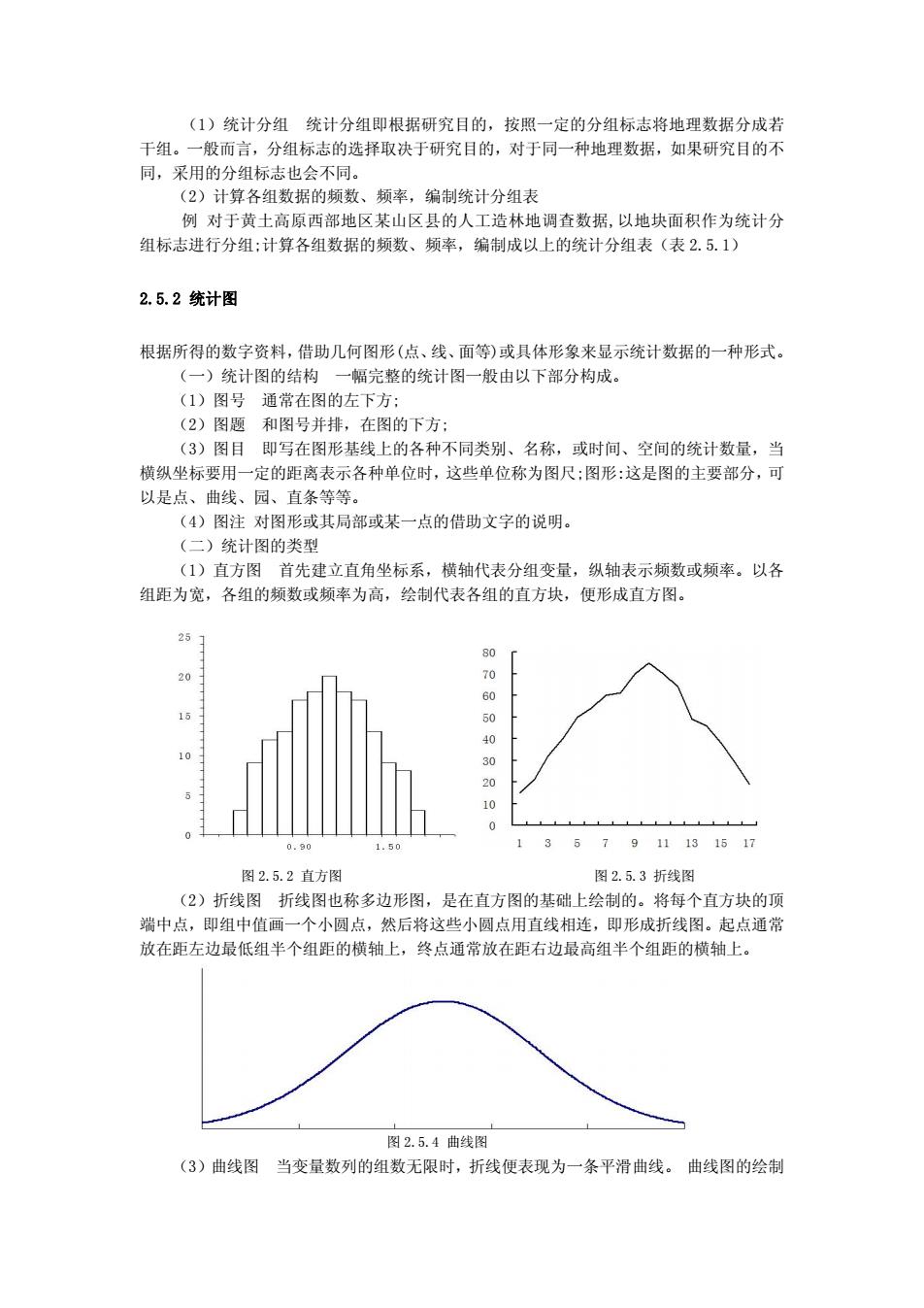
(1)统计分组统计分组即根据研究目的,按照一定的分组标志将地理数据分成若 干组。一般而言,分组标志的选择取决于研究目的,对于同一种地理数据,如果研究目的不 同,采用的分组标志也会不同 (2) 计算各组数据的频数、频率,编制统计分组表 例对于黄土高原西部地区某山区县的人工造林地调查数据,以地块面积作为统计分 组标志进行分组:计算各组数据的频数、频率,编制成以上的统计分组表(表2.5.1) 2.5.2统计图 根据所得的数字资料,借助几何图形(点、线、面等)或具体形象来显示统计数据的一种形式。 (一)统计图的结构 一幅完整的统计图一般由以下部分构成。 (1)图号通常在图的左下方: (2)图题和图号并排,在图的下方: (3)图目即写在图形基线上的各种不同类别、名称,或时间、空间的统计数最,当 横纵坐标要用一定的 离表示各种单位时,这些单位称为图尺:图形:这是图的主要部分,可 以是点、曲线、园、直条等等。 (4)图注对图形或其局部或某一点的借助文字的说明。 (二)统计图的类型 (1)直方图首先建立直角坐标系,横轴代表分组变量,纵轴表示频数或频率。以各 组距为宽,各组的频数或频率为高,绘制代表各组的直方块,便形成直方图。 0.90 135791113151 图2.5.2直方图 图2.5.3折线图 (2)折线图折线图也称多边形图,是在直方图的基础上绘制的。将每个直方块的顶 端中点,即组中值画一个小圆点,然后将这些小圆点用直线相连,即形成折线图。起点通常 放在距左边最低组半个组距的横轴上,终点通常放在距右边最高组半个组距的横轴上。 图2.5.4曲线图 (3)曲线图当变量数列的组数无限时,折线便表现为一条平滑曲线。曲线图的绘制
(1)统计分组 统计分组即根据研究目的,按照一定的分组标志将地理数据分成若 干组。一般而言,分组标志的选择取决于研究目的,对于同一种地理数据,如果研究目的不 同,采用的分组标志也会不同。 (2)计算各组数据的频数、频率,编制统计分组表 例 对于黄土高原西部地区某山区县的人工造林地调查数据,以地块面积作为统计分 组标志进行分组;计算各组数据的频数、频率,编制成以上的统计分组表(表 2.5.1) 2.5.2 统计图 根据所得的数字资料,借助几何图形(点、线、面等)或具体形象来显示统计数据的一种形式。 (一)统计图的结构 一幅完整的统计图一般由以下部分构成。 (1)图号 通常在图的左下方; (2)图题 和图号并排,在图的下方; (3)图目 即写在图形基线上的各种不同类别、名称,或时间、空间的统计数量,当 横纵坐标要用一定的距离表示各种单位时,这些单位称为图尺;图形:这是图的主要部分,可 以是点、曲线、园、直条等等。 (4)图注 对图形或其局部或某一点的借助文字的说明。 (二)统计图的类型 (1)直方图 首先建立直角坐标系,横轴代表分组变量,纵轴表示频数或频率。以各 组距为宽,各组的频数或频率为高,绘制代表各组的直方块,便形成直方图。 图 2.5.2 直方图 图 2.5.3 折线图 (2)折线图 折线图也称多边形图,是在直方图的基础上绘制的。将每个直方块的顶 端中点,即组中值画一个小圆点,然后将这些小圆点用直线相连,即形成折线图。起点通常 放在距左边最低组半个组距的横轴上,终点通常放在距右边最高组半个组距的横轴上。 图 2.5.4 曲线图 (3)曲线图 当变量数列的组数无限时,折线便表现为一条平滑曲线。 曲线图的绘制
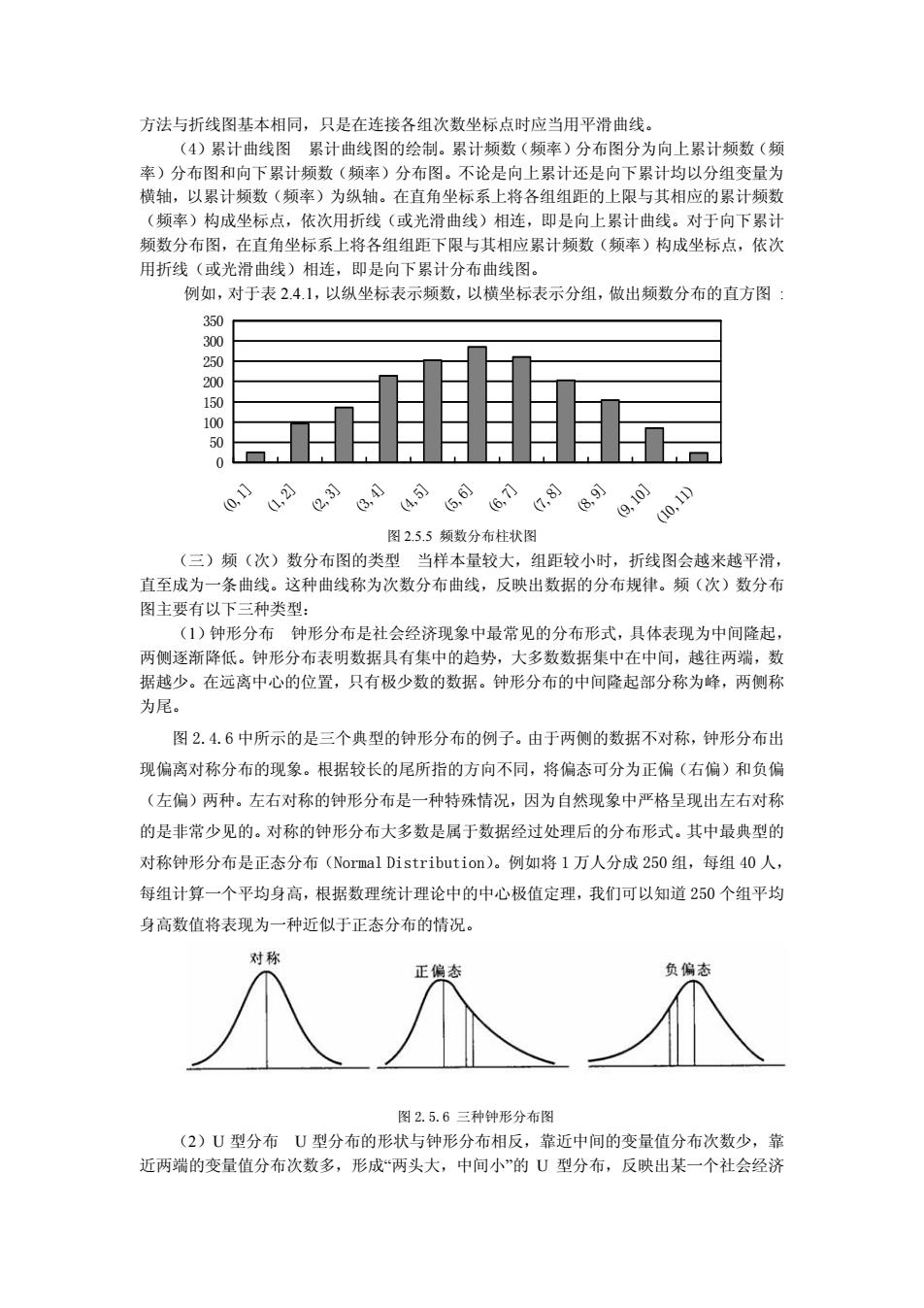
方法与折线图基本相同,只是在连接各组次数坐标点时应当用平滑曲线。 (4)累计曲线图累计曲线图的绘制。累计频数(频率)分布图分为向上累计频数(频 率)分布图和向 下累计频数(频率)分布图。不论是向上累计还是向下累计均以分组变量为 横轴,以累计频数(频率)为纵轴。在直角坐标系上将各组组距的上限与其相应的累计频 (频率)构成坐标点,依次用折线(或光滑曲线)相连,即是向上累计曲线。对于向下累计 频数分布图,在直角坐标系上将各组组距下限与其相应累计颍数(频率)构成坐标点,依次 用折线(或光滑曲线)相连,即是向下累计分布曲线图。 例如,对于表2.4.1,以纵坐标表示频数,以横坐标表示分组,做出频数分布的直方图 0o0 .0 0.1 图25.5频数分布柱状图 (三)频(次)数分布图的类型当样本量较大,组距较小时, 折线图会越来越平滑 直至成为一条曲线。这种曲线称为次数分布曲线,反映出数据的分布规律。频(次)数分在 图主要有以下三种类型: (1)钟形分布钟形分布是社会经济现象中最常见的分布形式,具体表现为中间隆起, 两侧逐渐降低。钟形分布表明数据具有集中的趋势,大多数数据集中在中间,越往两端,数 据越少。在远离中心的位置,只有极少数的数据。钟形分布的中间降起部分称为峰, 两侧称 为尾。 图2.4.6中所示的是三个典型的钟形分布的例子。由于两侧的数据不对称,钟形分布出 现偏离对称分布的现象。根据较长的尾所指的方向不同,将偏态可分为正偏(右偏)和负偏 (左偏)两种。左右对称的钟形分布是一种特殊情况,因为自然现象中严格呈现出左右对称 的是非常少见的。对称的钟形分布大多数是属于数据经过处理后的分布形式。其中最典型的 对称钟形分布是正态分布(Nor国al Distribution)。例如将1万人分成250组,每组40人, 每组计算一个平均身高,根据数理统计理论中的中心极值定理,我们可以知道250个组平均 身高数值将表现为一种近似于正态分布的情况 图2.5.6三种钟形分布图 (2)U型分布U型分布的形状与钟形分布相反,靠近中间的变量值分布次数少,靠 近两端的变量值分布次数多,形成“两头大,中间小”的U型分布,反映出某一个社会经济
方法与折线图基本相同,只是在连接各组次数坐标点时应当用平滑曲线。 (4)累计曲线图 累计曲线图的绘制。累计频数(频率)分布图分为向上累计频数(频 率)分布图和向下累计频数(频率)分布图。不论是向上累计还是向下累计均以分组变量为 横轴,以累计频数(频率)为纵轴。在直角坐标系上将各组组距的上限与其相应的累计频数 (频率)构成坐标点,依次用折线(或光滑曲线)相连,即是向上累计曲线。对于向下累计 频数分布图,在直角坐标系上将各组组距下限与其相应累计频数(频率)构成坐标点,依次 用折线(或光滑曲线)相连,即是向下累计分布曲线图。 例如,对于表 2.4.1,以纵坐标表示频数,以横坐标表示分组,做出频数分布的直方图 : 图 2.5.5 频数分布柱状图 (三)频(次)数分布图的类型 当样本量较大,组距较小时,折线图会越来越平滑, 直至成为一条曲线。这种曲线称为次数分布曲线,反映出数据的分布规律。频(次)数分布 图主要有以下三种类型: (1)钟形分布 钟形分布是社会经济现象中最常见的分布形式,具体表现为中间隆起, 两侧逐渐降低。钟形分布表明数据具有集中的趋势,大多数数据集中在中间,越往两端,数 据越少。在远离中心的位置,只有极少数的数据。钟形分布的中间隆起部分称为峰,两侧称 为尾。 图 2.4.6 中所示的是三个典型的钟形分布的例子。由于两侧的数据不对称,钟形分布出 现偏离对称分布的现象。根据较长的尾所指的方向不同,将偏态可分为正偏(右偏)和负偏 (左偏)两种。左右对称的钟形分布是一种特殊情况,因为自然现象中严格呈现出左右对称 的是非常少见的。对称的钟形分布大多数是属于数据经过处理后的分布形式。其中最典型的 对称钟形分布是正态分布(Normal Distribution)。例如将 1 万人分成 250 组,每组 40 人, 每组计算一个平均身高,根据数理统计理论中的中心极值定理,我们可以知道 250 个组平均 身高数值将表现为一种近似于正态分布的情况。 图 2.5.6 三种钟形分布图 (2)U 型分布 U 型分布的形状与钟形分布相反,靠近中间的变量值分布次数少,靠 近两端的变量值分布次数多,形成“两头大,中间小”的 U 型分布,反映出某一个社会经济 0 50 100 150 200 250 300 350 (0,1] (1,2] (2,3] (3,4] (4,5] (5,6] (6,7] (7,8] (8,9] (9,10] (10,11)