
第一章单复变解析函数 11 。x,y+△y)二x,y2+ilim”y千Ay二x, iAy -iu,2+(x,y2 dy dy 所以(:)在:点存在的必要条件是 (1.1.15) 称为柯西-黎曼条件(或方程,记为C-R条件),它是在直角-直角表示下的CR条件。在其 他表示下,它具有不同的形式。C-R条件表明,若函数在一点可导,其实部和虚部不能完全 独立.例如w=人:)==1-y处处不可导。这是因为器=1,器=-1,因面 光≠器不满足CR条件,下面证明 u(x,y),(x,y)在一点z可导(即全微分存在)且满足C-R条件一→f()在点可导 因为dtdu+id起=(货+兴十(4r+器4) “一+能+)停+ 所以-器+器存在。 注意按复变函数在一点微分定义是指d=f'(:)d:,即f(:)在之点可导,而 du十idu一般不是它的微分,除非u,v满足C-R条件。 由上讨论得以下结论, f()=u十iw在一点之可导←→,v在之点可导且满足C-R条件。 导数的几何意义复变函数导数的几何表示为 arg f'(=) +A: arg△r arg Aw :+△:车世+△ 图1.1.6复变函数导数的几何意义 '(lim arg)lim(arg Aw-arg de)
limΔx=0 Δy→0 u(x,y+Δy)-u(x,y) iΔy +ilimΔx=0 Δy→0 v(x,y+Δy)-v(x,y) iΔy =-iu(x,y) y +v(x,y) y 所以f′(z)在z点存在的必要条件是 u x=v y , v x=-u y (1.1.15) 称为柯西 黎曼条件(或方程,记为 CR 条件),它是在直角 直角表示下的 CR 条件。在其 他表示下,它具有不同的形式。CR条件表明,若函数在一点可导,其实部和虚部不能完全 独立。例如 w = f(z)=z = x-iy 处 处 不 可 导。 这 是 因 为 u x = 1,v y =-1,因 而 u x≠v y ,不满足 CR条件。下面证明 u(x,y),v(x,y)在一点z可导(即全微分存在)且满足 CR条件→f(z)在z点可导 因为 dw u,v 可微 du+idv= u x dx+u y ( ) dy +iv x dx+v y ( ) dy CR 条件 u x dx-v x dy+iv x dx+u x ( ) dy = u x+iv ( ) x dz 所以 dw dz =u x+iv x存在。 注意 按复变函数在一点微分定 义是指 dw = f′(z)dz,即 f(z)在z 点 可 导,而 du+idv一般不是它的微分,除非u,v满足 CR条件。 由上讨论得以下结论, f(z)=u+iv在一点z 可导u,v在z 点可导且满足 CR条件。 导数的几何意义 复变函数导数的几何表示为 图116 复变函数导数的几何意义 |f′(z)|= limΔz→0 Δw Δz ,argf′(z)= limΔz→0 (argΔw-argΔz) 第一章 单复变解析函数 11
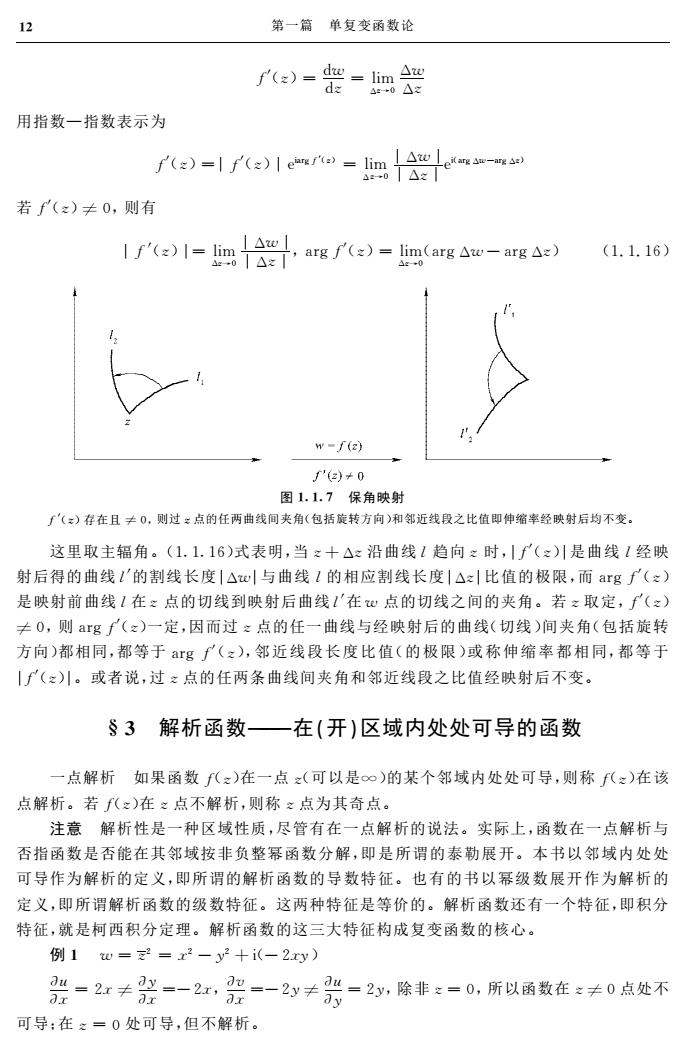
第一篇单复变函数论 f()=架=m智 用指数一指数表示为 ()-f(ero-lim 若(x)≠0,则有 ,L△0I (arg ()im(arg Aw-argA) (1.1.16) w-f(e) ')+0 图1.1.7保角映射 了'(:)存在且≠0,则过:点的任两曲线间夹角(包括旋转方向)和邻近线段之比值即伸缩率经映射后均不变。 这里取主辐角。(1.1.16)式表明,当:十△z沿曲线1趋向之时,|f()川是曲线1经映 射后得的曲线'的割线长度|△与曲线I的相应割线长度|△:比值的极限,而argf(x) 是映射前曲线1在:点的切线到映射后曲线'在心点的切线之间的夹角。若:取定,∫(:) ≠0,则argf(z)一定,因而过:点的任一曲线与经映射后的曲线(切线)间夹角(包括旋转 方向)都相同,都等于g了(z),邻近线段长度比值(的极限)或称伸缩率都相同,都等于 |f(z)川。或者说,过z点的任两条曲线间夹角和邻近线段之比值经映射后不变。 §3解析函数一在(开)区域内处处可导的函数 一点解析如果函数(:)在一点(可以是∞)的某个邻域内处处可导,则称八:)在该 点解析。若()在之点不解析,则称之点为其奇点。 注意解析性是一种区域性质,尽管有在一点解析的说法。实际上,函数在一点解析与 否指函数是否能在其邻域按非负整幂函数分解,即是所谓的泰勒展开。本书以邻域内处处 可导作为解析的定义,即所谓的解析函数的导数特征。也有的书以幂级数展开作为解析的 定义,即所谓解析函数的级数特征。这两种特征是等价的。解析函数还有一个特征,即积分 特征,就是柯西积分定理。解析函数的这三大特征构成复变函数的核心。 例1w=2=x2-y2+i(-2xy) 器-2≠器-2,器-2y≠器-2,除非-0,所以函最在:≠0点处不 可导:在之=0处可导,但不解析
f′(z)=dw dz =limΔz→0 Δw Δz 用指数—指数表示为 f′(z)=|f′(z)|eiargf′(z) =limΔz→0 |Δw| |Δz|ei (argΔw-argΔz) 若f′(z)≠0,则有 |f′(z)|=limΔz→0 |Δw| |Δz|,argf′(z)=limΔz→0 (argΔw-argΔz) (1.1.16) 图117 保角映射 f′(z)存在且 ≠0,则过z点的任两曲线间夹角(包括旋转方向)和邻近线段之比值即伸缩率经映射后均不变。 这里取主辐角。(1116)式表明,当z+Δz沿曲线l趋向z 时,|f′(z)|是曲线l经映 射后得的曲线l′的割线长度|Δw|与曲线l的相应割线长度|Δz|比值的极限,而argf′(z) 是映射前曲线l在z 点的切线到映射后曲线l′在w 点的切线之间的夹角。若z取定,f′(z) ≠0,则argf′(z)一定,因而过z点的任一曲线与经映射后的曲线(切线)间夹角(包括旋转 方向)都相同,都等于argf′(z),邻 近 线 段 长 度 比 值(的 极 限)或 称 伸 缩 率 都 相同,都 等 于 |f′(z)|。或者说,过z点的任两条曲线间夹角和邻近线段之比值经映射后不变。 §3 解析函数———在(开)区域内处处可导的函数 一点解析 如果函数f(z)在一点z(可以是∞)的某个邻域内处处可导,则称f(z)在该 点解析。若f(z)在z点不解析,则称z点为其奇点。 注意 解析性是一种区域性质,尽管有在一点解析的说法。实际上,函数在一点解析与 否指函数是否能在其邻域按非负整幂函数分解,即是所谓的泰勒展开。本书以邻域内处处 可导作为解析的定义,即所谓的解析函数的导数特征。也有的书以幂级数展开作为解析的 定义,即所谓解析函数的级数特征。这两种特征是等价的。解析函数还有一个特征,即积分 特征,就是柯西积分定理。解析函数的这三大特征构成复变函数的核心。 例1 w =z2 =x2 -y2 +i (-2xy) u x=2x ≠y x=-2x,v x=-2y≠u y=2y,除非z=0,所以函数在z≠0点处不 可导;在z=0处可导,但不解析。 21 第一篇 单复变函数论

第一章单复变解析函数 13 区域解析若函数八x)在(开)区域D内一切点处都解析,则称它在区域D内解析。 在开区域内解析等价于处处可导,但在闭区域上处处可导并不能保证在该闭区域上 解析。 函数解析性与奇异性之判断判断函数的解析性和奇异性是复变函数的重要内容。其 判断法则如下: (1)基本法则(即普适法则)从导数原始定义,或从C-R方程,例如=u+i,, 可微且满足C-R方程。 (2)特殊法则(即导出法则)根据解析函数的运算法则可导出以下法则: (2.1)解析函数经四则运算后其解析性不变,但作除法时,分母为零的点可能是例外。 (2.2)解析函数的复合函数,其解析性不变。确切地说,若=g(z)在之=0点解析, f()在o=g(o)处解析,则f(g(:)在:=o点解析。 根据基本法则易知,e在:≠∞处解析,乏处处不解析。根据导出法则知(m≥0整 数),cos,十e等在x≠∞处解析。 例2tan=n三在cos≠0处解析,即在:≠受十k,k=0(土1)士o∞处解析。 cos 例3 sin2+e-可 可以看成一个复合函数w=ge)。十:w)=如w=in十因sinw在 0≠∞解析,而g(:)的奇点由2+之一1=0决定,所以在:≠二1去5处函数解析。 倒4三-2十1=:一1,所以在:≠∞处解析。 之-1 解析函数与共轭调和函数在区域D内解析函数的实部和虚部不是独立的,它由 一阶偏微分方程组即C-R方程联系着。第二章将证明解析函数的任意高阶导数仍解 析,所以在解析区域内其实部和虚部的任意高阶导数都存在。从C-R方程中分别消去 u和v得 器+-0器+-0 在开区域D内一个实值函数的二阶偏导数存在且连续,又满足拉普拉斯方程,则称该函数 为D内的调和函数。所以在开区域D内解析的函数的实部和虚部皆是调和函数,而且满足 C-R方程。满足C-R方程的两个调和函数称为共轭调和函数(conjugate harmonic functions)。由上讨论可知 f(x)在D内解析←→f(z)实部和虚部为D内共轭调和函数 所以复变函数解析性的要求是很强的,不但其任意阶导数均解析,而且由其实部或者虚部就 可以决定该解析函数(除一个任意纯虚或实常数外),即若一个二元实变数实值函数为调和 函数,则根据C-R方程就可以求出其共轭调和函数,由它们构造一解析函数,即 (或)是D内调和函数心R方程求以或),则(z)=M十在D内解析,具体求法
区域解析 若函数f(z)在(开)区域 D 内一切点处都解 析,则 称 它 在 区 域 D 内 解 析。 在开区域内 解 析 等 价 于 处 处 可 导,但 在 闭 区 域 上 处 处 可 导并不能保证在该闭区域上 解析。 函数解析性与奇异性之判断 判断函数的解析性和奇异性是复变函数的重要内容。其 判断法则如下: (1)基本法则(即普适法则) 从导数原始定义,或从 CR方程,例如 w =u+iv,u,v 可微且满足 CR方程。 (2)特殊法则(即导出法则) 根据解析函数的运算法则可导出以下法则: (21)解析函数经四则运算后其解析性不变,但作除法时,分母为零的点可能是例外。 (22)解析函数的复合函数,其解析性不变。确切地说,若w =g(z)在z=z0 点解析, f(w)在 w0 =g(z0)处解析,则f(g(z))在z=z0 点解析。 根据基本法则易知z,ez 在z≠ ∞ 处解析,z处处不解析。根据导出法则知zn (n≥0整 数),cosz,zn +ez 等在z ≠ ∞ 处解析。 例2 tanz=sinz cosz在cosz≠0处解析,即在z≠ π 2 +kπ,k=0(±1)± ∞ 处解析。 例3 sin z z2 +z-1 可以看成一个复合函数 w =g(z)= z z2 +z-1,f(w)=sinw =sin z z2 +z-1,因sinw在 w ≠ ∞ 解析,而g(z)的奇点由z2 +z-1=0决定,所以在z≠ -1±槡5 2 处函数解析。 例4 z2 -2z+1 z-1 =z-1,所以在z≠ ∞ 处解析。 解 析 函 数 与 共 轭 调 和 函 数 在 区 域 D 内解析函数的实部和虚部不是独立的 ,它 由 一阶偏微分方程组即 CR 方程联系着。第二章将证明解析函数的 任意高阶导数仍解 析 ,所 以 在 解 析 区 域 内 其 实 部 和 虚 部 的 任 意 高 阶 导 数 都 存在。从 CR 方 程 中 分 别 消 去 u和v得 2 u x2 +2 u y2 =0,2 v x2 +2 v y2 =0 在开区域 D 内一个实值函数的二阶偏导数存在且连续,又满足拉普拉斯方程,则称该函数 为D 内的调和函数。所以在开区域D 内解析的函数的实部和虚部皆是调和函数,而且满足 CR方 程。 满 足 CR 方 程 的 两 个 调 和 函 数 称 为 共 轭 调 和 函 数(conjugateharmonic functions)。由上讨论可知 f(z)在 D 内解析f(z)实部和虚部为 D 内共轭调和函数 所以复变函数解析性的要求是很强的,不但其任意阶导数均解析,而且由其实部或者虚部就 可以决定该解析函数(除一个任意纯虚或实常数外),即若一个二元实变数实值函数为调和 函数,则根据 CR方程就可以求出其共轭调和函数,由它们构造一解析函数,即 u(或v)是 D 内调和函数 CR →方程 求v(或u),则f(z)=u+iv在D 内解析,具体求法 第一章 单复变解析函数 31

第一篇单复变函数论 如下: (1)先验证“是否调和函数,即求出其调和区域D: (2)若u是D内调和函数,则根据CR方程求出v,其解为 -d加-”-dr+ay 因被积表达式是全微分,所以积分只与始终点有关而与积分路线无关。基于此,常采 用如下计算技巧:在D内选取一点为积分起点,再选一积分路线,应尽量使积分计算简 单。为防止计算时符号上的混淆,采用大写字母表示积分变量,小写字母表示积分限变 量,即 -器+祭+c (1.1.17) C为任意实常数。 例5已知u=x2一3y2,求以它为实部的解析函数及解析区域。 解(1)验证“是否调和函数。容易证明“在有限复平面上都是调和函数。因此存在 以为实部的解析函数在x≠∞处解析: (2)计算。选择起点和积分路线如图1.1.8, 06xYdx+(3x:-3YidY+c++c 在上,Y=0,所以沿的积分为0,而在4上X=0≤Y≤,所以=(3r- 3Y)dY=3x2y-y2,最后得f=u+im=23+iC. 解析函数与平面无旋场平面无旋场是一个旋度 为零的平面矢量场,此时可用一个称作势函数的量来 表征,例如平面静电场,平面无旋流体场等等都是平面 无旋场。这些场的场量即势函数在无源处满足拉普拉 斯方程,若其二阶偏导数连续,则势函数是调和函数, 因而由它可构造一解析函数f(:),称它为该平面无旋 场的复势。通常选势函数为复势的实部“,其虚部称 为该平面无旋场的力函数,因为v=const恰好就是力 线方程。 图1.1.8积分路线十2 等势线u=cost和力线在∫(z)≠0处正交,这是因为解析函数的实部和虚部所构成 的曲线M=const和=co在f(:)≠0处正交:沿曲线u=o有d=dr+y =0,因(d,dy)是该曲线的切向,所以若(0)≠0,它便是曲线的法向,同样=const 在x点的法向为(器),根据-R条件,(股)(二,)=0,即在:点处两曲线 正交。 例6两互相垂直的带电理想平面导体产生的静电场,它是平面无旋场,已知其势函数
如下: (1)先验证u是否调和函数,即求出其调和区域 D; (2)若u是D 内调和函数,则根据 CR方程求出v,其解为 v=∫ (x,y) dv=∫ (x,y) -u y dx+u x dy 因被积表达式是全微分,所以积分只与始终点有关而与积分路线无关。基于此,常采 用如下计算技巧:在 D 内 选 取 一 点 为 积 分 起 点,再 选 一 积 分 路线,应 尽 量 使 积 分 计 算 简 单。为防止计算时符号 上 的 混 淆,采 用 大 写 字 母 表 示 积 分 变 量,小 写 字 母 表 示 积 分 限 变 量,即 v=∫ (x,y) (x0,y0)-u YdX +u XdY +C (1.1.17) C 为任意实常数。 例5 已知u=x3 -3xy2,求以它为实部的解析函数及解析区域。 解 (1)验证u是否调和函数。容易证明u在有限复平面上都是调和函数。因此存在 以u为实部的解析函数在z ≠ ∞ 处解析; (2)计算v。选择起点和积分路线如图118, v=∫ (x,y) (0,0) 6XYdX +(3X2 -3Y2)dY +C =∫l1 +∫l2 +C 在l1 上,Y =0,所以沿l1 的积分为0,而在l2 上 X =x,0≤Y ≤y,所以∫l2 =∫ y 0 (3x2 - 3Y2)dY =3x2 y-y3,最后得f =u+iv=z3 +iC。 图118 积分路线l1 +l2 解析函数与平面无旋场 平面无旋场是一个旋度 为零的平面矢 量 场,此 时 可 用 一 个 称 作 势 函 数 的 量 来 表征,例如平面静电场,平面无旋流体 场 等 等 都 是 平 面 无旋场。这些场的场量即势函数在无源处满足拉普拉 斯方程,若其二 阶 偏 导 数 连 续,则 势 函 数 是 调 和 函数, 因而由它可构造一解 析 函 数 f(z),称它为该平面无旋 场的复势。通常选势函数为复势的实部u,其虚部v称 为该平面无旋场的力函数,因为v =const恰好就是力 线方程。 等势线u=const和力线在f′(z)≠0处正交,这是因为解析函数的实部和虚部所构成 的 曲线u=const和v=const在f′(z)≠0处正交:沿曲线u=const有du=u x dx+u y dy =0,因(dx,dy)是该曲线的切向,所以若 u x,u ( ) y ≠0,它便是曲线的法向,同样v=const 在z点的法向为 v x,v ( ) y ,根据 CR条件, u x,u ( ) y · v x,v ( ) y =0,即在z点处两曲线 正交。 例6 两互相垂直的带电理想平面导体产生的静电场,它是平面无旋场,已知其势函数 41 第一篇 单复变函数论
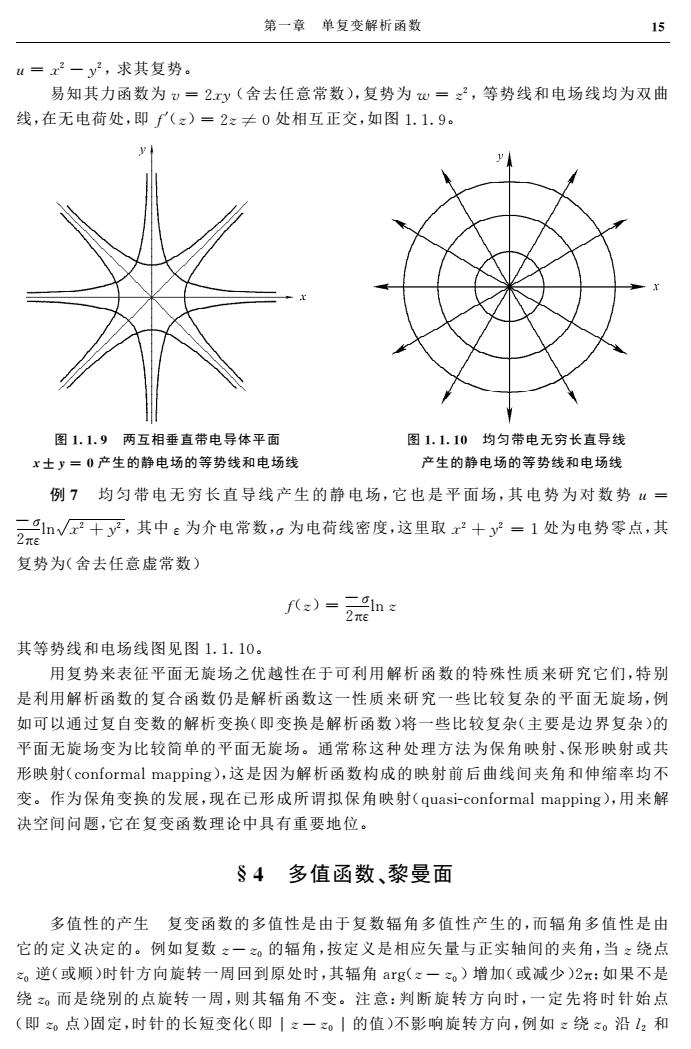
第一章单复变解析函数 4=x2-y2,求其复势 易知其力函数为。=2xy(舍去任意常数),复势为心=2,等势线和电场线均为双曲 线,在无电荷处,即了(:)=2:≠0处相互正交,如图1.1.9。 图1.1.9两互相垂直带电导体平面 图1.1.10均匀带电无穷长直导线 x士y=0产生的静电场的等势线和电场线 产生的静由场的等热线和申场线 例7均匀带电无穷长直导线产生的静电场,它也是平面场,其电势为对数势“= 三1vF十了,中e为介电常数g为电荷线密度,这里取2十-1处为电势零点,其 复势为(舍去任意虚常数)》 其等势线和电场线图见图1.1.10。 用复势来表征平面无旋场之优越性在于可利用解析函数的特殊性质来研究它们,特别 是利用解析函数的复合函数仍是解析函数这一性质来研究一些比较复杂的平面无旋场,例 如可以通过复自变数的解析变换(即变换是解析函数)将一些比较复杂(主要是边界复杂)的 平面无旋场变为比较简单的平面无旋场。通常称这种处理方法为保角映射、保形映射或共 形映射(conformal mapping),这是因为解析函数构成的映射前后曲线间夹角和伸缩率均不 变。作为保角变换的发展,现在已形成所谓拟保角映射(quasi-onformal mapping),用米解 决空间问题,它在复变函数理论中具有重要地位。 §4多值函数、黎曼面 多值性的产生复变函数的多值性是由于复数辐角多值性产生的,而辐角多值性是由 它的定义决定的。例如复数:一。的辐角,按定义是相应矢量与正实轴间的夹角,当:绕点 ,逆(或顺)时针方向旋转一周回到原处时,其辐角ag(:一)增加(或减少)2x:如果不是 绕。而是绕别的点旋转一周,则其辐角不变。注意:判断旋转方向时,一定先将时针始点 (即。点)固定,时针的长短变化(即12一1的值)不影响旋转方向,例如:绕,沿4和
u=x2 -y2,求其复势。 易知其力函数为v=2xy(舍去任意常数),复势为 w =z2,等势线和电场线均为双曲 线,在无电荷处,即f′(z)=2z≠0处相互正交,如图119。 图119 两互相垂直带电导体平面 x±y=0产生的静电场的等势线和电场线 图1110 均匀带电无穷长直导线 产生的静电场的等势线和电场线 例7 均匀带电无穷长直导线产生的静电场,它 也 是 平 面 场,其 电 势 为 对 数 势 u = -σ 2πε ln x2 槡 +y2,其中ε为介电常数,σ为电荷线密度,这里取x2 +y2 =1处为电势零点,其 复势为(舍去任意虚常数) f(z)= -σ 2πε lnz 其等势线和电场线图见图1110。 用复势来表征平面无旋场之优越性在于可利用解析函数的特殊性质来研究它们,特别 是利用解析函数的复合函数仍是解析函数这一性质来研究一些比较复杂的平面无旋场,例 如可以通过复自变数的解析变换(即变换是解析函数)将一些比较复杂(主要是边界复杂)的 平面无旋场变为比较简单的平面无旋场。通常称这种处理方法为保角映射、保形映射或共 形映射(conformalmapping),这是因为解析函数构成的映射前后曲线间夹角和伸缩率均不 变。作为保角变换的发展,现在已形成所谓拟保角映射(quasiconformalmapping),用来解 决空间问题,它在复变函数理论中具有重要地位。 §4 多值函数、黎曼面 多值性的产生 复变函数的多值性是由于复数辐角多值性产生的,而辐角多值性是由 它的定义决定的。例如复数z-z0 的辐角,按定义是相应矢量与正实轴间的夹角,当z绕点 z0 逆(或顺)时针方向旋转一周回到原处时,其辐角arg(z-z0)增加(或减少)2π;如果不是 绕z0 而是绕别的点旋转一周,则其辐角不变。注 意:判 断 旋 转 方 向时,一 定 先 将 时 针 始 点 (即z0 点)固定,时针的长短变化(即|z-z0|的值)不影响旋转方向,例如z绕z0 沿l2 和 第一章 单复变解析函数 51