
6 第一篇单复变函数论 -2=(m-x:)+i(y1-y2) 是一会提-白十”诗十”型 x2十y 乘方它基于乘法 =(x+iy)”= []-m (1.1.5) 其中n为自然数,[受]表示取号的整数部分,e(n)一 1,n为偶数 0,n为奇数 开方是乘方的逆运算。 以上运算都是按直角表示定义的。当然可以用复数的任何一种表示定义。用直角表示 定义这些运算后,在其他表示下相应的结果不难得到,例如在指数表示下,4=n则有 =r"ely =Fe/+,k=0(1)n-1 开方运算是多值运算,这种多值性是辐角多值性引起的。由上可见,乘方和开方运算,用指 数表示比较方便。 对于复数加、乘运算,显然满足结合律、交换律和分配律。复数共轭运算具有如下规律: 士西=士,商=,(月)=爱,2=子,(质)=月 注意最后一式是指集合相等,即E}-)或,k=0(1)m一1) =e,k=0(1)m。 以上定义的复数运算是否合理?实际上,这些运算的定义和普通实数运算完全一样,只 是引进新元素,并利用=一1。因此当复数退化为实数时,其运算结果和实数运算结果相 同,即不发生矛盾,因而这种扩充是合理的,科学的。能否有另一种扩充方法?例如定义复 数相等为实虚部交叉相等。 1=21=次,=x2 这个定义显然不符合扩充三原则,因为复数退化为实数时,即出=为=0时,就发生矛盾, 除非x1=x2=O。复数还可以扩充,如扩充为四元数(quaternion),还可以继续扩充为克利 福德(Clifford)代数o]。 复数乘法与矢量乘法如果复数用几何表示,那么复数相等、相加以及与实数相乘的定 义和矢量的相应运算相同,但复数的乘法运算既不同于矢量的点乘,也不同于矢量的叉乘
z1 -z2 =(x1 -x2)+i (y1 -y2) z1 z2 =x1 +iy1 x2 +iy2 =(x1x2 +y1y2)+i (-x1y2 +y1x2) x2 2 +y2 2 乘方 它基于乘法 zn =(x+iy)n = ∑ n k=0 ( )n k (iy)k xn-k = ∑ [ ]n 2 k=0 (-1)k n ( ) 2ky2k xn-2k +i ∑ [ ]n 2 -ε(n) k=0 (-1)k n ( ) 2k+1y2k+1 xn-2k-1 (1.1.5) 其中n为自然数,n [ ]2 表示取n 2的整数部分,ε(n)= 1,n为偶数 {0,n为奇数 开方是乘方的逆运算。 以上运算都是按直角表示定义的。当然可以用复数的任何一种表示定义。用直角表示 定义这些运算后,在其他表示下相应的结果不难得到,例如在指数表示下,zk =rkeiφk 则有 z1·z2 =r1r2ei (φ1+φ2) zn =rn einφ n 槡z = n 槡rei (argz/n+kπ/n),k=0(1)n-1 开方运算是多值运算,这种多值性是辐角多值性引起的。由上可见,乘方和开方运算,用指 数表示比较方便。 对于复数加、乘运算,显然满足结合律、交换律和分配律。复数共轭运算具有如下规律: z1 ±z2 =z1 ±z2,z1z2 =z1z2, z1 ( ) z2 =z1 z2 ,zn =zn, n ( ) 槡z = n 槡z 注意 最 后 一 式 是 指 集 合 相 等,即 n { } 槡z = {n 槡z}或 {e-i (argz+2kπ) n ,k = 0(1)n - 1} ={ei (argz+2k′π) n ,k′ =0(1)n}。 以上定义的复数运算是否合理?实际上,这些运算的定义和普通实数运算完全一样,只 是引进新元素i,并利用i2 =-1。因此当复数退化为实数时,其运算结果和实数运算结果相 同,即不发生矛盾,因而这种扩充是合理的,科学的。能否有另一种扩充方法?例如定义复 数相等为实虚部交叉相等。 z1 =z2x1 =y2,y1 =x2 这个定义显然不符合扩充三原则,因为复数退化为实数时,即y1 =y2 =0时,就发生矛盾, 除非x1 =x2 =0。复数还可以扩充,如扩充为四元数(quaternion),还可以继续扩充为克利 福德(Clifford)代数[10]。 复数乘法与矢量乘法 如果复数用几何表示,那么复数相等、相加以及与实数相乘的定 义和矢量的相应运算相同,但复数的乘法运算既不同于矢量的点乘,也不同于矢量的叉乘, 6 第一篇 单复变函数论

第一章单复变解析函数 7 相应的是一种新的矢量乘法。所以在这种复数运算定义下,只对加法和与实数的乘法而言, 复数运算结果和矢量运算结果相同,此时称为复数和矢量对实系数线性运算同构,即对实系 数线性运算而言,复数等同于矢量。 在电工学里,交流单频正弦电压常用复数表示, 也可以用平面矢量表示。这样电压不就是矢量了? 当然不是,因为这种等效性是有条件的,即对实系数 线性运算它们才等效。 复数的初等超越运算定义指数运算 ee旦ed。eiw (1.1.6) 它是周期为2的虚周期函数。对数运算为其逆运算, 图1.1.3复数乘法的几何表示 Ln。=In I+iArg 当取主辐角时,对数用ln表示,即lnz=ln|z|十iargz。同样,在不会引起混淆的地方, 都用lnz表示。 定义三角运算 in:会e,cos:+e 21 2 (1.1.7) ta an coti sin 反三角运算为三角运算的逆运算。 因为三角运算用指数运算定义的,所以反三角运算必将可以用反指数即对数来表示,例如 arcsin =iln(1-+i)=iln(1--i) (1.1.8) 双曲运算定义为sh之e一e二,ch之会+e二 而任意幂运算定义为 Aesn: (1.1.9) 其中a为任意复数。 以上初等超越运算的扩充是合理的,因为它符合扩充三原则。例如,当,α皆为实数 时,按(1.1.9)式定义的运算结果和相应的实数运算结果相同。 §2复变函数及其导数 (单)复变函数复变数:在复平面上的点集D上取每个值时,按照一定规律相应地有 一个或几个复数与之对应。这种对应规律(或关系)称为函数关系,记作,称心f(:) 是自变数:的(单值或多值)函数。点集D称为该函数的定义集合,心的取值构成该函数的 取值集合 复变函数表示因为自变数和因变数各有多种表示,所以复变函数表示就更加多样化
相应的是一种新的矢量乘法。所以在这种复数运算定义下,只对加法和与实数的乘法而言, 复数运算结果和矢量运算结果相同,此时称为复数和矢量对实系数线性运算同构,即对实系 图113 复数乘法的几何表示 数线性运算而言,复数等同于矢量。 在电工学里,交流单频正弦电压常用复数表示, 也可以 用 平 面 矢 量 表 示。这 样 电 压 不 就 是 矢 量 了? 当然不是,因为这种等效性是有条件的,即对实系数 线性运算它们才等效。 复数的初等超越运算 定义指数运算 ez = △ ex·eiy (1.1.6) 它是周期为2πi的虚周期函数。对数运算为其逆运算, Lnz=ln|z|+iArgz 当取主辐角时,对数用ln表示,即lnz=ln|z|+iargz。同样,在不会引起混淆的地方, 都用lnz表示。 定义 三角运算 sinz= △ eiz -e-iz 2i ,cosz= △ eiz +e-iz 2 tanz= △ sinz cosz ,cotz= △ cosz sinz (1.1.7) 反三角运算为三角运算的逆运算。 因为三角运算用指数运算定义的,所以反三角运算必将可以用反指数即对数来表示,例如 arcsinz=-iln(槡1-z2 +iz)=iln(槡1-z2 -iz) (118) 双曲运算定义为shz= △ ez -e-z 2 ,chz= △ ez +e-z 2 , 而任意幂运算定义为 zα = △ eαlnz (1.1.9) 其中α为任意复数。 以上初等超越运算的扩充是合理的,因为它符合扩充三原则。例如,当z,α皆为实数 时,按(119)式定义的运算结果和相应的实数运算结果相同。 §2 复变函数及其导数 (单)复变函数 复变数z在复平面上的点集D 上取每个值时,按照一定规律相应地有 一个或几个复数 w 与之对应。这种对应规律(或关系)称为函数关系,记作f,称 w =f(z) 是自变数z的(单值或多值)函数。点集 D 称为该函数的定义集合,w 的取值构成该函数的 取值集合。 复变函数表示 因为自变数和因变数各有多种表示,所以复变函数表示就更加多样化。 第一章 单复变解析函数 7
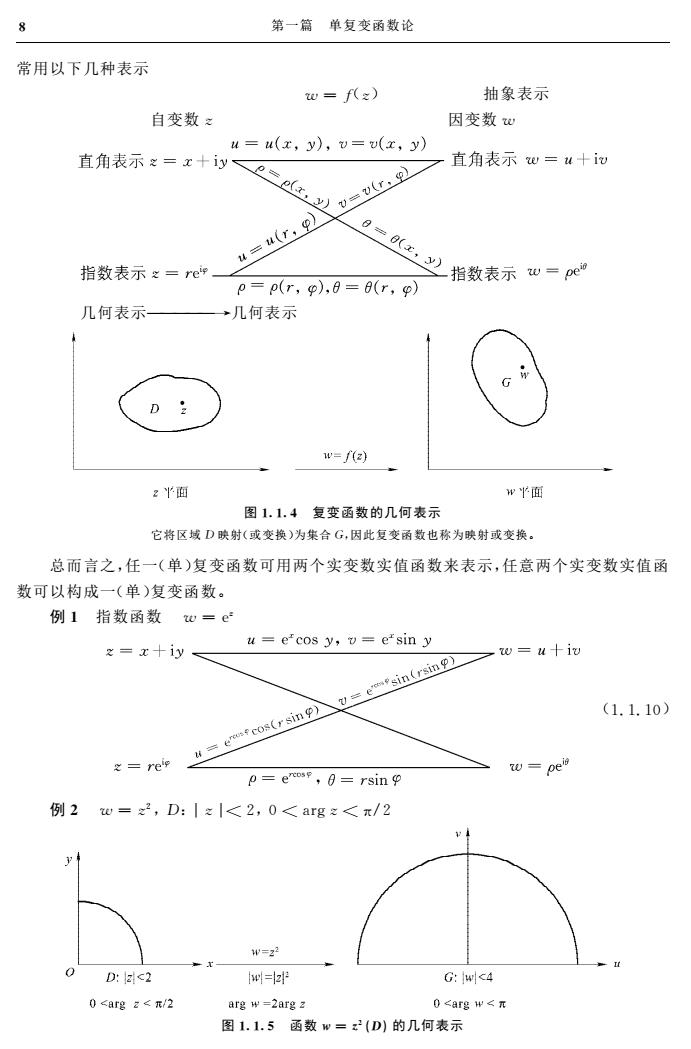
8 第一篇单复变函数论 常用以下几种表示 w=f() 抽象表示 自变数: 因变数心 直角表示x=十订Qc 4=u(x,y),v=(x,y 一直角表示w=w十i记 =(r,】 指数表示=re p=p(r,p),8=(r,p) 几何表示 几何表示 D w=f(2) 2Y面 w半面 图1.1.4复变函数的几何表示 它将区城D映射(或变换)为集合G,因此复变函数也称为映射或变换。 总而言之,任一(单)复变函数可用两个实变数实值函数来表示,任意两个实变数实值函 数可以构成一(单)复变函数。 例1指数函数地=e =x十iy u=e'cos y,=e'sin y >w=u十iw 4=etco8(rsing)入=e=fsin(sinp) (1.1.10) 之=rep p=eros,0=rsin w=peis 例2=2,D:|z|<2,0<arg<π/2 v i y w=2 0D:z<2 w= G:w<4 0<argz<元/2 arg w=2arg 2 0<argw<π 图1.1.5函数w=2(D)的几何表示
常用以下几种表示 w =f(z) 抽象表示 自变数z 因变数 w → 几何表示 几何表示 图114 复变函数的几何表示 它将区域 D 映射(或变换)为集合G,因此复变函数也称为映射或变换。 总而言之,任一(单)复变函数可用两个实变数实值函数来表示,任意两个实变数实值函 数可以构成一(单)复变函数。 例1 指数函数 w =ez (1.1.10) 例2 w =z2,D:|z|<2,0<argz<π/2 图115 函数w =z2(D)的几何表示 8 第一篇 单复变函数论

第一章单复变解析函数 9 极限与连续已定义了基本关系和初等运算,接着要定义复数间距离,基于距离定义, 就可以定义高等运算了,即极限运算及基于极限运算的连续、微商、积分、无穷级数和无穷乘 积等运算。整个复变函数,都是在作这种扩充过程,这种扩充需且只需遵循扩充三原则。 距离定义两复数间距离可定义为两者之差的模 d(,)=|-21 (1.1.11) 有了距离定义,可以定义邻域、区域。 一点邻域以0点为心,e为半径的一个圆内部|之一|<e称为z,点的e邻域:当 =∞时称1x一a|>R(a为任意有限复数)为无穷远点的R邻域。 内点、外点、边界点和极限点 内点和外点如果存在的一个邻域,其内的点都属于(都不属于)D,则称之=。是 D的内点(外点)。 边界点它的任何一个邻域既有D内的点也有D外的点,则称它为D的边界点。 极限点它的任何一个邻域内都有无穷多个点属于D,则称该点为点集D的极限点。 开、闭区域凡具有开集性(即由其全部内点构成)和连通性(即其中任意两点都可以用 属于这个集合的一折线连结起来)的点集称为开区域,简称区域:具有闭集性(即由其全部内 点和全部边界点构成)和连通性的点集称为闭区域。 单、复通区域在区域内部无论怎样画一条闭曲线,闭曲线所围部分属于它,则称此区 域为单(连)通区域,否则称为复(连)通区域。 有界、无界区域若有一个有限圆将之包围的区域称为有界区域,否则称为无界区域。 现在定义极限 im/x)=a一,im。1fx)-al=0 (1.1.12) 因1之-=x-+(y-w-一0一x→,y→% |f(z)-a|=√(u-Rea+(o-lmaF-→0。→w→Rea,v→lma 所以复变函数的极限定义可归结为两个实变数实值函数的极限。极限定义1.1.12表明,只 有当:在复平面上沿任意路径趋向于。时函数都有极限且都相等时,才称:趋向于。函 数有极限,所以按(1.1.11)式定义的距离米定义的极限要求是很高的,例如,极限1m三= l四e:不存在。 连续若1imf(:)=(xo),则称函数f(:)在连续。同样,一单复变函数的连续性 等效于两实变数实值函数的连续性, limf()=lim[u(r,y)+id,y)]=(ro)+iy) 导数设:为有限点,若极限 m:+)- (1.1.13)
极限与连续 已定义了基本关系和初等运算,接着要定义复数间距离,基于距离定义, 就可以定义高等运算了,即极限运算及基于极限运算的连续、微商、积分、无穷级数和无穷乘 积等运算。整个复变函数,都是在作这种扩充过程,这种扩充需且只需遵循扩充三原则。 距离定义 两复数间距离可定义为两者之差的模 d(z1,z2)=|z1 -z2| (1.1.11) 有了距离定义,可以定义邻域、区域。 一点邻域 以z0 点为心,ε为半径的一个圆内部|z-z0|<ε称为z0 点的ε邻域;当z0 = ∞ 时称|z-α|>R(α为任意有限复数)为无穷远点的R 邻域。 内点、外点、边界点和极限点 内点和外点 如果存在z0 的一个邻域,其内的点都属于(都不属于)D,则称z =z0 是 D 的内点(外点)。 边界点 它的任何一个邻域既有 D 内的点也有D 外的点,则称它为 D 的边界点。 极限点 它的任何一个邻域内都有无穷多个点属于 D,则称该点为点集 D 的极限点。 开、闭区域 凡具有开集性(即由其全部内点构成)和连通性(即其中任意两点都可以用 属于这个集合的一折线连结起来)的点集称为开区域,简称区域;具有闭集性(即由其全部内 点和全部边界点构成)和连通性的点集称为闭区域。 单、复通区域 在区域内部无论怎样画一条闭曲线,闭曲线所围部分属于它,则称此区 域为单(连)通区域,否则称为复(连)通区域。 有界、无界区域 若有一个有限圆将之包围的区域称为有界区域,否则称为无界区域。 现在定义极限 limz→z0 f(z)=α lim |z-z0|→0 |f(z)-α|=0 (1.1.12) 因 |z-z0|= (x-x0)2 槡 +(y-y0) → 2 0x →x0,y →y0 |f(z)-α|= (u-Reα)2 槡 +(v-Imα) → 2 0u→ Reα,v→Imα 所以复变函数的极限定义可归结为两个实变数实值函数的极限。极限定义1112表明,只 有当z在复平面上沿任意路径趋向于z0 时函数都有极限且都相等时,才称z趋向于z0 函 数有极限,所以按(1111)式定义的距离来定义的极限要求是很高的,例如,极限limz→0 z z = limz→0 ei2argz 不存在。 连续 若limz→z0 f(z)=f(z0),则称函数f(z)在z0 连续。同样,一单复变函数的连续性 等效于两实变数实值函数的连续性, limz→z0 f(z)=limx→x0 y→y0 [u(x,y)+iv(x,y)]=u(x0,y0)+iv(x0,y0) 导数 设z为有限点,若极限 limΔz→0 f(z+Δz)-f(z) Δz (1.1.13) 第一章 单复变解析函数 9

第一篇单复变函数论 存在,则称函数e=八x)在:点可导,极限值称为函数在:点的导数或微商,记为(:)或 长而d=了八:称为函数在:点的微分。 当:=四时,则可适过变换:-亡将它变为有限点5若函数g)-日女)在 5=5。可导,则称f(z)在:=∞可导,其导数定义为f(∞)=g'(5)。易证,这个定义与0 的选择无关,一般选5。=0。 导数的运算法则(单)复变函数导数和单实变数实值函数的导数运算法则完全类 似,如 (1)线性运算(af(x)+g(z)y=af+g (2)乘积(fg)'=fg+fg 3)商(}=二区 (4)反函数若心=f(:),之=g(心),双方单值 f(x)=1 du (5)复合函数 e)=影柴 复变函数可导条件复变函数在一点的可导性能否归结为两个实变数实值函数在该点 的可导性?例如w=f八z)=u十iw在一点z可导?u,o在该点可导。 作为二元函数(x,y),(x,y),其可导含义是指存在全微分 d加一2+4,d加-2r+器ay 所以上面的问题归结为f(之)存在<d,du存在。 容易证明,若f(x)在之点存在,du,dv一定存在,但反过来说,两个任意的(可以毫无 关系的,独立的)在一点可导的实二元实值函数是否一定能构成一个在该点可导的复变函数 呢?回答是否定的。原因是复变函数可导定义要求是很严的,要求沿任意方向△:→0,比值 公的极限存在且极限值皆相等,制如要求分别沿:和y方向△:0时,极限存在且相等, m=a2-@-m f(z+△:)-f(:) (1.1.14) △ △之 其左式和右式的极限分别是 雲+22+:t-2 △x -8 Ar dx
存在,则称函数 w =f(z)在z点可导,极限值称为函数在z点的导数或微商,记为f′(z)或 df dz,而df =f′(z)dz称为函数在z 点的微分。 当z= ∞ 时,则可通过变换z= 1 ζ-ζ0 将它变为有限点ζ0,若函数g(ζ)=f 1 ( ) ζ-ζ0 在 ζ=ζ0 可导,则称f(z)在z= ∞ 可导,其导数定义为f′(∞)=g′(ζ0)。易证,这个定义与ζ0 的选择无关,一般选ζ0 =0。 导数的运算法 则 (单)复 变 函 数 导 数 和 单 实 变 数 实 值函数的导数运算法则完全类 似,如 (1)线性运算 (αf(z)+βg(z))′ =αf′+βg′ (2)乘积 (fg)′ =f′g+fg′ (3)商 f ( ) g ′ =f′g-fg′ g2 (4)反函数 若 w =f(z),z=g(w),双方单值 f′(z)= 1 g′(w) 即 dw dz = 1 dz dw (5)复合函数 d dz f(g(z))=df dg dg dz 复变函数可导条件 复变函数在一点的可导性能否归结为两个实变数实值函数在该点 的可导性?例如 w =f(z)=u+iv在一点z 可导 ?u,v在该点可导。 作为二元函数u(x,y),v(x,y),其可导含义是指存在全微分 du=u x dx+u y dy,dv=v x dx+v y dy 所以上面的问题归结为f′(z)存在?du,dv存在。 容易证明,若f′(z)在z点存在,du,dv一定存在,但反过来说,两个任意的(可以毫无 关系的,独立的)在一点可导的实二元实值函数是否一定能构成一个在该点可导的复变函数 呢?回答是否定的。原因是复变函数可导定义要求是很严的,要求沿任意方向 Δz→0,比值 Δf Δz的极限存在且极限值皆相等,例如要求分别沿x和y 方向 Δz→0时,极限存在且相等, lim Δz=Δx→0 f(z-Δz)-f(z) Δz = lim Δz=iΔy→0 f(z+Δz)-f(z) Δz (1114) 其左式和右式的极限分别是 limΔx→0 Δy=0 u(x+Δx,y)-u(x,y) Δx +ilimΔx→0 Δy=0 v(x+Δx,y)-v(x,y) Δx =u(x,y) x +iv(x,y) x 01 第一篇 单复变函数论