
第8章热力学平斷态 §8.1热力学系统平衡态 §8.2热力学第零定律温度和温标 §8.3理想气体温标和状态方程 §8.4理想气体微观模型 压强和温度的 统计意义 §8.5能量均分定理 §8.6麦克斯韦速率和速度分布 §8.7玻尔兹曼分布 §8.8量子统计分布简介
§8.1 热力学系统 平衡态 第 8 章 热力学平衡态 §8.2 热力学第零定律 温度和温标 §8.3 理想气体温标和状态方程 §8.4 理想气体微观模型 压强和温度的 统计意义 §8.5 能量均分定理 §8.6 麦克斯韦速率和速度分布 §8.7 玻尔兹曼分布 §8.8 量子统计分布简介

§8.6麦克斯韦速率和速度分布 一、分子速率分布函数 叶△v 0 v>y+△y内的分子数:△W AN f(v)Ay (当△v较小时) N △W dN 定义:f(v)=lim A0N△y Ndv 代表速率v附近单位速率区间内分子数占总数比率
一、 分子速率分布函数 §8.6 麦克斯韦速率和速度分布 +→ Δvvv 内的分子数: ΔN 代表速率 v 附近单位速率区间内分子数占总数比率 定义: vN N vN N vf v d d lim)( 0 = Δ Δ = →Δ o v v + Δ v v vvf N N Δ∝ Δ )( (当 Δv 较小时)
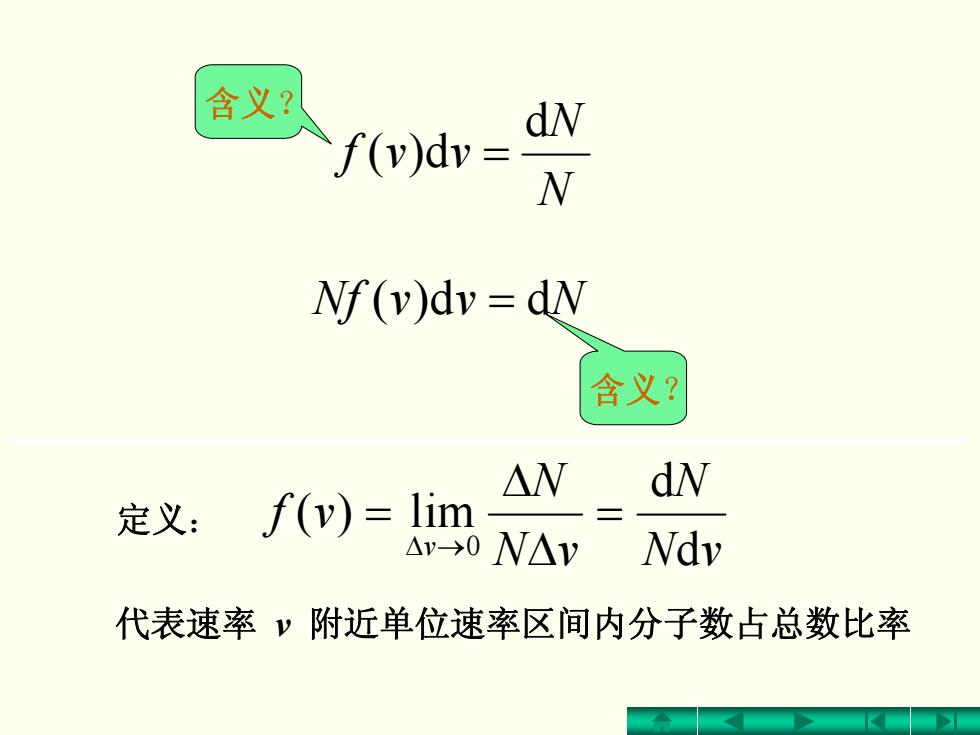
含义? dN f(v)dv W Nf(v)dv dN 含义? △W dN 定义:f(v)=lim Av-0N△y Ndv 代表速率y附近单位速率区间内分子数占总数比率
N N vvf d d)( = 含义? = dd)( NvvNf 含义? 代表速率 v 附近单位速率区间内分子数占总数比率 定义: vN N vN N vf v d d lim)( 0 = ΔΔ = →Δ
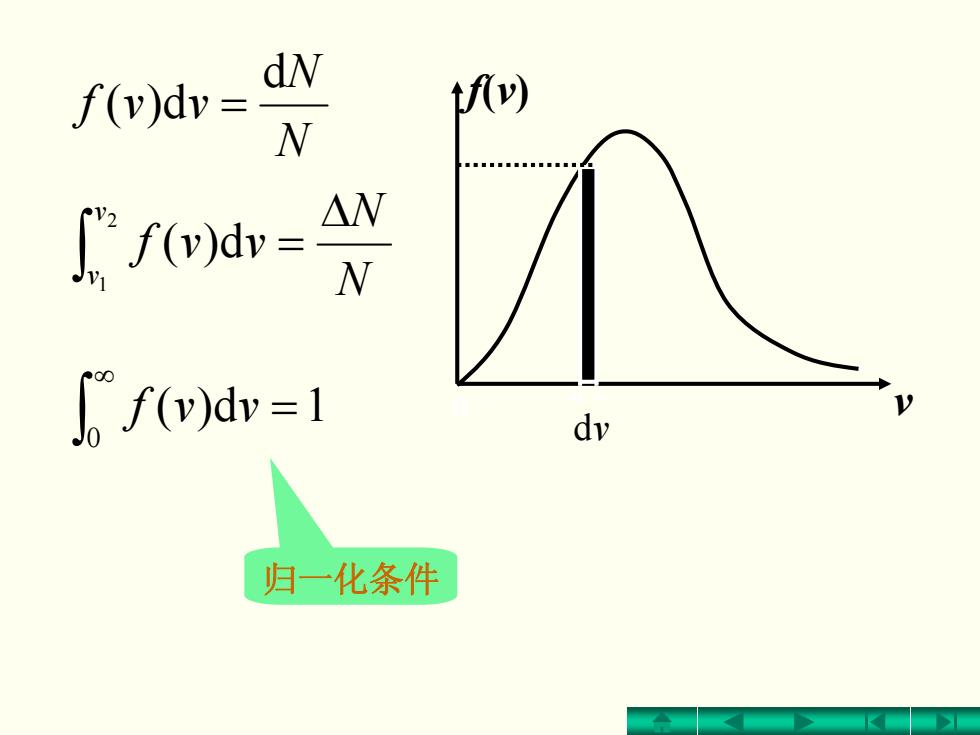
dN f(v)dv= iAv) N ["f(v)dv= △W W f(v)dv=1 dv 归一化条件
v N N vvf v v Δ = ∫ 21 d)( 1d)( 0 = ∫∞ vvf 归一化条件 N N vvf d d)( = o f(v) dv

求平均值: 。一 W =听)d .-w
求平均值: N Nv v ∫∞ = 0 d ∫∞ = 0 d)( vvvf N Nv v ∫∞ = 0 2 2 d ∫∞ = 0 2 d)( vvfv