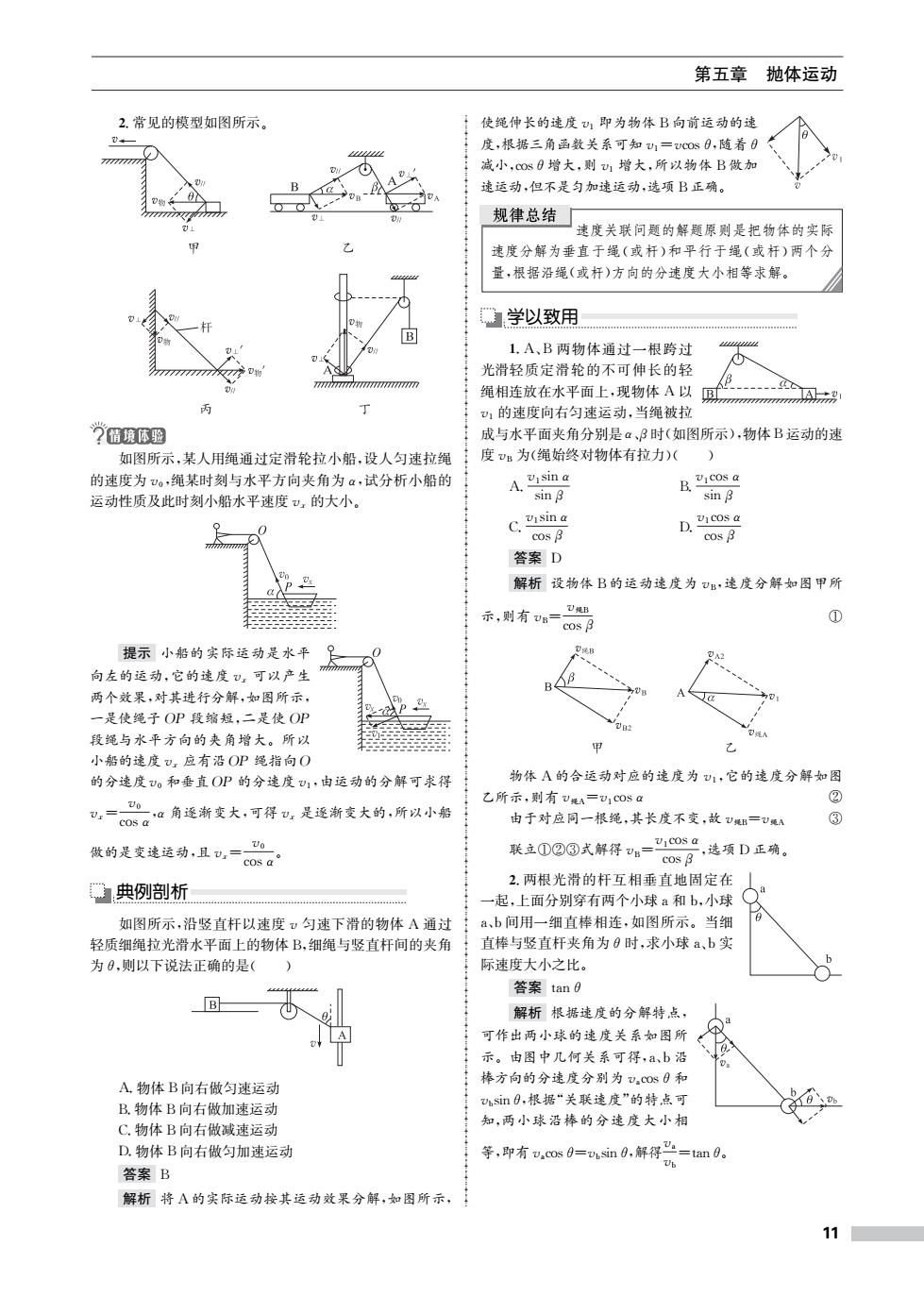
第五章 抛体运动 2.常见的模型如图所示。 使绳伸长的速度1即为物体B向前运动的速 度,根据三角函数关系可知U1=vcOs0,随着0 777777777 减小,cOs0增大,则1增大,所以物体B做加 B 速运动,但不是匀加速运动,选项B正确。 规律总结 速度关联问题的解题原则是把物体的实际 7 速度分解为垂直于绳(或杆)和平行于绳(或杆)两个分 量,根据沿绳(或杆)方向的分速度大小相等求解。 学以致用 1.A、B两物体通过一根跨过 光滑轻质定滑轮的不可伸长的轻 mnmmmm 绳相连放在水平面上,现物体A以 丙 丁 1的速度向右匀速运动,当绳被拉 ?情境体宠 成与水平面夹角分别是α、3时(如图所示),物体B运动的速 如图所示,某人用绳通过定滑轮拉小船,设人匀速拉绳 度s为(绳始终对物体有拉力)( ) 的速度为v。,绳某时刻与水平方向夹角为α,试分析小船的 A.Visin a B.Vicos a 运动性质及此时刻小船水平速度,的大小。 sinB sin B C.Vsin a D.vcosa cos B cos B 答案D 解析设物体B的运动速度为B,速度分解如图甲所 示,则有g=想 ΓcosB 0 提示小船的实际运动是水平 向左的运动,它的速度:可以产生 两个效果,对其进行分解,如图所示, 一是使绳子OP段缩短,二是使OP 段绳与水平方向的夹角增大。所以 甲 小船的速度v应有沿OP绳指向O 的分速度v。和垂直OP的分速度U1,由运动的分解可求得 物体A的合运动对应的速度为1,它的速度分解如图 乙所示,则有U绳A=U1C0Sa ② ,α角逐渐变大,可得v是逐渐变大的,所以小船 cos a 由于对应同一根绳,其长度不变,故V绳B=V绳A 做的是变速运动,且v,= 联立①②③式解得t%=o cos B ,选项D正确。 cos a 2.两根光滑的杆互相垂直地固定在 典例剖析 起,上面分别穿有两个小球a和b,小球 如图所示,沿竖直杆以速度匀速下滑的物体A通过 a、b间用一细直棒相连,如图所示。当细 轻质细绳拉光滑水平面上的物体B,细绳与竖直杆间的夹角 直棒与竖直杆夹角为0时,求小球a、b实 为0,则以下说法正确的是( 际速度大小之比。 答案tan日 B 解析根据速度的分解特点, 可作出两小球的速度关系如图所 示。由图中几何关系可得,a、b沿 D A物体B向右做匀速运动 棒方向的分速度分别为v.c0s日和 B.物体B向右做加速运动 vsin0,根据“关联速度”的特点可 C.物体B向右做减速运动 知,两小球沿棒的分速度大小相 D.物体B向右做匀加速运动 等,即有u,cos0=in,解得头=an0。 Uh 答案B 解析将A的实际运动按其运动效果分解,如图所示, 11
第五章 抛体运动 2.常见的模型如图所示。 如图所示,某人用绳通过定滑轮拉小船,设人匀速拉绳 的速度为v0,绳某时刻与水平方向夹角为α,试分析小船的 运动性质及此时刻小船水平速度vx 的大小。 提示 小船的实际运动是水平 向左的运动,它的速度vx 可以产生 两个效果,对其进行分解,如图所示, 一是使绳子OP 段缩短,二是使OP 段绳与水平方向的夹角增大。所以 小船的速度vx 应有沿OP 绳指向O 的分速度v0 和垂直OP 的分速度v1,由运动的分解可求得 vx= v0 cosα ,α角逐渐变大,可得vx 是逐渐变大的,所以小船 做的是变速运动,且vx= v0 cosα 。 典例剖析 如图所示,沿竖直杆以速度v 匀速下滑的物体 A 通过 轻质细绳拉光滑水平面上的物体B,细绳与竖直杆间的夹角 为θ,则以下说法正确的是( ) A.物体B向右做匀速运动 B.物体B向右做加速运动 C.物体B向右做减速运动 D.物体B向右做匀加速运动 答案 B 解析 将A的实际运动按其运动效果分解,如图所示, 使绳伸长的速度v1 即为物体B向前运动的速 度,根据三角函数关系可知v1=vcosθ,随着θ 减小,cosθ增大,则v1 增大,所以物体B做加 速运动,但不是匀加速运动,选项B正确。 速度关联问题的解题原则是把物体的实际 速度分解为垂直于绳(或杆)和平行于绳(或杆)两个分 量,根据沿绳(或杆)方向的分速度大小相等求解。 学以致用 1.A、B两物体通过一根跨过 光滑轻质定滑轮的不可伸长的轻 绳相连放在水平面上,现物体 A以 v1 的速度向右匀速运动,当绳被拉 成与水平面夹角分别是α、β时(如图所示),物体B运动的速 度vB 为(绳始终对物体有拉力)( ) A. v1sinα sinβ B. v1cosα sinβ C. v1sinα cosβ D. v1cosα cosβ 答案 D 解析 设物体B的运动速度为vB,速度分解如图甲所 示,则有vB= v绳B cosβ ① 物体 A的合运动对应的速度为v1,它的速度分解如图 乙所示,则有v绳A=v1cosα ② 由于对应同一根绳,其长度不变,故v绳B=v绳A ③ 联立①②③式解得vB= v1cosα cosβ ,选项D正确。 2.两根光滑的杆互相垂直地固定在 一起,上面分别穿有两个小球a和b,小球 a、b间用一细直棒相连,如图所示。当细 直棒与竖直杆夹角为θ时,求小球a、b实 际速度大小之比。 答案 tanθ 解析 根据速度的分解特点, 可作出两小球的速度关系如图所 示。由图中几何关系可得,a、b沿 棒方向的分速度分别为vacosθ和 vbsinθ,根据“关联速度”的特点可 知,两小球沿棒的分速度大小相 等,即有vacosθ=vbsinθ,解得 va vb =tanθ。 11

物理 必修 第二册 配人教版 随堂训练 1.对于两个分运动的合运动,下列说法正确的是( 4.如图所示,中间有孔的物块A套在光滑的 A.合运动的速度大小等于两个分运动的速度大小之和 竖直杆上,通过滑轮用不可伸长的轻绳将 B.合运动的速度一定大于某一个分运动的速度 物体拉着匀速向上运动。则关于拉力F C.合运动的方向就是物体实际运动的方向 及拉力作用点的移动速度,下列说法正确 D.由两个分速度的大小就可以确定合速度的大小 的是() 答案C A.F不变、v不变 解析根据平行四边形定则知,邻边表示两个分运动的速 B.F增大v不变 度,合运动的速度的大小和方向可由对角线表示,由几何关 C.F增大、v增大 系知,两邻边和对角线的长短关系因两邻边的夹角不同而不 D.F增大、v减小 同,当两邻边长短不变,而夹角改变时,对角线的长短也将发 答案D 生改变,即合速度也将变化,选项A、B、D错误,C正确。 解析设绳子与竖直方向上的夹角为日,因为A做匀速直 2.(多选)关于运动的合成,下列说法正确的是( 线运动,在竖直方向上合力为零,有Fcos0=mg,因为日 A.两个直线运动的合运动,一定是直线运动 增大,则F增大。物体A沿绳子方向上的分速度 B.两个直线运动的合运动,可能是曲线运动 v=V物c0s0,因为0增大,则v减小,选项D正确。 C,两个互成角度的匀速直线运动的合运动,一定是匀速 5.雨滴正在以4m/s的速度竖直下落,忽然一阵风以3m/s 直线运动 的速度水平吹来,正在雨中撑伞行走的人,为使雨滴尽量 D.两个互成角度的匀加速直线运动的合运动,一定是匀 不落在身上,手中伞杆应与竖直方向所成夹角为( 加速直线运动 A.30° B.37° C.459 D.0° 答案BC 答案B 解析两个匀速直线运动的合成,就是其速度的合成,其 解析雨滴同时参与两个方向的分运动,一是竖直向下的 合速度是确定的,等于两个分速度的失量和,加速度为零, 匀速直线运动,二是沿水平方向的匀速直线运动,其合速 即合力为零,故合运动一定是匀速直线运动,选项C正 确:两个分运动的合加速度的方向与合速度的方向不一定 度方向与竖直方向的夹角为0,am0=”= 4,所以0= 在同一直线上,既有可能做曲线运动,也有可能做直线运 37°。为使雨滴尽量不落在身上,应使伞面与雨滴速度方 动,不是“一定”,而是“可能”,故选项A、D错误,B正确。 向垂直,伞杆与雨滴的速度方向平行,所以,伞杆与竖直方 3.(多选)跳伞表演是人们普遍喜欢的观赏性 向应成37°夹角,选项B正确。 体育项目,如图所示,当运动员从直升机由 6.在一次漂流探险中,探险者驾驶摩托艇想上岸休息,江岸 静止跳下后,在下落过程中不免会受到水平 是平直的,江水沿江向下流速为,摩托艇在静水中航速 风力的影响,下列说法正确的是() 为,探险者离岸最近点O的距离为d。如果探险者想在 A.风力越大,运动员下落时间越长,运动员 最短的时间内靠岸,则摩托艇登陆的地点离O的距离为 可完成更多的动作 多少? B.风力越大,运动员着地速度越大,有可能对运动员造成伤害 C.运动员下落时间与风力无关 答案 D.运动员着地速度与风力无关 解析如果探险者想在最短的时间 答案BC 内靠岸,摩托艇的船头应垂直于河 解析根据运动的独立性原理,水平方向吹来的风不会影 岸,即垂直于河岸,如图所示,则 响竖直方向的运动,选项A错误,C正确:根据速度的合 探险者运动的时间为=d ,那么摩 成,落地时速度v=√0,2十U,,风速越大,V,越大,则降 落伞落地时速度越大,选项B正确,D错误。 托艇登陆的地,点离O的距离为x=t= 课后·训练提升 合格考·基础巩固 的是( A.合运动的时间一定比每一个分运动的时间长 一、选择题(第1~4题为单选题,第5~7题为多选题) B.合运动的位移一定比每一个分运动的位移大 1在将一个合运动分解为两个分运动后,关于这个合运动 C.合运动的速度一定比每一个分运动的速度大 与它的两个分运动的物理量之间的关系,下列说法正确 D.合运动的加速度可能比每一个分运动的加速度都小
物 理 必修 第二册 配人教版 随堂训练 1.对于两个分运动的合运动,下列说法正确的是( ) A.合运动的速度大小等于两个分运动的速度大小之和 B.合运动的速度一定大于某一个分运动的速度 C.合运动的方向就是物体实际运动的方向 D.由两个分速度的大小就可以确定合速度的大小 答案 C 解析 根据平行四边形定则知,邻边表示两个分运动的速 度,合运动的速度的大小和方向可由对角线表示,由几何关 系知,两邻边和对角线的长短关系因两邻边的夹角不同而不 同,当两邻边长短不变,而夹角改变时,对角线的长短也将发 生改变,即合速度也将变化,选项A、B、D错误,C正确。 2.(多选)关于运动的合成,下列说法正确的是( ) A.两个直线运动的合运动,一定是直线运动 B.两个直线运动的合运动,可能是曲线运动 C.两个互成角度的匀速直线运动的合运动,一定是匀速 直线运动 D.两个互成角度的匀加速直线运动的合运动,一定是匀 加速直线运动 答案 BC 解析 两个匀速直线运动的合成,就是其速度的合成,其 合速度是确定的,等于两个分速度的矢量和,加速度为零, 即合力为零,故合运动一定是匀速直线运动,选项 C正 确;两个分运动的合加速度的方向与合速度的方向不一定 在同一直线上,既有可能做曲线运动,也有可能做直线运 动,不是“一定”,而是“可能”,故选项 A、D错误,B正确。 3.(多选)跳伞表演是人们普遍喜欢的观赏性 体育项目,如图所示,当运动员从直升机由 静止跳下后,在下落过程中不免会受到水平 风力的影响,下列说法正确的是( ) A.风力越大,运动员下落时间越长,运动员 可完成更多的动作 B.风力越大,运动员着地速度越大,有可能对运动员造成伤害 C.运动员下落时间与风力无关 D.运动员着地速度与风力无关 答案 BC 解析 根据运动的独立性原理,水平方向吹来的风不会影 响竖直方向的运动,选项 A 错误,C正确;根据速度的合 成,落地时速度v= vx 2+vy 2 ,风速越大,vx 越大,则降 落伞落地时速度越大,选项B正确,D错误。 4.如图所示,中间有孔的物块 A 套在光滑的 竖直杆上,通过滑轮用不可伸长的轻绳将 物体拉着匀速向上运动。则关于拉力 F 及拉力作用点的移动速度v,下列说法正确 的是( ) A.F 不变、v不变 B.F 增大、v不变 C.F 增大、v增大 D.F 增大、v减小 答案 D 解析 设绳子与竖直方向上的夹角为θ,因为 A做匀速直 线运动,在竖直方向上合力为零,有Fcosθ=mg,因为θ 增大,则 F 增 大。物 体 A 沿 绳 子 方 向 上 的 分 速 度 v=v物 cosθ,因为θ增大,则v减小,选项D正确。 5.雨滴正在以4m/s的速度竖直下落,忽然一阵风以3m/s 的速度水平吹来,正在雨中撑伞行走的人,为使雨滴尽量 不落在身上,手中伞杆应与竖直方向所成夹角为( ) A.30° B.37° C.45° D.0° 答案 B 解析 雨滴同时参与两个方向的分运动,一是竖直向下的 匀速直线运动,二是沿水平方向的匀速直线运动,其合速 度方向与竖直方向的夹角为θ,tanθ= vx vy = 3 4 ,所以θ= 37°。为使雨滴尽量不落在身上,应使伞面与雨滴速度方 向垂直,伞杆与雨滴的速度方向平行,所以,伞杆与竖直方 向应成37°夹角,选项B正确。 6.在一次漂流探险中,探险者驾驶摩托艇想上岸休息,江岸 是平直的,江水沿江向下流速为v,摩托艇在静水中航速 为u,探险者离岸最近点O 的距离为d。如果探险者想在 最短的时间内靠岸,则摩托艇登陆的地点离O 的距离为 多少? 答案 v u d 解析 如果探险者想在最短的时间 内靠岸,摩托艇的船头应垂直于河 岸,即u 垂直于河岸,如图所示,则 探险者运动的时间为t= d u ,那么摩 托艇登陆的地点离O 的距离为x=vt= v u d。 课后·训练提升 合格考 基础巩固 一、选择题(第1~4题为单选题,第5~7题为多选题) 1.在将一个合运动分解为两个分运动后,关于这个合运动 与它的两个分运动的物理量之间的关系,下列说法正确 的是( ) A.合运动的时间一定比每一个分运动的时间长 B.合运动的位移一定比每一个分运动的位移大 C.合运动的速度一定比每一个分运动的速度大 D.合运动的加速度可能比每一个分运动的加速度都小 12

第五章 抛体运动 答案D 运动,它们之间的关系如图所示。 解析分运动与合运动具有等时性,即时间相等,故选项 A错误:合运动的位移等于分运动的位移的失量和,由平 行四边形定则可知,合位移的大小可能比分位移大,可能 比分位移小,可能与分位移相等,故选项B错误:合速度 等于分速度的失量和,由平行四边形定则可知,合速度的 大小可能比分速度大,可能比分速度小,可能与分速度相 由几何关系可得u=选项D正璃。 等,故选项C错误:合加速度等于分加速度的失量和,由 5.雨滴由静止开始下落,遇到水平方向吹来的风,下列说法 平行四边形定则可知,合加速度的大小可能比分加速度 正确的是() 大,可能比分加速度小,可能与分加速度相等,故选项D A.风速越大,雨滴下落时间越长 正确。 B.风速越大,雨滴着地时速度越大 2.如图所示,竖直放置的两端封闭的玻B邻 D C,雨滴下落时间与风速无关 璃管中注满清水,内有一个红蜡块能 Q D.雨滴着地速度与风速无关 在水中以速度)匀速上浮。红蜡块 答案BC 从玻璃管的下端匀速上浮的同时,使 R 解析将雨滴的运动分解为水平方向和竖直方向的运动, 玻璃管由静止水平向右做匀加速运 两个分运动相互独立,雨滴下落时间与竖直高度有关,与 动,则红蜡块的轨迹可能是() 水平方向的风速无关,选项A错误,C正确。风速越大, A.直线P B.曲线Q 落地时,雨滴水平方向分速度越大,合速度也越大,选项B C.曲线R D.无法确定 正确,D错误。 答案B 6.如图所示,某同学在研究运动的 解析红蜡块在竖直方向上做匀速直线运动,在水平方向 合成时做了如下活动:用左手沿 上做匀加速直线运动,所受合力方向水平向右,合力与合 黑板推动刻度尺竖直向上运动, 速度不共线,红蜡块的轨迹应为曲线,选项A错误:由于 运动中保持刻度尺水平,同时,用 做曲线运动的物体所受合力应指向运动轨迹凹的一侧,选 右手沿刻度尺向右移动笔尖。若该同学左手的运动为匀 项B正确,C、D错误。 速运动,右手相对于刻度尺的运动为初速度为零的匀加速 3.如图所示,假如飞机起飞时以v三 运动,则关于笔尖的实际运动,下列说法正确的是() 300km/h的速度斜向上飞行,飞行 A.笔尖做匀速直线运动 方向与水平面的夹角为30°,则竖直园 <30 B.笔尖做匀变速直线运动 方向的分速度为( C,笔尖做匀变速曲线运动 A.wtan30° B.vcos30° D.笔尖的速度方向与水平方向夹角逐渐变小 C.150 km/h D.150√/3km/h 答案CD 答案C 解析由题意知,笔尖的初速度方向竖直向上,水平向右 解析将飞机的实际运动分解巴 的加速度恒定,故笔尖做匀变速曲线运动,选项A、B错 为水平方向的匀速运动和竖直 误,C正确:由于竖直方向速度大小恒定,水平方向速度大 方向的匀速运动,如图所示,由 小逐渐增大,故笔尖的速度方向与水平方向的夹角逐渐变 几何关系,可得v,=vsin30°= 小,选项D正确。 7.如图所示,在距河面高度h=20m的岸上有人用长绳拴 300km/h×2=150km/h,选项C正确,A,B,D错误。 住一条小船,开始时绳与水面的夹角为30°。人以恒定的 4.人用绳子通过定滑轮拉物体A,A穿 速率v=3m/s拉绳,使小船靠岸,sin53°=0.8,cos53°= 在光滑的竖直杆上,当以速度。匀 0.6,那么( 速地拉绳使物体A到达如图所示位 置时,绳与竖直杆的夹角为8,则物体 A实际运动的速度是( ) 30 时 A.vosin B.o C.vocos D. Vo sin 0 cos 0 A.5s时绳与水面的夹角为60° B.5s时小船前进了15m 答案D C.5s时小船的速率为5m/s 解析由运动的合成与分解可知,物体A参与两个分运 D.5s时小船到岸边的距离为15m 动,一个是沿着与它相连接的绳子的运动,另一个是垂直 答案CD 于绳子斜向上的运动。而物体A的实际运动轨迹是沿着 h 竖直杆向上的,这一轨迹所对应的运动就是物体A的合 解析设开始时小船距岸边为,则1= tan30°= 13
第五章 抛体运动 答案 D 解析 分运动与合运动具有等时性,即时间相等,故选项 A错误;合运动的位移等于分运动的位移的矢量和,由平 行四边形定则可知,合位移的大小可能比分位移大,可能 比分位移小,可能与分位移相等,故选项 B错误;合速度 等于分速度的矢量和,由平行四边形定则可知,合速度的 大小可能比分速度大,可能比分速度小,可能与分速度相 等,故选项 C错误;合加速度等于分加速度的矢量和,由 平行四边形定则可知,合加速度的大小可能比分加速度 大,可能比分加速度小,可能与分加速度相等,故选项 D 正确。 2.如图所示,竖直放置的两端封闭的玻 璃管中注满清水,内有一个红蜡块能 在水中以速度v 匀速上浮。红蜡块 从玻璃管的下端匀速上浮的同时,使 玻璃管由静止水平向右做匀加速运 动,则红蜡块的轨迹可能是( ) A.直线P B.曲线Q C.曲线R D.无法确定 答案 B 解析 红蜡块在竖直方向上做匀速直线运动,在水平方向 上做匀加速直线运动,所受合力方向水平向右,合力与合 速度不共线,红蜡块的轨迹应为曲线,选项 A 错误;由于 做曲线运动的物体所受合力应指向运动轨迹凹的一侧,选 项B正确,C、D错误。 3.如图所示,假如飞机起飞时以v= 300km/h的速度斜向上飞行,飞行 方向与水平面的夹角为30°,则竖直 方向的分速度为( ) A.vtan30° B.vcos30° C.150km/h D.1503km/h 答案 C 解析 将飞机的实际运动分解 为水平方向的匀速运动和竖直 方向的匀速运动,如图所示,由 几何关系,可得vy=vsin30°= 300km/h× 1 2 =150km/h,选项C正确,A、B、D错误。 4.人用绳子通过定滑轮拉物体 A,A穿 在光滑的竖直杆上,当以速度v0 匀 速地拉绳使物体 A 到达如图所示位 置时,绳与竖直杆的夹角为θ,则物体 A实际运动的速度是( ) A.v0sinθ B. v0 sinθ C.v0cosθ D. v0 cosθ 答案 D 解析 由运动的合成与分解可知,物体 A 参与两个分运 动,一个是沿着与它相连接的绳子的运动,另一个是垂直 于绳子斜向上的运动。而物体 A的实际运动轨迹是沿着 竖直杆向上的,这一轨迹所对应的运动就是物体 A 的合 运动,它们之间的关系如图所示。 由几何关系可得v= v0 cosθ ,选项D正确。 5.雨滴由静止开始下落,遇到水平方向吹来的风,下列说法 正确的是( ) A.风速越大,雨滴下落时间越长 B.风速越大,雨滴着地时速度越大 C.雨滴下落时间与风速无关 D.雨滴着地速度与风速无关 答案 BC 解析 将雨滴的运动分解为水平方向和竖直方向的运动, 两个分运动相互独立,雨滴下落时间与竖直高度有关,与 水平方向的风速无关,选项 A 错误,C正确。风速越大, 落地时,雨滴水平方向分速度越大,合速度也越大,选项B 正确,D错误。 6.如图所示,某同学在研究运动的 合成时做了如下活动:用左手沿 黑板推动刻度尺竖直向上运动, 运动中保持刻度尺水平,同时,用 右手沿刻度尺向右移动笔尖。若该同学左手的运动为匀 速运动,右手相对于刻度尺的运动为初速度为零的匀加速 运动,则关于笔尖的实际运动,下列说法正确的是( ) A.笔尖做匀速直线运动 B.笔尖做匀变速直线运动 C.笔尖做匀变速曲线运动 D.笔尖的速度方向与水平方向夹角逐渐变小 答案 CD 解析 由题意知,笔尖的初速度方向竖直向上,水平向右 的加速度恒定,故笔尖做匀变速曲线运动,选项 A、B错 误,C正确;由于竖直方向速度大小恒定,水平方向速度大 小逐渐增大,故笔尖的速度方向与水平方向的夹角逐渐变 小,选项D正确。 7.如图所示,在距河面高度h=20m 的岸上有人用长绳拴 住一条小船,开始时绳与水面的夹角为30°。人以恒定的 速率v=3m/s拉绳,使小船靠岸,sin53°=0.8,cos53°= 0.6,那么( ) A.5s时绳与水面的夹角为60° B.5s时小船前进了15m C.5s时小船的速率为5m/s D.5s时小船到岸边的距离为15m 答案 CD 解析 设 开 始 时 小 船 距 岸 边 为 l,则 l= h tan30° = 13

物理 必修 第二册 配人教版 205m,5s时人拉绳端移动位移为x=t=3X5m= 2.某校在教室安装了可以左 15m,设5s时绳与水面的夹角为0,由几何关系得sim0= 右滑动的黑板,如图所示。 2h-7=0.8,解得0=53,选项A错误:设5s时小船前 h 一位老师用粉笔在其中某 块可移动的黑板上画直 h 线,若粉笔相对于黑板从静止开始向上匀加速滑动,同时 进了x,由an0=-7,解得x=19.64m,选项B错 黑板以某一速度水平向左匀速运动,则粉笔画出的轨迹可 误;由v“cos0=v,可得5s时小船的速率为v#=5m/s, 能为下列中的( 选项C正确:5s时小船到岸边的距离为1一工=, tan 15m,选项D正确。 二、计算题 8.某直升机空投物资时,可以停留在空中不动,设投出的物 答案C 资离开飞机后由于降落伞的作用在空中能匀速下落,无风 解析黑板以某一速度水平向左匀速运动,同时粉笔相对 时落地速度为5m/s。若飞机停留在离地面100m高处 于黑板从静止开始匀加速向上滑动,所以粉笔的合初速度 空投物资,由于风的作用,使降落伞和物资以1m/s的速 向右,合加速度向上,所以轨迹是曲线并且合力指向曲线 度匀速水平向北运动,求: 凹侧,故选项C正确,A、BD错误。 (1)物资在空中运动的时间: 3.固定在竖直平面内的半圆形刚性铁 (2)物资落地时速度的大小: 环,半径为R,铁环上穿着小球,铁环 30 160 (3)物资在下落过程中水平方向移动的距离。 圆心O的正上方固定一个小定滑 答案(1)20s(2)√26m/s(3)20m 轮。用一条不可伸长的细绳,通过 解析如图所示,物资的实际运动可以看 定滑轮以一定速度拉着小球从A点 60210 作是竖直方向的匀速直线运动和水平方 开始沿铁环运动,某时刻角度关系 向的匀速直线运动两个分运动的合运动。 如图所示,若绳末端速度为,则小球此时的速度为( ) (1)分运动与合运动具有等时性,故 物资实际运动的时间与竖直方向分运动的时间相等。 A33 3 v B.√2u C.3v D.2v 所以1=力=100 答案A vy 5 =20s。 解析小球的速度沿圆孤的切线方向,将小球的速度分解 (2)物资落地时,=5m/s,v,=1m/s,由平行四边 为沿绳子方向和垂直绳子方向的分量,沿绳子方向的速度 形定则得 v=√0.2+u,2=√12+5m/s=√/26m/s。 为v,则tc0s30°=u,解得=2 ,故选项A正确。 3 (3)物资在下落过程中水平方向移动的距离为 x=vt=1X20m=20m。 30° 60 等级考:拓展提高 选择题(第14题为单选题,第5~7题为多选题) 1如图所示,帆板在海面上以速 度朝正西方向运动,帆船以 4.如图所示,小船以大小为、方 向与上游河岸成日角的速度(在 -一”水流 速度v朝正北方向航行,以帆 上游 板为参考系( 静水中的速度)从A处过河,经 A.帆船朝正东方向航行,速度 过t时间正好到达正对岸的B处。现要使小船在更短的 大小为 时间内过河并且也正好到达正对岸B处,在水流速度不 B.帆船朝正西方向航行,速度 变的情况下,可采取的方法是( 大小为 A.只增大1大小,不改变0角 B.只增大0角,不改变1大小 C.帆船朝南偏东45方向航行,速度大小为√2u C.在增大v1的同时,适当减小0角 D.帆船朝北偏东45°方向航行,速度大小为√2v D.在增大1的同时,适当增大0角 答案D 答案D 解析以帆板为参考系,在东西方向上,帆船相对于帆板 解析小船过河的时间取决于垂直河岸方向的速度,即 向东运动:在南北方向上,帆船相对于帆板向北运动:二者 v1sin0,要使小船到达B点,且时间变短,则v1sin0应增 速度大小相等,因此帆船朝北偏东45°方向航行,速度大小 大,同时小船在沿河岸方向的速度仍应为零,即1c0s日的 为√02十u=反u,选项D正确。 值不变,因此需要增大1,同时增大0角,故选项D正确。 14
物 理 必修 第二册 配人教版 203 m,5s时人拉绳端移动位移为x=vt=3×5m= 15m,设5s时绳与水面的夹角为θ,由几何关系得sinθ= h 2h-x =0.8,解得θ=53°,选项 A 错误;设5s时小船前 进了x',由tanθ= h l-x' ,解得x'=19.64m,选项 B错 误;由v船cosθ=v,可得5s时小船的速率为v船 =5m/s, 选项C正确;5s时小船到岸边的距离为l-x'= h tanθ = 15m,选项D正确。 二、计算题 8.某直升机空投物资时,可以停留在空中不动,设投出的物 资离开飞机后由于降落伞的作用在空中能匀速下落,无风 时落地速度为5m/s。若飞机停留在离地面100m 高处 空投物资,由于风的作用,使降落伞和物资以1m/s的速 度匀速水平向北运动,求: (1)物资在空中运动的时间; (2)物资落地时速度的大小; (3)物资在下落过程中水平方向移动的距离。 答案 (1)20s (2) 26 m/s (3)20m 解析 如图所示,物资的实际运动可以看 作是竖直方向的匀速直线运动和水平方 向的匀速直线运动两个分运动的合运动。 (1)分运动与合运动具有等时性,故 物资实际运动的时间与竖直方向分运动的时间相等。 所以t= h vy = 100 5 s=20s。 (2)物资落地时vy=5m/s,vx=1m/s,由平行四边 形定则得 v= vx 2+vy 2 = 12+52 m/s= 26 m/s。 (3)物资在下落过程中水平方向移动的距离为 x=vxt=1×20m=20m。 等级考 拓展提高 选择题(第1~4题为单选题,第5~7题为多选题) 1.如图所示,帆板在海面上以速 度v 朝正西方向运动,帆船以 速度v 朝正北方向航行,以帆 板为参考系( ) A.帆船朝正东方向航行,速度 大小为v B.帆船朝正西方向航行,速度 大小为v C.帆船朝南偏东45°方向航行,速度大小为 2v D.帆船朝北偏东45°方向航行,速度大小为 2v 答案 D 解析 以帆板为参考系,在东西方向上,帆船相对于帆板 向东运动;在南北方向上,帆船相对于帆板向北运动;二者 速度大小相等,因此帆船朝北偏东45°方向航行,速度大小 为 v2+v2 = 2v,选项D正确。 2.某校在教室安装了可以左 右滑动的黑板,如图所示。 一位老师用粉笔在其中某 块可 移 动 的 黑 板 上 画 直 线,若粉笔相对于黑板从静止开始向上匀加速滑动,同时 黑板以某一速度水平向左匀速运动,则粉笔画出的轨迹可 能为下列中的( ) 答案 C 解析 黑板以某一速度水平向左匀速运动,同时粉笔相对 于黑板从静止开始匀加速向上滑动,所以粉笔的合初速度 向右,合加速度向上,所以轨迹是曲线并且合力指向曲线 凹侧,故选项C正确,A、B、D错误。 3.固定在竖直平面内的半圆形刚性铁 环,半径为R,铁环上穿着小球,铁环 圆心O 的正上方固定一个小定滑 轮。用一条不可伸长的细绳,通过 定滑轮以一定速度拉着小球从A 点 开始沿铁环运动,某时刻角度关系 如图所示,若绳末端速度为v,则小球此时的速度为( ) A. 23 3 v B.2v C.3v D.2v 答案 A 解析 小球的速度沿圆弧的切线方向,将小球的速度分解 为沿绳子方向和垂直绳子方向的分量,沿绳子方向的速度 为v,则v'cos30°=v,解得v'= 23 3 v,故选项 A正确。 4.如图所示,小船以大小为v1、方 向与上游河岸成θ角的速度(在 静水中的速度)从A 处过河,经 过t时间正好到达正对岸的B 处。现要使小船在更短的 时间内过河并且也正好到达正对岸B 处,在水流速度不 变的情况下,可采取的方法是( ) A.只增大v1 大小,不改变θ角 B.只增大θ角,不改变v1 大小 C.在增大v1 的同时,适当减小θ角 D.在增大v1 的同时,适当增大θ角 答案 D 解析 小船过河的时间取决于垂直河岸方向的速度,即 v1sinθ,要使小船到达B 点,且时间变短,则v1sinθ应增 大,同时小船在沿河岸方向的速度仍应为零,即v1cosθ的 值不变,因此需要增大v1,同时增大θ角,故选项D正确。 14

第五章 抛体运动 5.如图所示,在灭火抢险的过程中, 7.一小船在静水中的速度为3m/s,它在一条河宽为150m、 消防队员有时要借助消防车上的 水流速度为4m/s的河流中渡河,则该小船() 梯子爬到高处进行救人或灭火作 A.不能到达正对岸 业。为了节省救援时间,人沿梯子 B.渡河的时间可能少于50s 匀加速向上运动的同时消防车匀 C.以最短时间渡河时,它沿水流方向的位移大小为200m 速后退,从地面上看,下列说法正确的是( D.以最短位移渡河时,位移大小为150m A.消防队员做匀加速直线运动 答案AC B.消防队员做匀变速曲线运动 解析因为小船在静水中的速度小于水流速度,所以小船 C.消防队员做变加速曲线运动 不能到达正对岸,选项A正确:当船头与河岸垂直时渡河 D.消防队员水平方向的速度变大 答案BD 时间最短,最短时间1==50s,故渡河时间不能少于 U越 解析根据运动的合成知合速度的方向与合加速度的方 50$,选项B错误:以最短时间渡河时,沿水流方向位移 向不在同一条直线上,但其加速度的方向和大小不变,所 x=v水t=200m,选项C正确;当v与实际运动方向垂 以消防队员做匀变速曲线运动,选项A、C错误,B正确: 直时渡河位移最短,设此时船头与河岸的夹角为日,则 将消防队员的运动分解为水平方向和竖直方向,知水平方 cos 0= 向上的合速度为匀速后退的速度和沿梯子方向的速度在 ,故淀河位移:=心=200m选预D辑民。 水平方向上的分速度的合成,而沿梯子方向的速度在水平 挑战·创新 方向上的分速度在变大,选项D正确。 6.如图所示,在不计滑轮摩擦和绳子 船在静水中的速度与时间的关系如图甲所示,河水的流速 质量的条件下,小车匀速地从B 与船离河岸的距离d的变化关系如图乙所示,求: A 点运动到M点,再运动到N点的 40m·s-) 水/ms-) 过程中,关于物体A的运动和受 力情况,下列说法正确的是( A物体A也做匀速直线运动 150 300 d/m B.物体A的速度可能为零 C.绳的拉力总是等于A的重力 (1)小船渡河的最短时间: D.绳的拉力总是大于A的重力 (2)小船以最短时间渡河的位移。 答案BD 答案(1)100s(2)100√13m 解析设和小车连接的绳子与水平面的夹角为日,小车的 解析(1)由题图可知,v“=3m/s,河宽d=300m,船头 速度为,则这个速度分解为沿绳方向向上和垂直绳方向 正对对岸则渡河时间最短, 向下的速度,解得沿绳方向的速度为ucos0。随着小车匀 速向左运动,显然日先增大后减小,所以绳方向的分速度 d=100s0 故t咖一 先减小后增大。又知物体A的速度与绳方向分速度大小 (2)当小船船头正对对岸行驶时,*先随时间线性增 一样,则在小车从右向左匀速行驶的过程中物体A先向 大,后线性减小, 下做减速运动,然后向上做加速运动,加速度始终向上。 河水最大流速为V水m=4m/S。 当小车到达M点时,绳子的速度为零,则物体A的速度 垂直河岸的分位移x1=d=300m 也为零。由牛顿第二定律得F一mg=ma,即F=mg十 ma,因此,绳的拉力总大于物体A的重力,选项A、C错 沿河岸方向的分位移x:=2×(7.艺)=20m 误,B、D正确。 总位移x=100√13m。 3 实验:探究平抛运动的特点 实验探究·方案梳理 实验目的 向的分运动的特点。 3.掌握描迹法、频闪照相法等探究实验的常用方法。 1.学会用实验的方法描绘平抛运动的轨迹。 2.会根据实验结果分析平抛运动在水平方向和竖直方 15
第五章 抛体运动 5.如图所示,在灭火抢险的过程中, 消防队员有时要借助消防车上的 梯子爬到高处进行救人或灭火作 业。为了节省救援时间,人沿梯子 匀加速向上运动的同时消防车匀 速后退,从地面上看,下列说法正确的是( ) A.消防队员做匀加速直线运动 B.消防队员做匀变速曲线运动 C.消防队员做变加速曲线运动 D.消防队员水平方向的速度变大 答案 BD 解析 根据运动的合成知合速度的方向与合加速度的方 向不在同一条直线上,但其加速度的方向和大小不变,所 以消防队员做匀变速曲线运动,选项 A、C错误,B正确; 将消防队员的运动分解为水平方向和竖直方向,知水平方 向上的合速度为匀速后退的速度和沿梯子方向的速度在 水平方向上的分速度的合成,而沿梯子方向的速度在水平 方向上的分速度在变大,选项D正确。 6.如图所示,在不计滑轮摩擦和绳子 质量的条件下,小车匀速地从 B 点运动到M 点,再运动到 N 点的 过程中,关于物体 A 的运动和受 力情况,下列说法正确的是( ) A.物体 A也做匀速直线运动 B.物体 A的速度可能为零 C.绳的拉力总是等于 A的重力 D.绳的拉力总是大于 A的重力 答案 BD 解析 设和小车连接的绳子与水平面的夹角为θ,小车的 速度为v,则这个速度分解为沿绳方向向上和垂直绳方向 向下的速度,解得沿绳方向的速度为vcosθ。随着小车匀 速向左运动,显然θ先增大后减小,所以绳方向的分速度 先减小后增大。又知物体 A的速度与绳方向分速度大小 一样,则在小车从右向左匀速行驶的过程中物体 A 先向 下做减速运动,然后向上做加速运动,加速度始终向上。 当小车到达M 点时,绳子的速度为零,则物体 A 的速度 也为零。由牛顿第二定律得F-mg=ma,即F=mg+ ma,因此,绳的拉力总大于物体 A 的重力,选项 A、C错 误,B、D正确。 7.一小船在静水中的速度为3m/s,它在一条河宽为150m、 水流速度为4m/s的河流中渡河,则该小船( ) A.不能到达正对岸 B.渡河的时间可能少于50s C.以最短时间渡河时,它沿水流方向的位移大小为200m D.以最短位移渡河时,位移大小为150m 答案 AC 解析 因为小船在静水中的速度小于水流速度,所以小船 不能到达正对岸,选项 A正确;当船头与河岸垂直时渡河 时间最短,最短时间t= d v船 =50s,故渡河时间不能少于 50s,选项 B错误;以最短时间渡河时,沿水流方向位移 x=v水t=200m,选项C正确;当v船 与实际运动方向垂 直时渡河位移最短,设此时船头与河岸的夹角为θ,则 cosθ= 3 4 ,故渡河位移s= d cosθ =200m,选项D错误。 挑战 创新 船在静水中的速度与时间的关系如图甲所示,河水的流速 与船离河岸的距离d 的变化关系如图乙所示,求: (1)小船渡河的最短时间; (2)小船以最短时间渡河的位移。 答案 (1)100s (2)100 13 m 解析 (1)由题图可知,v船 =3m/s,河宽d=300m,船头 正对对岸则渡河时间最短, 故tmin= d v船 =100s。 (2)当小船船头正对对岸行驶时,v水 先随时间线性增 大,后线性减小, 河水最大流速为v水max=4m/s。 垂直河岸的分位移x1=d=300m 沿河岸方向的分位移x2=2× v水max 2 · tmin 2 =200m 总位移x=100 13 m。 3 实验:探究平抛运动的特点 实验探究·方案梳理 实验目的 1.学会用实验的方法描绘平抛运动的轨迹。 2.会根据实验结果分析平抛运动在水平方向和竖直方 向的分运动的特点。 3.掌握描迹法、频闪照相法等探究实验的常用方法。 15