图示电路共有三个电 流,因此有三条支路, 分别由ab、acb、 adb构成。 acb、adb两条支路 中含有电源,称为有源 支路;ab支路不含电 图示电路共有两个结点a和b 源,称为无源支路 对图示结点,其流入该结点的电流之和应该等于由该结点 流出的电流之和,即: I3=I1+I2
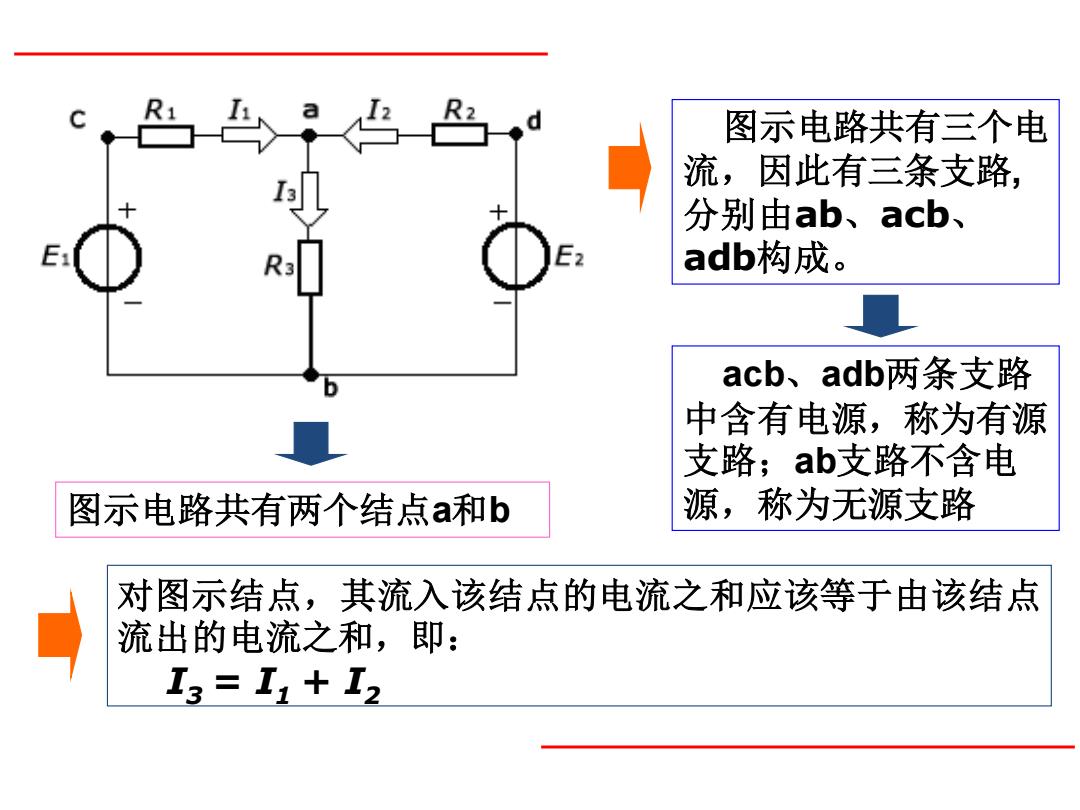
图示电路共有三个电 流,因此有三条支路, 分别由ab、acb、 adb构成。 图示电路共有两个结点a和b acb、adb两条支路 中含有电源,称为有源 支路;ab支路不含电 源,称为无源支路 对图示结点,其流入该结点的电流之和应该等于由该结点 流出的电流之和,即: I3 = I1 + I2
基尔霍夫电流定律通 常应用于结点,但也可 以应用于包围部分电路 的任一假设的闭合面 在图示电路中,有: IA Ie +Ic =0 可见,任一瞬时,通过任一闭 (请注意IA、IB、Ic 合面的电流的代数和恒等于0 均为流入电流) 可通过【例1.3.2】来理解
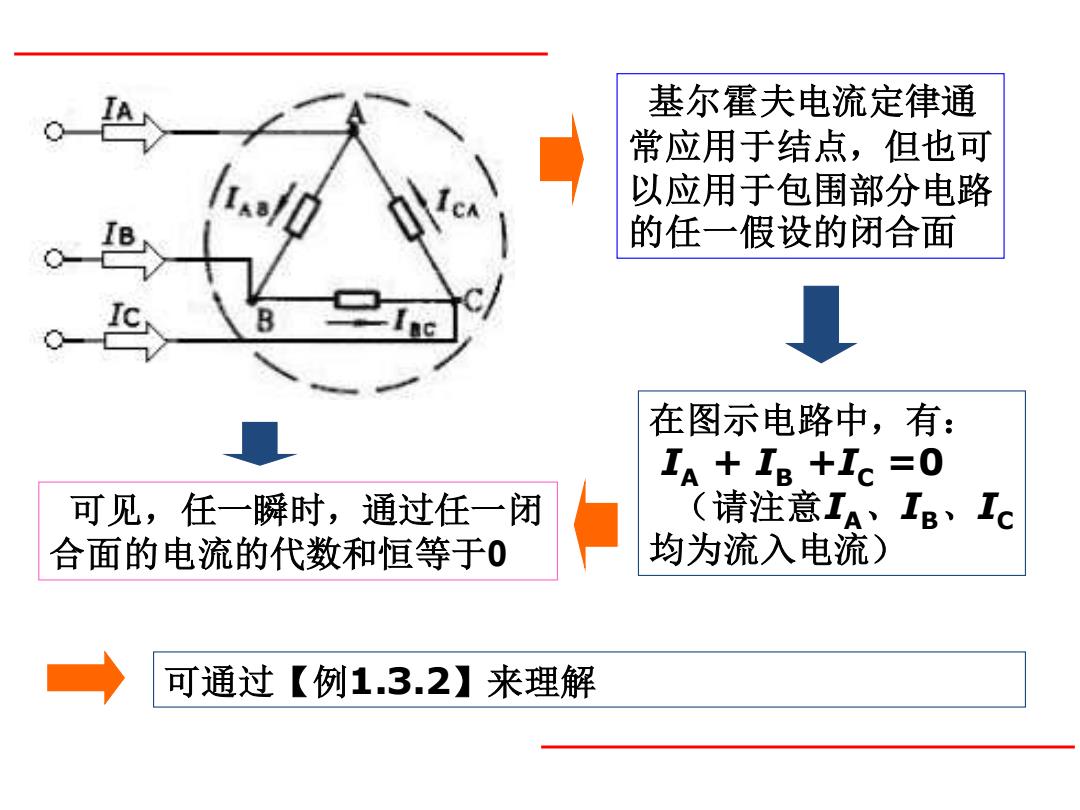
基尔霍夫电流定律通 常应用于结点,但也可 以应用于包围部分电路 的任一假设的闭合面 可见,任一瞬时,通过任一闭 合面的电流的代数和恒等于0 在图示电路中,有: IA + IB +IC =0 (请注意IA、IB、IC 均为流入电流) 可通过【例1.3.2】来理解

基尔霍夫电流定律的另外两种表 述方式 ·流入一个节点的电流代数和为零 ·流出一个节点的电流代数和为零
基尔霍夫电流定律的另外两种表 述方式 • 流入一个节点的电流代数和为零 • 流出一个节点的电流代数和为零

Node a Node b Node c i3 i6 (a) (b) (c) Node a:i+i2-i3 =0 Node a:-i1-i2+i3 =0 Node a:i+i2=i3 Node b:i3-i4=0 Node b:-i3+i4=0 Node b:i3 =i4 Node c:is+i6+i7=0 Node c:-is-i6-i7=0 Node c:is +i6+i7=0

练习 ·用KCL求解未知电流 3A 3A 3A 2A ia 4A (a) (b) (c)
练习 • 用KCL求解未知电流