
概率解释 ● 设预测结果0Tx(@与真实结果y(之间误差为e(@,即y)=0Tx(⊙+e) ●通常误差满足平均值为0的高斯分布,即正态分布。那么在一个样本 片x的概率套度公式为p00O:6)品exp(-093 22 ● 模型在全部样本上预测的最大似然估计为 wT2ap(-og 2G2 o=60=ma()-》,egx9 22 从而,需要∑10y0-07x@)最小 哈尔滨工业大学计算机学院刘远超
概率解释 l 设预测结果�&�(.) 与真实结果 �(.) 之间误差为�(.) ,即 �(.) = �& �(.) +�(.) l 通常误差满足平均值为0的高斯分布,即正态分布。那么在一个样本� 上�和�的概率密度公式为� � . � . ; � = ! "01 exp(− (2(&)',(+(&))# "1# ) l 模型在全部样本上预测的最大似然估计为 � � = -,-' + 1 2�� exp(− (�(,) −�& �(,) )* 2�* ) � � = ��� � = −��� 2�� −8,-' + (�(,) −�& �(,) )* 2�* 从而,需要 ! " ∑.3! $ (�(.) −�& �(.) )"最小 哈尔滨工业大学计算机学院 刘远超

求解参数 ●接下来,就是求解使得Σ沿10y@-日Tx⊙)最小的参数0。 ●解法有: ■矩阵解法。scikit--learn中的LinearRegression类使用的是矩阵解法( 有时也称为最小二乘法)。可以解出线性回归系数日。 ■梯度下降法。梯度下降(Gradient descent)是利用一阶的梯度信 息找到函数局部最优解的一种方法。 哈尔滨工业大学计算机学院刘远超
求解参数 l 接下来,就是求解使得 ! " ∑.3! $ (�(.) −�& �(.) )"最小的参数�。 l 解法有: n 矩阵解法。scikit-learn中的LinearRegression类使用的是矩阵解法( 有时也称为最小二乘法)。可以解出线性回归系数θ。 n 梯度下降法。 梯度下降(Gradient descent )是利用一阶的梯度信 息找到函数局部最优解的一种方法。 哈尔滨工业大学计算机学院 刘远超

参数的矩阵解法 例如,设Y=B+B1X:+e,即为线性关系→e=Y-阝o-B1X 0=∑12=∑-02=∑-瓦-x02 通过使Q最小,即可确定Fo,B1。 根据数学知识我们知道,函数的极值点为偏导为0的点,即 器=22票G-瓦-Ax-1)=0 =221(出-。-BX)(-X)=0 ∂B1 n∑XY-∑X:∑Yi →B0= n∑X:2-(EX)2 B= ∑x:2∑Y1-ZX:∑XY1 n∑X:2-(EX)2 哈尔滨工业大学计算机学院刘远超
参数的矩阵解法 例如,设�. = � G( + � G!�. + �.,即为线性关系⇒ �. = �. − � G( − � G!�. � = K�3� � �� � = K�3� � (�� − � G�)� = K�3� � (�� − � G� − � G���)� 通过使� 最小,即可确定� G�,� G�。 根据数学知识我们知道,函数的极值点为偏导为0的点,即 P 9: 9) ;) = 2 ∑.3! $ �. − � G( − � G!�. −1 = 0 9: 9) ;" = 2 ∑.3! $ �. − � G( − � G!�. −�. = 0 ⇒ �( = � ∑ �.�. − ∑ �. ∑ �. � ∑ �. " − (∑ �.)" �! = ∑ =& # ∑ >&'∑ =& ∑ =&>& # ∑ =& #'(∑ =&)# 哈尔滨工业大学计算机学院 刘远超
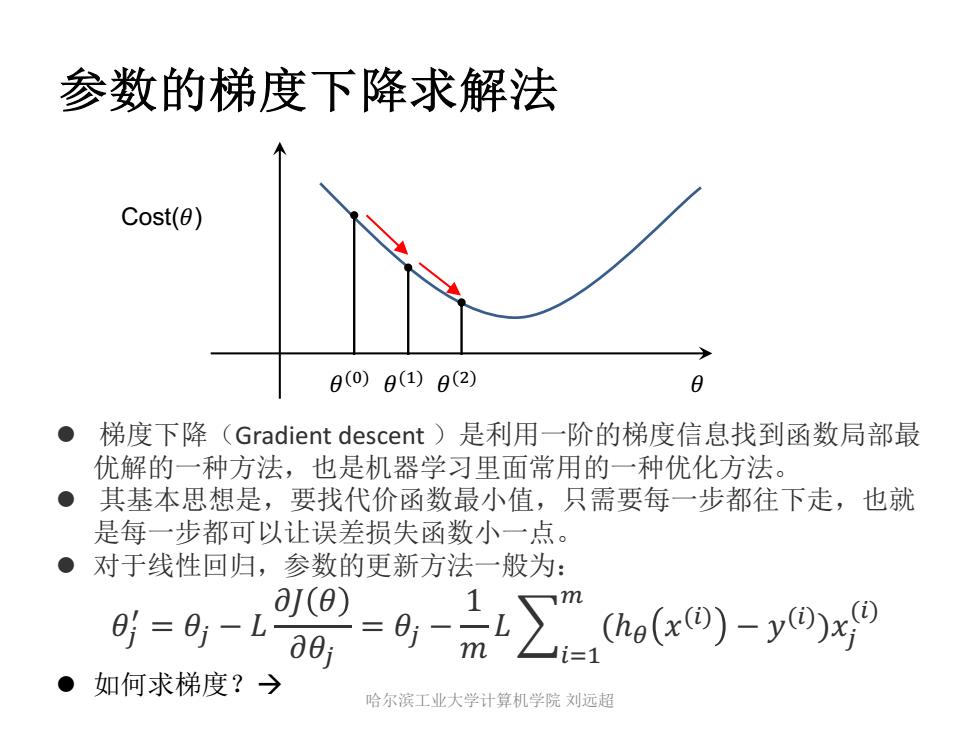
参数的梯度下降求解法 Cost(0) 0(0)0(1)0(2) 0 ●梯度下降(Gradient descent)是利用一阶的梯度信息找到函数局部最 优解的一种方法,也是机器学习里面常用的一种优化方法。 ● 其基本思想是,要找代价函数最小值,只需要每一步都往下走,也就 是每一步都可以让误差损失函数小一点。 对于线性回归,参数的更新方法一般为: =-点a.a-yog9 95=6-La8 如何求梯度?> 哈尔滨工业大学计算机学院刘远超
参数的梯度下降求解法 l 梯度下降(Gradient descent )是利用一阶的梯度信息找到函数局部最 优解的一种方法,也是机器学习里面常用的一种优化方法。 l 其基本思想是,要找代价函数最小值,只需要每一步都往下走,也就 是每一步都可以让误差损失函数小一点。 l 对于线性回归,参数的更新方法一般为: �0 1 = �0 − � �� � ��0 = �0 − 1 � �8,-' + (ℎ% �(,) − �(,) )�0 (,) l 如何求梯度?à Cost(�) �(#) �(%) �(&) � 哈尔滨工业大学计算机学院 刘远超