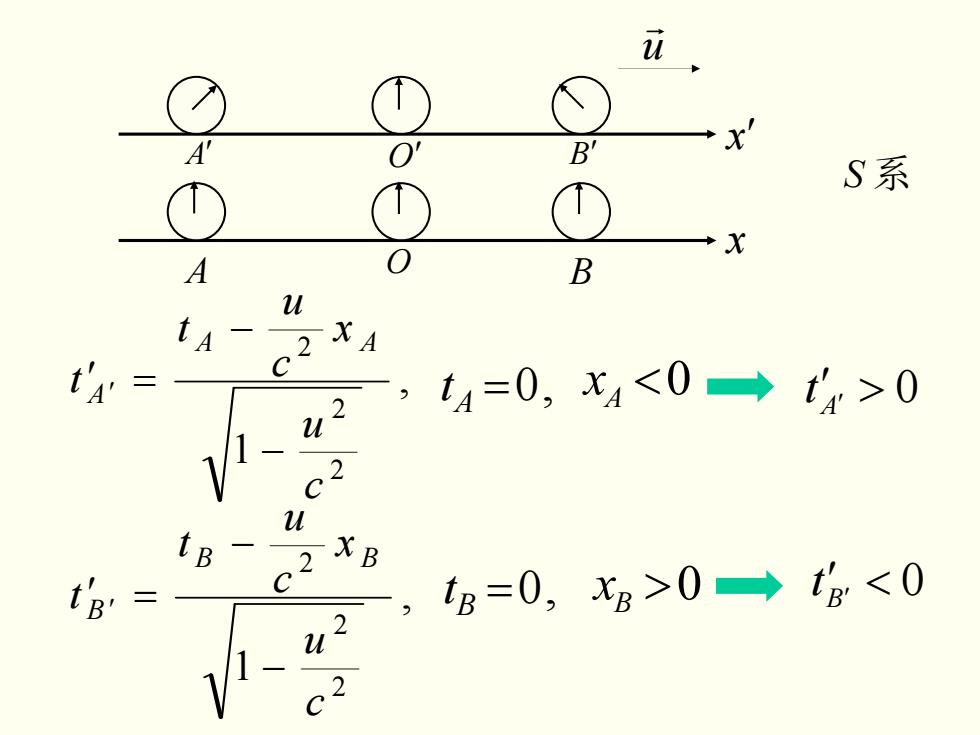
O' B 比 S系 X B u 、XA 2,=0,x<0→t>0 1 2 u c ,tB=0,xg>0→tg<0 u
A O B A′ O′ B′ x x ′ u r , 1 2 2 2 c u x c u t t A A A − − ′ ′ = , 1 2 2 2 c u x c u t t B B B − − ′ ′ = ′ ′ > 0 A =0, t At <0 Ax ′ ′ < 0 Bt =0, Bt >0 Bx S 系
A 0' B 比 -u S系 A 0 B -x t+ u XA tr=0,x4<0→t4<0 2 c3 u t8+ XB ,tg=0,xg>0→tg>0
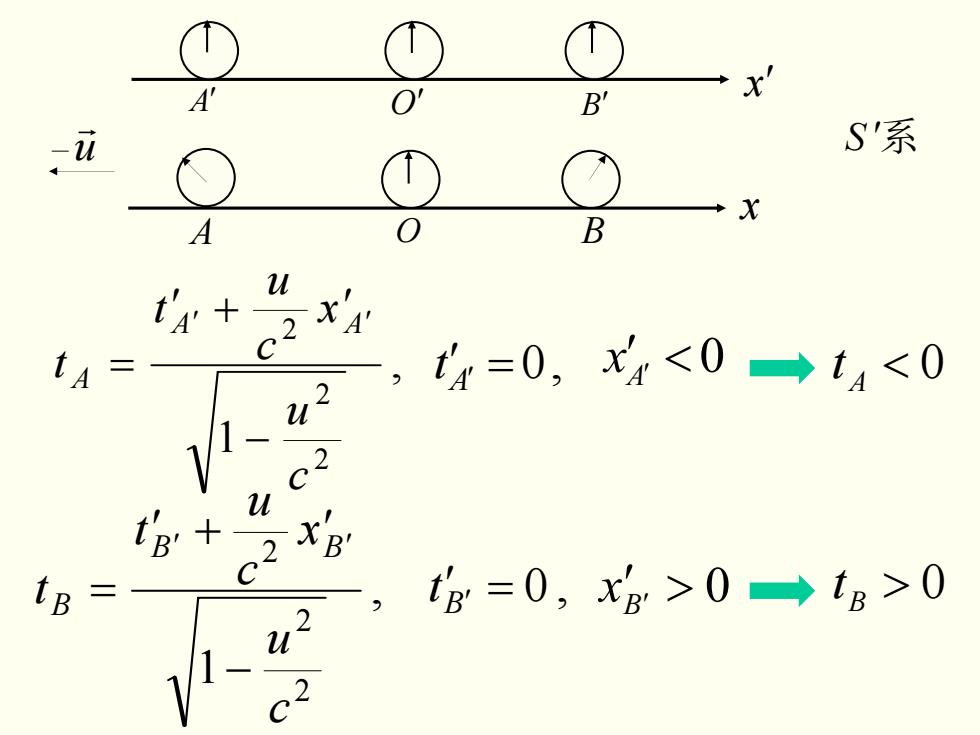
, 1 2 2 2 c u x c u t t A A A − ′ + ′ = ′ ′ , 1 2 2 2 c u x c u t t B B B − ′ + ′ = ′ ′ < 0 A ′ = , 0 t A′ t x ′ A′ < 0 ′ ′ = , 0 B t > 0 > 0 B ′ t x B′ A O B A′ O′ B′ x x′ u r S ′系

二、运动时钟的变慢 S系 P(xi,t) P(x2,2) xf =x, S系P(x,t) P2(x2,t2) t2-t1= 红总 u 2>1 →t2-t>t)-t
二、运动时钟的变慢 S ′系 ),( 111 ′ txP ′ ),( 222 ′ txP ′ S 系 ),( 111 txP ),( 222 txP ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ′ − ′ + ′ − ′ − =− )()( 1 1 12 2 12 2 2 12 xx c u tt c u tt 21′ = xx ′ 1 1 1 2 2 > − c u 1212 − > ′ − tttt ′ 2 2 12 1 c u tt − ′ − ′ =

某物体内部相继发生的两个事件P S系 P(xt) P2(xp:t2) △t'=t)-t S系 P(x1,41) P2(x2,t2) △t=t2-t1 △t △t= u 随某物体 (S系)一起运动的时钟所指示的时间 △T △t= 该物体的固有时△( △T=△t' △t>△t 运动物体上发生的自然过程比起静止物体的同样 过程延缓了 ◆运动时钟的延缓
某物体内部相继发生的两个事件 P1 P2 S ′系 ),( 11 ′ p txP ′ ),( 2 2 ′ p txP ′ 12 Δ ′ = ′ − ttt ′ S 系 ),( 111 txP ),( 222 txP 12 Δ = − ttt 2 2 1 c u t t − Δ ′ =Δ 随某物体 一起运动的时钟所指示的时间 ( ) S ′系 该物体的固有时 Δ τ 2 Δ τ = Δ t′ 2 1 c u t − Δ =Δ τ Δ t Δ> τ 运动物体上发生的自然过程比起静止物体的同样 过程延缓了 运动时钟的延缓
物体一S'系内的一个时钟 O 两个事件:t △t=t3-t好 时钟O'与时钟O相遇时 t1=t=0 时钟O'与时钟B相遇时 时钟O'一·t2 时钟B→t2 △t=t2-t1 △t>△t S系上的观察者认为运动时钟走得比静止时钟慢一些 ◆运动时钟的变慢!
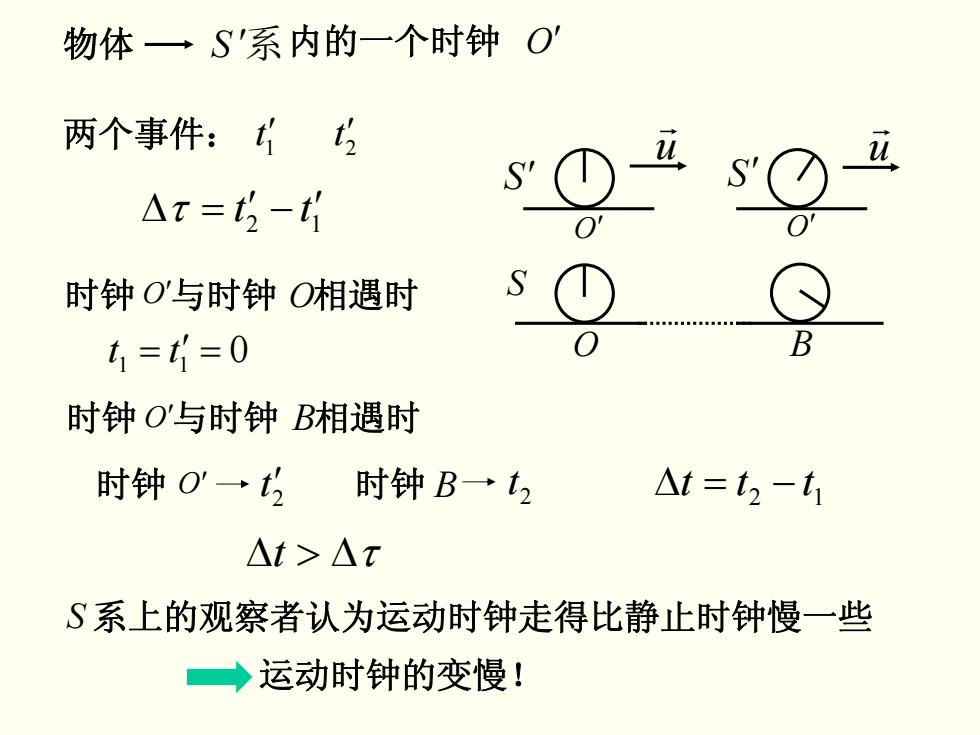
两个事件: 21′ tt ′ 12 Δτ = ′ − tt ′ S′ S u r O′ O′ O S′ u r B 时钟 与时钟 相遇时 O′ O 0 = tt 11 ′ = 时钟 与时钟 相遇时 O′ B 时钟 O′ 2t′ 时钟 2 B t 12 Δ = − ttt t >Δ Δτ 运动时钟的变慢! S 系上的观察者认为运动时钟走得比静止时钟慢一些 物体 S ′系内的一个时钟 O′