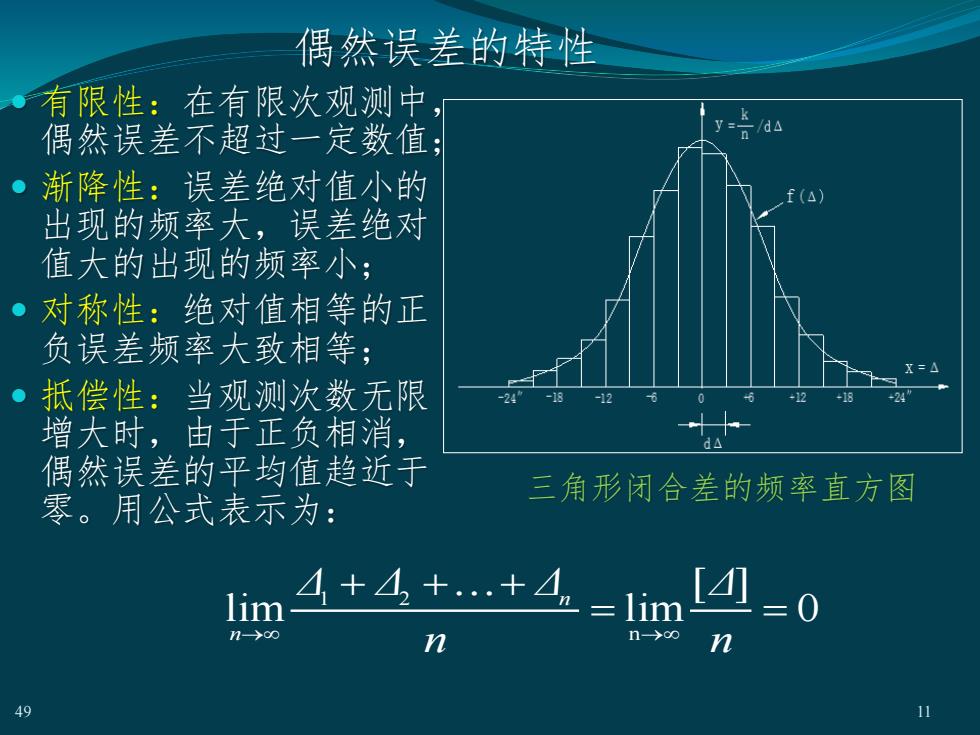
偶然误差的特性有限性:在有限次观测中-V=n偶然误差不超过一定数值渐降性:误差绝对值小的f(a)出现的频率大,误差绝对值大的出现的频率小:对称性:绝对值相等的正负误差频率大致相等;X=A抵偿性:当观测次数无限-2424-18-12+18增大时,由于正负相消,偶然误差的平均值趋近于三角形闭合差的频率直方图零。用公式表示为:4+4+..+4limlimn>0n->0nn4911
偶然误差的特性 有限性:在有限次观测中, 偶然误差不超过一定数值; 渐降性:误差绝对值小的 出现的频率大,误差绝对 值大的出现的频率小; 对称性:绝对值相等的正 负误差频率大致相等; 抵偿性:当观测次数无限 增大时,由于正负相消, 偶然误差的平均值趋近于 零。用公式表示为: 49 11 三角形闭合差的频率直方图 0 [ ] lim lim n 1 2 = = + ++ → → n Δ n Δ Δ Δ n n

正态分布曲线以及标准差和方差在统计理论上如果观测次数无限增多(n一→8),而误差区间又无限缩小,则频率直方图成为一条光滑的曲线,在统计学中称为偶然误差的“正态分布曲线”其数学方程式为:202f()V2元0式中参数称为“标准差”,其平方。2称为“方差”方差为偶然误差(真误差)平方的理论平均值:4+4+...+4[4lim"=limnn-0000[4]44]标准差的计算式:=limvlimnnn→00n>004912
正态分布曲线以及标准差和方差 49 12 2 2 2 2π 1 ( ) − f Δ = e σ n ΔΔ n Δ n n [ ] [ ] lim lim 2 → → = = n Δ n Δ Δ Δ n n n [ ] 2 2 2 2 2 2 1 lim → lim → = + + + = 在统计理论上如果观测次数无限增多(n→∞),而 误差区间dΔ又无限缩小,则频率直方图成为一条光滑的 曲线,在统计学中称为偶然误差的“正态分布曲线”, 其数学方程式为: 式中参数σ称为“标准差” ,其平方σ 2 称为“方差” , 方差为偶然误差(真误差)平方的理论平均值: 标准差的计算式:

85-2评定测量精度的标准一、中误差用标准差衡量测量观测成果的精度,在理论上是严格和合理的。但在实际测量工作中,不可能对某一量进行无穷多次观测。因此,定义:根据有限次观测的偶然误差用标准差计算式求得的称为“中误差”,其计算式为:4+4+...+44m=土nn选择两组三角形内角之和的观测值,求得三角形角度闭合差,分别按上式在表5-2中计算中误差,得到:第2组:mz= ±3.6第1组: m= ±2. 7″可见第1组的观测精度高于第2组。4913
§5-2 评定测量精度的标准 一、中误差 49 13 用标准差衡量测量观测成果的精度,在理论上是严格和 合理的。但在实际测量工作中,不可能对某一量进行无 穷多次观测。因此,定义:根据有限次观测的偶然误差, 用标准差计算式求得的称为“中误差”,其计算式为: n ΔΔ n Δ Δ Δ m [ ] 2 n 2 2 2 1 = + ++ = 选择两组三角形内角之和的观测值,求得三角形角度闭 合差,分别按上式在表5-2中计算中误差,得到: 第1组: m1= ±2.7″ 第2组: m2= ±3.6″ 可见第1组的观测精度高于第2组
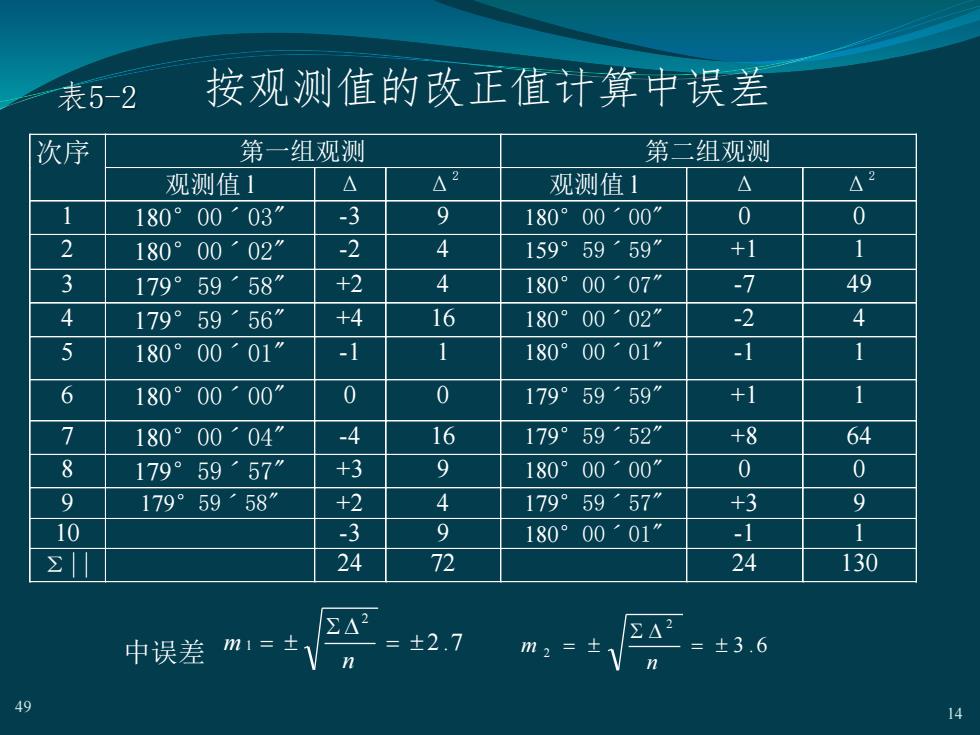
按观测值的改正值计算中误差表5-2次序第一组观测第二组观测4242△A观测值1观测值1-390010003180°0000180°2-24159″+102”159°59180°003449+2-75958″0007"180°179°4416-2+40002"5956"180°179°511-101"-1180°0001"001806001+100*005959180°179°7-41659+864179°52°0004"180°8900+30000”5957"180°179°949+257"+35958”179°59179°9110-1-301"00180°2472241302422A2=±2.7ml=±=±3.6土m2=中误差nn4914
按观测值的改正值计算中误差 次序 第一组观测 第二组观测 观测值 l Δ Δ2 观测值 l Δ Δ2 1 180°00ˊ03" -3 9 180°00ˊ00" 0 0 2 180°00ˊ02" -2 4 159°59ˊ59" +1 1 3 179°59ˊ58" +2 4 180°00ˊ07" -7 49 4 179°59ˊ56" +4 16 180°00ˊ02" -2 4 5 180°00ˊ01" -1 1 180°00ˊ01" -1 1 6 180°00ˊ00" 0 0 179°59ˊ59" +1 1 7 180°00ˊ04" -4 16 179°59ˊ52" +8 64 8 179°59ˊ57" +3 9 180°00ˊ00" 0 0 9 179°59ˊ58" +2 4 179°59ˊ57" +3 9 10180 °00ˊ03" -3 9 180°00ˊ01" -1 1 Σ|| 24 72 24 130 中误差 2 .7 2 1 = = n m 3 .6 2 2 = = n m 49 14 表5-2
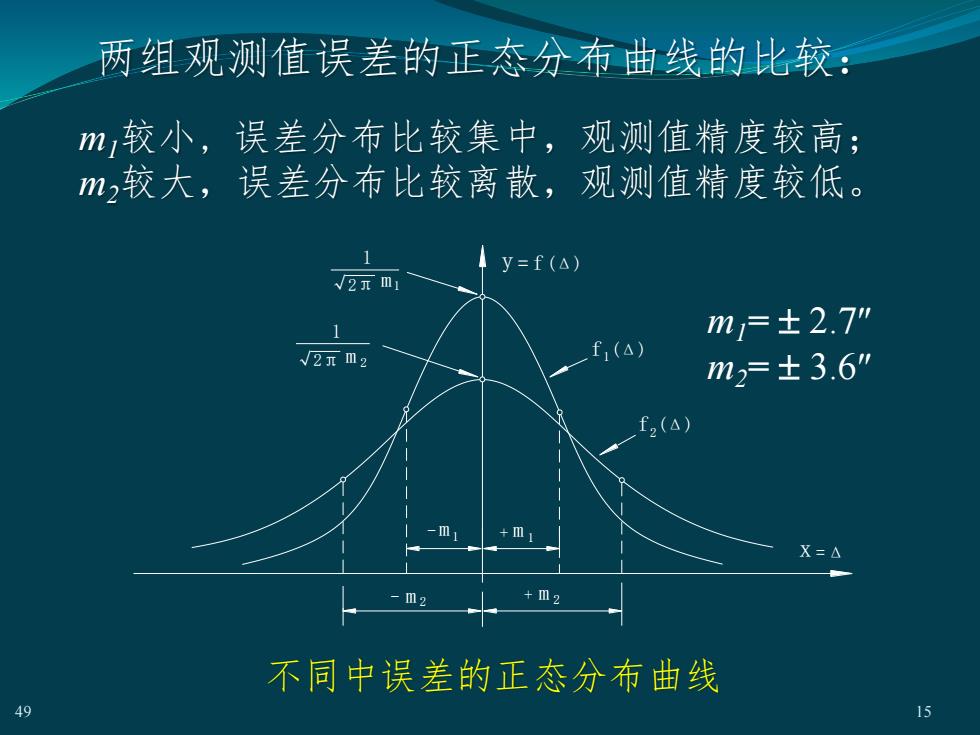
两组观测值误差的正态分布曲线的比较m较小,误差分布比较集中,观测值精度较高:m较大,误差分布比较离散,观测值精度较低。y=f(A)V2元m1mj=±2.7"f,(△)V2元m2m2=±3.6"f,(A)-m+mX=A+m2-m2不同中误差的正态分布曲线4915
m1较小, 误差分布比较集中,观测值精度较高; m2较大,误差分布比较离散,观测值精度较低。 两组观测值误差的正态分布曲线的比较: m1= 2.7 m2= 3.6 x =Δ = y f (Δ) f (Δ) f (Δ) m 1 m 1 m 2 m 2 1 2 m1 m 2 + + - - √2π √2π 1 1 49 15 不同中误差的正态分布曲线