
(二)偶然误差在相同的观测条件下,对某一量进行一系列观测,误差出现的符号和数值大小都不相同,从表面看没有任何规律性,这种误差称为“偶然误差”,是由许多无法精确估计的因素综合造成(人的分辨能力,仪器的极限精度,天气的无常变化,以及环境的干扰等)。偶然误差不可避免,但在一定条件下的大量的偶然误差,在实践中发现具有统计学规律。偶然误差举例:仪器对中误差,气泡居中判断、目标瞄准、度盘读数等误差,气象变化等外界环境等影响观测。(三)粗差由于观测者的粗心大意,或某种特别大的于扰而产生较大的误差称为“粗差”(俗称错误),应避免和舍弃粗差496
在相同的观测条件下,对某一量进行一系列观测,误 差出现的符号和数值大小都不相同,从表面看没有任何 规律性,这种误差称为“偶然误差” ,是由许多无法精 确估计的因素综合造成(人的分辨能力,仪器的极限精度, 天气的无常变化,以及环境的干扰等)。 偶然误差不可避免,但在一定条件下的大量的偶然误 差,在实践中发现具有统计学规律。 (三)粗差 由于观测者的粗心大意,或某种特别大的干扰而产生较 大的误差称为“粗差”(俗称错误),应避免和舍弃粗差。 偶然误差举例:仪器对中误差,气泡居中判断、目标瞄 准、度盘读数等误差,气象变化等外界环境等影响观测。 49 6 (二)偶然误差

(四)误差处理原则系统误差一找出发生规律,用观测方法和加改正值等方法抵消偶然误差一用多余观测减少其影响,利用几何条件检核,用“限差”来限制。粗差一细心观测,用多余观测和几何条来件来发现,将含有粗差的观测值剔除。49
(四)误差处理原则 49 7 粗 差 — 细心观测,用多余观测和几何条 来件来发现,将含有粗差的观测 值剔除。 系统误差 — 找出发生规律,用观测方法和 加改正值等方法抵消。 偶然误差 — 用多余观测减少其影响,利用 几何条件检核,用“限差”来 限制

三、偶然误差的特性偶然误差的定义设某一量的真值为X,对该量进行n次观测,得n个观测值lj,l2,…,ln,产生n个真误△1,2,…,△△, =X-l真值与观测值之差定义为“真误差”,真误差属于偶然误差,但真值必须已知才能求得真误差。测量的观测和计算中,在一般情况下真值是不知道的,只能根据几何条件等间接知道真值,例如三角形三个内角之和为180°(真值),而三个内角的观测值之和也可以作为一个独立的观测值,据此求得三内角之和的真误差(称为三角形角度闭合差)。49
三、偶然误差的特性 偶然误差的定义 设某一量的真值为X,对该量进行 n 次观测,得n 个观测值 ,产生n个真误 i i = X −l 49 8 l1 , l2 ,., ln Δ1,Δ2,.,Δ n 真值与观测值之差定义为“真误差”,真误差属于偶然 误差,但真值必须已知才能求得真误差。测量的观测和 计算中,在一般情况下真值是不知道的,只能根据几何 条件等间接知道真值,例如三角形三个内角之和为180° (真值),而三个内角的观测值之和也可以作为一个独立 的观测值,据此求得三内角之和的真误差(称为三角形 角度闭合差)

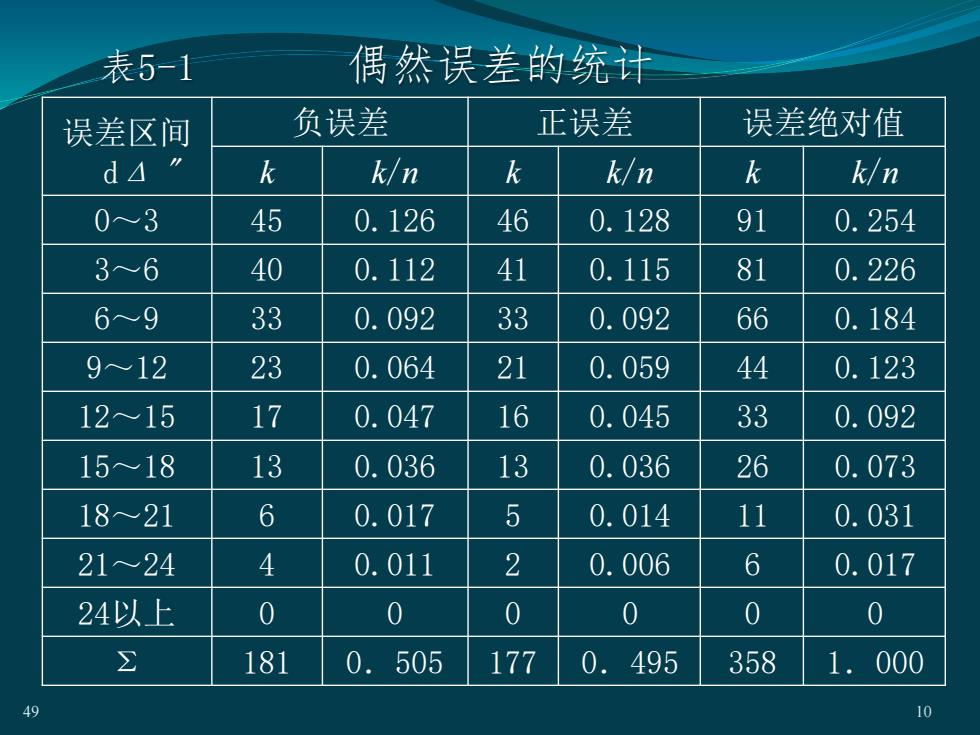
多次观测中寻找偶然误差的规律:对358个三角形在相同的观测条件下观测了全部内角,三角形内角之和的真值为180°,观测值为三个内角之和(α+β+),因此其真误差(三角形闭合差)为:△,=180° - (α;+ β,+ )观测数据统计结果列于V表5-1,据此分析三角形内角和的真误差,的分布规律。βα49
多次观测中寻找偶然误差的规律: 对358个三角形在相同的观测条件下观测了全部内角, 三角形内角之和的真值为180°,观测值为三个内角之和 (i +i+ i ),因此其真误差(三角形闭合差)为: i = 180°– ( i + i+ i ) 观测数据统计结果列于 表5-1,据此分析三角形 内角和的真误差 i 的 分布规律。 49 9
偶然误差的统计表5-1负误差正误差误差绝对值误差区间"kkkk/nk/nk/nd△4591460~30.1280.2540.1268140413~60.1120.1150.2263333666~90.0920.0920.1842321449~120.0640.0590.12317163312~150.0470.0450.09213132615~180.0360.0360.07365110.01418~210.0170.03142621~240. 0110.0060.01700000024以上Z1810.5051770.43584951.0001049
表5-1 偶然误差的统计 49 10 误差区间 dΔ " 负误差 正误差 误差绝对值 k k/n k k/n k k/n 0~3 45 0.126 46 0.128 91 0.254 3~6 40 0.112 41 0.115 81 0.226 6~9 33 0.092 33 0.092 66 0.184 9~12 23 0.064 21 0.059 44 0.123 12~15 17 0.047 16 0.045 33 0.092 15~18 13 0.036 13 0.036 26 0.073 18~21 6 0.017 5 0.014 11 0.031 21~24 4 0.011 2 0.006 6 0.017 24以上 0 0 0 0 0 0 Σ 181 0.505 177 0.495 358 1.000