
一、循环码的数学概念 (2)证g(x)x-1,则g(x)一定生成一个[n,k]循环码(课本证得不好) g(x)的倍式h(x)g(x)组成一个理想V,由定理1,V为循环码。 下证V的维数为k. 先证g(x),xg(x),x2g(x),,xk-1g(x)线性无关。 mog(x)+m:xg(x)+m2x2g(x)+...+mxxg(x)= )-m() 次数小于n,模xn1不为零,所以g(x),xg(x),x2g(x),.,xk1g(x)线性无关。 又g(x)|(xn-1),设xn-1=h(x)g(x),6h(x)=k=n-6°g(x) 任c(x)∈y有c(x)=q(x)g(x), q (x)=p (x)h(x)+r(x),gr(x)<k c(x)=[p(x)h(x)+r(x)]g(x)=p(x)(xh-1)+r(x)g(x) c(x)≡r(x)g(x) mod xn-1 k- =(2rxg() i=0 =是rg g(x),xg(x),x2g(x),,xk-1g(x)是V的一组基
一、循环码的数学概念 (2)证g(x)|xn-1,则g(x)一定生成一个[n,k]循环码(课本证得不好) g(x)的倍式h(x)g(x)组成一个理想V,由定理1,V为循环码。 下证V的维数为k. 先证g(x),xg(x),x2g(x),…,xk-1g(x)线性无关。 m g(x) m xg(x) m x g(x) m x g(x) ( ) ( ) ( ) 1 0 k-1 k-1 2 0 1 2 m x g x m x g x k i i i = + + ++ = − = 次数小于n,模x n -1不为零,所以g(x),xg(x),x2g(x),…,xk-1g(x)线性无关。 又g(x)|(x n-1),设x n-1 =h(x)g(x), h(x)=k= n- g(x) 任c(x)V,有c(x)=q(x)g(x), 设q(x)=p(x)h(x)+r(x), r(x)<k c(x)=[p(x)h(x)+r(x)]g(x)=p(x)(xn-1)+r(x)g(x) c(x)≡r(x)g(x) mod xn-1 ( ) − = − = 1 0 1 0 ( ) ( ) ( ) k i i i k i i i r x g x r x g x g(x),xg(x),x2g(x),…,xk-1g(x)是V的一组基

二、xn-1的因式分解 由上面的分析可知,要构造一个F,上[n,灯循环码,关键是要 找到生成多项式g(x),而g(X是x-1的mk次因式. 因此对xn 1的因式分解是构造循环码的关键问题, 1. 当n=g-1 根据第四章定理17,把(1)式共轭根的一次因式相乘,得最 小多项式(F,上,是素多项式),所以 x-1=I I-B:)=II(x-w,")=Im.(x) s=1B为GF(pm)中 s=1i=0 S= 第s个共扼根系的 第个共扼根 其中,r为w对模n的方次数,n为m,的级数,m(x)为第s个共扼根 系共扼根对应的最小多项式 特别地,当n=2m-1,n-k=m(g(x)的次数为m时,可查表求GF(2)上 的m次本原多项式p(x),由第四章定理20(课本定理4.6.7,p144)可知, p(x)|x-l,可以证明(参看华工出版社R.E.Blahut《差错控制码的理 论与实践》,p.85),由p(x)生成的循环码止3,因此是一个汉明码:
二、x n -1的因式分解 由上面的分析可知, 要构造一个Fq上[n, k]循环码, 关键是要 找到生成多项式g(x), 而g(x)是x n -1的n-k次因式. 因此对x n - 1的因式分解是构造循环码的关键问题. 1. 当n = q m-1 根据第四章定理17,把(1)式共轭根的一次因式相乘,得最 小多项式(Fp上,是素多项式),所以 = = = = − − = − = − = v s s v s r i p s v s i s GF p s i p x x x w m x i s m i m 1 ( ) 1 0 1 1 1 ( ) ( ) ( ) 第 个共扼根 第 个共扼根系的 为 中 其中,r为ws对模n的方次数,n为ws的级数,ms(x)为第s个共扼根 系共扼根对应的最小多项式 特别地, 当n = 2 m -1, n -k =m (g(x)的次数为m)时, 可查表求GF(2)上 的m次本原多项式p(x), 由第四章定理20(课本定理4.6.7, p144)可知, p(x)|x n -1, 可以证明(参看华工出版社R.E. Blahut 《差错控制码的理 论与实践》,p.85), 由p(x)生成的循环码d=3, 因此是一个汉明码
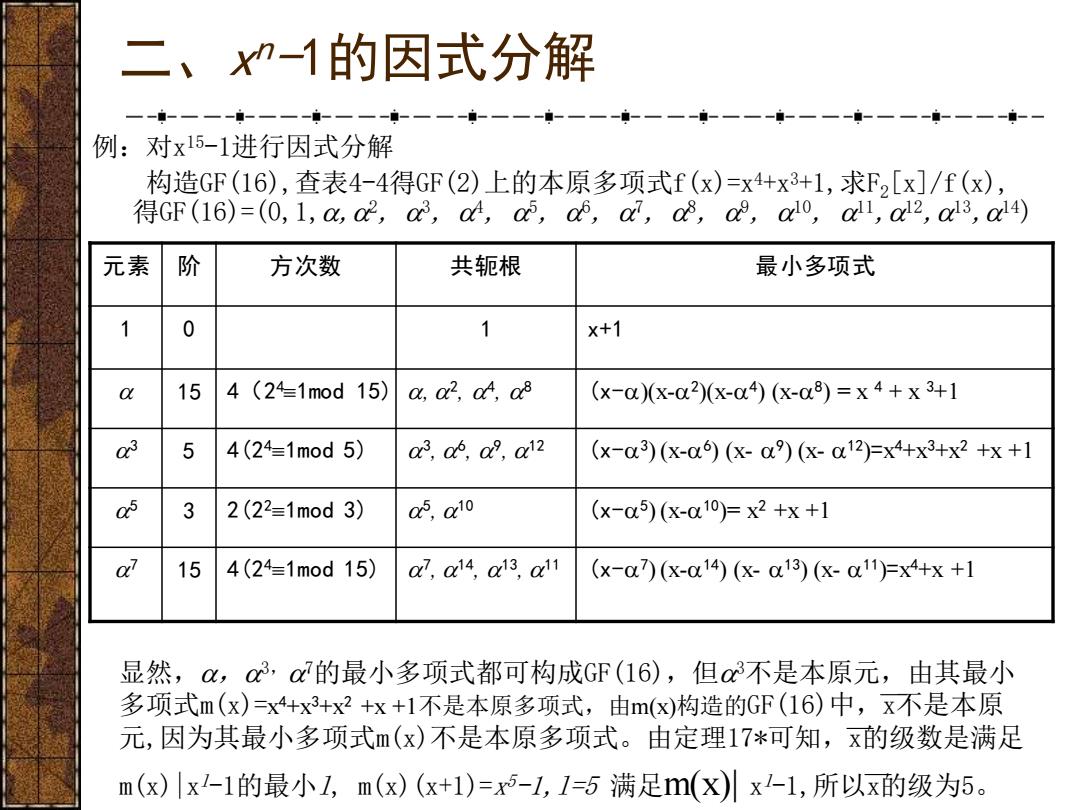
二、xn-1的因式分解 例:对x15-1进行因式分解 构造GF(16),查表4-4得GF(2)上的本原多项式f(x)=x4+x3+1,求F2[x]/f(x), 得GF(16)=(0,1,0,a2,a心,a,a,a,a,a,a,a0,a1,a2,a3,al4) 元素 阶 方次数 共轭根 最小多项式 1 0 1 x+1 a 15 4(24=1mod15) a,a2,a,as (x-)(x-02)(x-04)(X-08)=X4+x3+1 a3 5 4(24=1mod5) as,as,a,aiz (x-a3)(x-0)(x-)(x-a12)=x+x3+x2+x+1 as 3 2(22=1mod3) a,a10 (x-05)(X-010))=x2+x+1 a 15 4(24=1mod15) a7,a14,a13,a11 (x-0)(X-014)(X-13)(X-011)=x4+x+1 显然,,a心,a的最小多项式都可构成GF(16),但a心不是本原元,由其最小 多项式m(x)=x4+x3+x2+x+1不是本原多项式,由m(x)构造的GF(16)中,x不是本原 元,因为其最小多项式m(x)不是本原多项式。由定理17*可知,x的级数是满足 m(x)x-1的最小1,m(x)(x+1)=x-1,1=5满足m(X)x-1,所以x的级为5
二、x n -1的因式分解 例:对x 15-1进行因式分解 构造GF(16),查表4-4得GF(2)上的本原多项式f(x)=x4+x3+1,求F2[x]/f(x), 得GF(16)=(0,1,,2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12,13,14) 元素 阶 方次数 共轭根 最小多项式 1 0 1 x+1 15 4(2 41mod 15) , 2 , 4 , 8 (x-)(x-2 )(x-4 ) (x-8 ) = x 4 + x 3+1 3 5 4(241mod 5) 3 , 6 , 9 , 12 (x-3 ) (x-6 ) (x- 9 ) (x- 12)=x 4+x3+x2 +x +1 5 3 2(221mod 3) 5 , 10 (x-5 ) (x-10)= x 2 +x +1 7 15 4(241mod 15) 7 , 14 , 13 , 11 (x-7 ) (x-14) (x- 13) (x- 11)=x 4+x +1 显然,,3,7的最小多项式都可构成GF(16),但3不是本原元,由其最小 多项式m(x)=x 4+x3+x2 +x +1不是本原多项式,由m(x)构造的GF(16)中,x不是本原 元,因为其最小多项式m(x)不是本原多项式。由定理17*可知,x的级数是满足 m(x)|xl -1的最小l, m(x)(x+1)=x 5 -1,l=5 满足m(x)| x l -1,所以x的级为5

二、x-1的因式分解 X15-1=(x+1)(x4+x3+1)(x4+x3+x2+x+1)(x2+x+1)(x4+x+1) 可以任意组合,共有 C+C?+C+C+C+1(g(x)=1的情况)=5+10+10+5+1+1=32 种组合,即共有32个循环码 例如,g(x)F(x4+x3+x2+x+1)(x4+x+1)=x8+x+x+x4+1 构成[15,7]循环码,而g(x)的重量为5,所以d<=5(实际上等于5) 2. 当n≠qm-1,但nlqm-1 可在中找阶为n的元素B,则B生成的n阶循环群含有x"-l=O的全部根 3. 问题:1肯定为xm-1的根,所以(x+1)川xm-1 x-1=(x+1)(x-1+xm-2+..+x+1) 所以g1()=(x+1),g2(X=(x-1+xm-2+.+x+1) g()生成[n,n-1]码,2(x)生成[n,1]码 问g1(X)和g2(x)各生成什么码?
二、x n -1的因式分解 X 15-1=(x+1)(x 4 + x 3+1)(x 4+x3+x2 +x +1)(x 2 +x +1)(x 4+x +1) 可以任意组合,共有 1( ( ) 1 5 10 10 5 1 1 32 5 5 4 5 3 5 2 5 1 C5 +C +C +C +C + g x = 的情况)= + + + + + = 种组合,即共有32个循环码 例如,g(x)= (x 4+x3+x2 +x +1)(x 4+x +1)= x 8+x7+x6 +x4 +1 构成[15,7]循环码,而g(x)的重量为5,所以d<=5(实际上等于5) 2. 当n q m-1, 但n |q m-1 可在中找阶为n的元素, 则生成的n阶循环群含有x n -1=0的全部根. 3. 问题:1肯定为x n -1的根,所以(x+1)| xn -1 x n -1=(x+1)(xn-1+xn-2+…+x+1) 所以g1 (x)=(x+1), g2 (x)= (xn-1+xn-2+…+x+1) g1 (x)生成[n,n-1]码,g2 (x)生成[n,1]码 问g1 (x)和g2 (x)各生成什么码?

三、循环码的校验矩阵H和生成矩阵G 由于g(x,Xg(x),,“1g(?是k个线性无关的码字,所以生 成矩阵G为 x-g(x) ·. G= (1) xg(x) g(x) *x训n1,设x-1=g()h(为,h(x)=∑hx 称为码校验多项式, i=0 其反多项式片(x=之hx,取 x"-k-h(x) H= xh(x) (2) h(x) 可证HG=O,所以(2)确定的H是校验矩阵
三、循环码的校验矩阵H 和生成矩阵G 由于g(x), x g(x), ..., x k-1 g(x)是k个线性无关的码字, 所以生 成矩阵G为 = − ( ) ( ) ( ) 1 g x xg x x g x G k (1) g(x)| x n -1,设x n -1=g(x)h(x), h(x) = 称为码校验多项式, 其反多项式h *(x) = ,取 = k i i i h x 0 = − k i k i i h x 0 = − − ( ) ( ) ( ) * * 1 * h x xh x x h x H n k (2) 可证HG T=0, 所以(2)确定的H是校验矩阵