
一、循环码的数学概念 1. 定义1(循环码):若线性码C=[n,]满足 廿(Cn-1 Cn2,cc)∈C:(cn2,c,ccn-)∈C,则称为循环码。 若用线性空间描述,则n重子空间Vn,k∈Vm,若 Vv=(cn-n cn-2...,cn co)EVn,k:Vv=(cn-2...,cn co cn-)EVn,k 则称Vn,k为循环子空间,也称[n,k]循环码。 g(x) (0001101) 例[7,4]汉明码,p62,例3.3 xg(x) (0011010) x2g(x) (0110100) 0001111 xg(x) (1101000) H=0110011 x'g(x) (1010001) x5g(x) (0100011) 1010101 xg(x) (1000110) (x+1)g(x) (0010111) x(x+1)g(x) (0101110) x2(x+1)g(x) (1011100) x3(x+1)g(x) (0111001) x4(x+1)g(x) (1110010) x5(x+1)g(x) (1100101) x6(x+1)g(x) (1001011) (x3+x+1)g(x) (1111111 0*g(x) (0000000)
一、循环码的数学概念 1. 定义1 (循环码) :若线性码C = [n,k]满足 (cn-1,cn-2,...,c1,c0)C:(cn-2,...,c1,c0,cn-1)C, 则称为循环码。 若用线性空间描述,则n重子空间Vn,k Vn,若 v=(cn-1,cn-2,...,c1,c0)Vn,k:v=(cn-2,...,c1,c0,cn-1)Vn,k 则称Vn,k为循环子空间,也称[n,k]循环码。 g(x) (0 0 0 1 1 0 1) xg(x) (0 0 1 1 0 1 0) x 2g(x) (0 1 1 0 1 0 0) x 3g(x) (1 1 0 1 0 0 0) x 4g(x) (1 0 1 0 0 0 1) x 5g(x) (0 1 0 0 0 1 1) x 6g(x) (1 0 0 0 1 1 0) (x+1)g(x) (0 0 1 0 1 1 1) x(x+1)g(x) (0 1 0 1 1 1 0) x 2(x+1)g(x) (1 0 1 1 1 0 0) x 3(x+1)g(x) (0 1 1 1 0 0 1) x 4(x+1)g(x) (1 1 1 0 0 1 0) x 5(x+1)g(x) (1 1 0 0 1 0 1) x 6(x+1)g(x) (1 0 0 1 0 1 1) (x3+x+1)g(x) (1 1 1 1 1 1 1) 0*g(x) (0 0 0 0 0 0 0) 例[7,4]汉明码,p62,例3.3 = 1 0 1 0 1 0 1 0 1 1 0 0 1 1 0 0 0 1 1 1 1 H
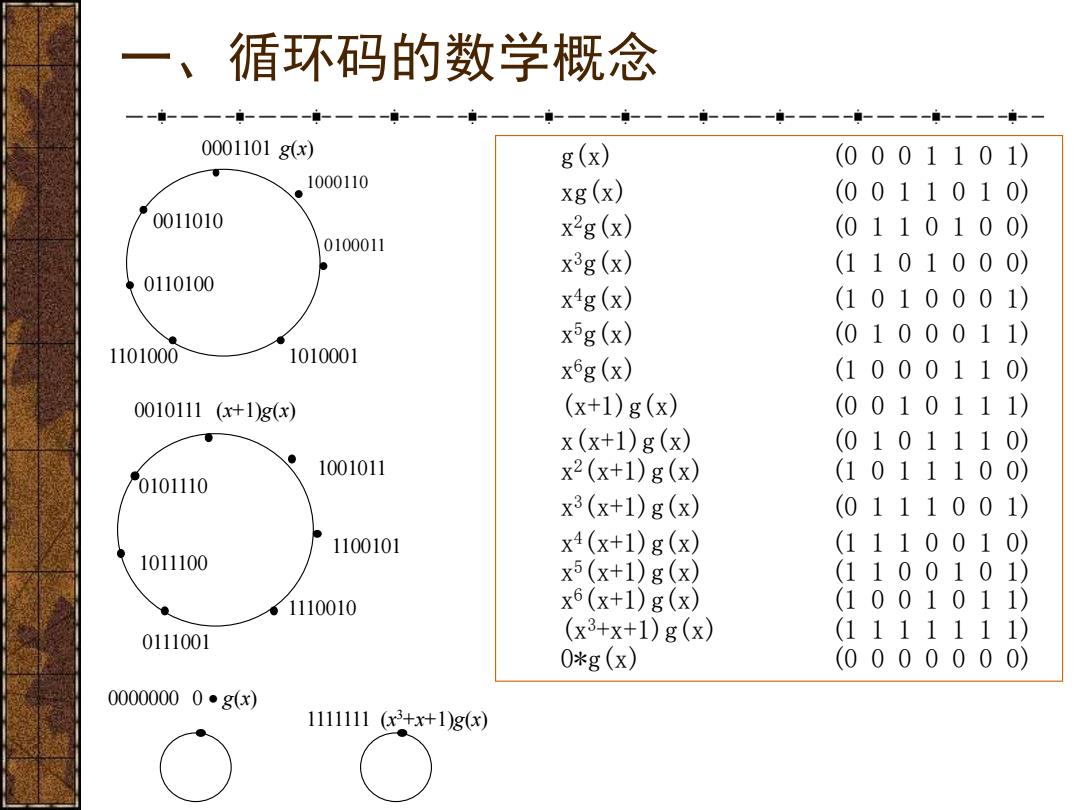
一、循环码的数学概念 --一一--一一--一一- 0001101gx) g(x) (0001101) ◆ 1000110 xg(x) (0011010) 0011010 x2g(x) (0110100) 0100011 xig(x) (1101000) 0110100 x4g(x) (1010001) x5g(x) (0100011) 1101000 1010001 x6g(x) (1000110) 0010111(x+1)g(x) (x+1)g(x) (0010111) x(x+1)g(x) (0101110) 1001011 (1011100) 0101110 x2(x+1)g(x) x3(x+1)g(x) (0111001) 1100101 x4(x+1)g(x) (1110010) 1011100 x5(x+1)g(x) (1100101) 1110010 x6(x+1)g(x) (1001011) 0111001 (x3+x+1)g(x) (1111111) 0*g(x) (0000000) 00000000●g(x) 1111111(x3+x+1)g(x)
一、循环码的数学概念 0100011 1000110 0001101 g(x) 1101000 0011010 0110100 1010001 0010111 (x+1)g(x) 0111001 0101110 1011100 1110010 1100101 1001011 0000000 0 • g(x) 1111111 (x 3+x+1)g(x) g(x) (0 0 0 1 1 0 1) xg(x) (0 0 1 1 0 1 0) x 2g(x) (0 1 1 0 1 0 0) x 3g(x) (1 1 0 1 0 0 0) x 4g(x) (1 0 1 0 0 0 1) x 5g(x) (0 1 0 0 0 1 1) x 6g(x) (1 0 0 0 1 1 0) (x+1)g(x) (0 0 1 0 1 1 1) x(x+1)g(x) (0 1 0 1 1 1 0) x 2(x+1)g(x) (1 0 1 1 1 0 0) x 3(x+1)g(x) (0 1 1 1 0 0 1) x 4(x+1)g(x) (1 1 1 0 0 1 0) x 5(x+1)g(x) (1 1 0 0 1 0 1) x 6(x+1)g(x) (1 0 0 1 0 1 1) (x3+x+1)g(x) (1 1 1 1 1 1 1) 0*g(x) (0 0 0 0 0 0 0)

一、循环码的数学概念 数学上,码字循环是码多项式乘x(左循环)或x1(右循环)取模x-的余式 类 定理1:设V,是模x-剩余类构成的线性空间,Vnkc'n,'n是一个循环 码的充要条件是:V是x-1剩余类中的理想 分析:理想的定义:交换环中的非空子集/称为中的理想,若: 1)Ha,b∈1:a-b∈I; 2)Ha∈,r∈R:ar=ra∈I 证明:()证'是一个循环码,则'是x-1剩余类中的理想 n网ea,7=2ey,证7网网ey f网田=2r i=0 v(x)=(an an2a,ao)EVnk xv(x)=(an2,..an,do,an)EVnk +“+4 x'v(x)=(aiadoaan)EV.k ∴.fx)v(x)=v(x)•f(x)eVn
一、循环码的数学概念 数学上,码字循环是码多项式乘x(左循环)或x -1 (右循环)取模x n -1的余式. 定理1:设Vn是模x n -1剩余类构成的线性空间,Vn,k Vn, Vn,k是一个循环 码的充要条件是: Vn,k是x n -1剩余类中的理想 。 分析:理想的定义: 交换环R中的非空子集I称为R中的理想,若: 1) a, b I: a-b I; 2) a I, r R: ar =ra I 证明:(1)证Vn,k是一个循环码,则Vn,k是x n -1剩余类中的理想 n k n i n n i n k i n n n k n n n k n i i i n n k n i i n k i f x v x v x f x V x v x a a a a a V x v x a a a a V v x a a a a V f x v x f x v x v x V f x f x V f x v x V , 1 1 0 1 , 2 1 0 1 , 1 2 1 0 , 1 0 , 1 0 , ( ) ( ) ( ) ( ) ...... ( ) ( ,..., , , ,..., ) ...... ( ) ( ,..., , , ) ( ) ( , ,..., , ) ( ) ( ) ( ) ( ) , ( ) , ( ) ( ) • = • = = = • = = • − − − − − − − − − = − = 证

一、循环码的数学概念 (2)证'n是x-1剩余类中的理想,则V,是一个循环码 v(x)∈'nk:xv(x)=x(x)∈'nk 理想,某些元素的倍式组成,可以证明,V仅由一个元素生成, 是个主理想 定理2:GF(q)上的循环码'nk中,存在唯一的n-k次首一多项式 86)=xn-k+gn-kx-1++gx+g0,使: 1)vc(x):g(x)Ic(x); 2) cy∈Fg[x:oc(x)sn-1且gxlc(x)->c(x)∈Vnki 1)说明每一个码矢都是g(x)的倍式,即由g(x)循环移位的线 性组合 2)说明g(x)小于n-1次的倍式(即由g(x)循环移位的线性组合) 定是个码多项式。 gx)叫循环码的生成元(生成多项式),所以V是个主理想
一、循环码的数学概念 (2)证Vn,k是x n -1剩余类中的理想,则Vn,k是一个循环码 n k Vn k v x V xv x x v x , , ( ) : ( ) = ( ) ❖ 理想,某些元素的倍式组成,可以证明,Vn,k仅由一个元素生成, 是个主理想 ❖ 定理2:GF(q)上的循环码Vn,k中,存在唯一的n-k次首一多项式 g(x)=xn-k+gn-k-1x n-k-1+…+g1x+g0,使: 1) c(x) Vn,k: g(x)|c(x); 2) c(x) Fq [x]: c (x) n-1且g(x)|c(x) --> c(x) Vn,k; 1)说明每一个码矢都是g(x)的倍式, 即由g(x)循环移位的线 性组合 2)说明g(x)小于n-1次的倍式(即由g(x)循环移位的线性组合) 一定是个码多项式。 ❖ g(x)叫循环码的生成元(生成多项式),所以Vn,k是个主理想

一、循环码的数学概念 定理3:GF(q)上的[n,k]循环码的生成多项式g(x)|xn-1;反之,若g(x)|xn-1, 则g(x)一定生成一个[n,k]循环码,其中k=n-g(x) 证明:(1)证g(x)|xn-1 g(x)∈'nk 设xn-1=g(x)h(x)+r(x),°r(x)<°g(x)(欧几里德算法) 则 x”-1=g(x).h(x)+r(x)=0∈'nk r(x)=x”-1-g(x).h(x) 又g(x)h(x)∈Vnk ..r(x)EVnk 又a°r(x)<a°g(x) 而g(x)是生成元,次数最小,所以(x)=0
一、循环码的数学概念 定理3:GF(q)上的[n,k]循环码的生成多项式g(x)|xn-1;反之,若g(x)|xn-1, 则g(x)一定生成一个[n,k]循环码,其中k=n-g(x) 证明:(1)证g(x)|xn-1 g(x) Vn,k, 设x n-1=g(x)h(x)+r(x), r(x)< g(x) (欧几里德算法) 则 ( ) ( ) 0 ( ) ( ) ( ) ( ). ( ) ( ) 1 ( ). ( ) 1 ( ). ( ) ( ) 0 , , , = = − − − = + = g x r x r x g x r x V g x h x V r x x g x h x x g x h x r x V n k n k n n k n 而 是生成元,次数最小,所以 又 又