
Y.S.Han Introduction to Binary Linear Block Codes 15 Hamming Weight and Hamming Distance(1) 1.The Hamming weight (or simply called weight)of a codeword c,WH(c),is the number of 1's the nonzero components)of the codeword. 2.The Hamming distance between two codewords c and c'is defined as d(c,c')=the number of components in which c and c'differ. 3.dH(c,0)=WH(c). 4.Let HW be the set of all distinct Hamming weights that codewords of C may have.Furthermore,let HD(c)be the set of all distinct Hamming distances between c and any codeword. Then,HW HD(c)for any cC. 5.dH(c,c)=dH(c⊕c,O)=WH(c⊕c) 6.If C and C are equivalent to each other,then the HW for C School of Electrical Engineering Intelligentization,Dongguan University of Technology
Y. S. Han Introduction to Binary Linear Block Codes 15 Hamming Weight and Hamming Distance (1) 1. The Hamming weight (or simply called weight) of a codeword c, WH(c), is the number of 1’s ( the nonzero components) of the codeword. 2. The Hamming distance between two codewords c and c ′ is defined as dH(c, c′ ) = the number of components in which c and c ′ differ. 3. dH(c,0) = WH(c). 4. Let HW be the set of all distinct Hamming weights that codewords of C may have. Furthermore, let HD(c) be the set of all distinct Hamming distances between c and any codeword. Then, HW = HD(c) for any c ∈ C. 5. dH(c, c ′ ) = dH(c ⊕ c ′ , 0) = WH(c ⊕ c ′ ) 6. If C and C′ are equivalent to each other, then the HW for C School of Electrical Engineering & Intelligentization, Dongguan University of Technology

Y.S.Han Introduction to Binary Linear Block Codes 16 is the same as that for C.. 7.The smallest nonzero element in HW is referred to as dmin. 8.Let the column vectors of H be ho,h1,...,n-1). CHT (co:cI:...,cn-1)[ho hi...hn-1]T coho+cihi+..+cn-1hn-1 9.If c is of weight w,then cHT is a linear combination of w columns of I. 10.dmin is the minimum nonzero number of columns in H where a nontrivial linear combination results in zero. School of Electrical Engineering Intelligentization,Dongguan University of Technology
Y. S. Han Introduction to Binary Linear Block Codes 16 is the same as that for C′ . 7. The smallest nonzero element in HW is referred to as dmin. 8. Let the column vectors of H be {h0, h1, . . . , hn−1 }. cHT = (c0, c1, . . . , cn−1) [h0 h1 · · · hn−1] T = c0h0 + c1h1 + · · · + cn−1hn−1 9. If c is of weight w, then cHT is a linear combination of w columns of H. 10. dmin is the minimum nonzero number of columns in H where a nontrivial linear combination results in zero. School of Electrical Engineering & Intelligentization, Dongguan University of Technology

Y.S.Han Introduction to Binary Linear Block Codes 17 Hamming Weight and Hamming Distance (2) C={000000,100110,010101,001011, 110011,101101,011110,111000} HW =HD(c)={0,3,4}for all cC dH(001011,110011)=dH(111000,000000)=WH(111000)=3 School of Electrical Engineering Intelligentization,Dongguan University of Technology
Y. S. Han Introduction to Binary Linear Block Codes 17 Hamming Weight and Hamming Distance (2) C = {000000, 100110, 010101, 001011, 110011, 101101, 011110, 111000} HW = HD(c) = {0, 3, 4} for all c ∈ C dH(001011, 110011) = dH(111000, 000000) = WH(111000) = 3 School of Electrical Engineering & Intelligentization, Dongguan University of Technology
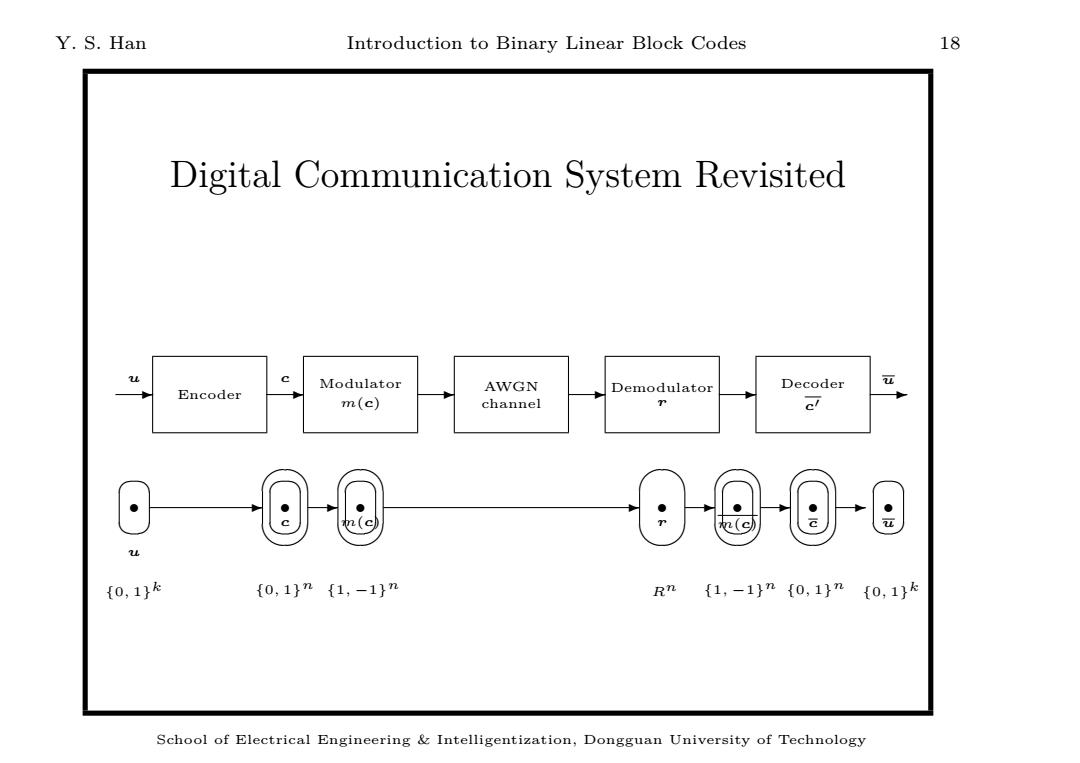
Y.S.Han Introduction to Binary Linear Block Codes 18 Digital Communication System Revisited u c Modulator Decoder Encoder AWGN Demodulator m(c) channel 2(c {0,1}k {0,1n{1,-1}n Rn {1,-1}n{0,1}n {0,1}k School of Electrical Engineering Intelligentization,Dongguan University of Technology
Y. S. Han Introduction to Binary Linear Block Codes 18 Digital Communication System Revisited Encoder Modulator m(c) AWGN channel Demodulator r Decoder ✲ u ✲ c ✲ ✲ ✲ c′ ✲ u ✞ ✝ ☎ ✆ r u {0, 1} k ✞ ✝ ☎ ✆ r ✎ ✍ ☞ c ✌ {0, 1} n ✞ ✝ ☎ ✆ r ✎ ✍ ☞ m(c) ✌ {1, −1} n ✲ ✲ ✎ ✍ ☞ ✌ ✎ ✍ ☞ ✌ ✎ ✍ ☞ ✌ ✞ ✝ ☎ ✆ ✞ ✝ ☎ ✆ ✞ ✝ ☎ ✆ r r r r r Rn m(c) {1, −1} n c {0, 1} n u {0, 1} k ✲ ✲ ✲ ✲ School of Electrical Engineering & Intelligentization, Dongguan University of Technology

Y.S.Han Introduction to Binary Linear Block Codes 19 Maximum-Likelihood Decoding Rule (MLD Rule)for Word-by-Word Decoding (1) 1.The goal of decoding: setc=ce where ces∈Cand Pr(celr)≥Pr(clr)for all c∈C. 2.If all codewords of C have equal probability of being transmitted,then to maximize Pr(cr)is equivalent to maximizing Pr(rc),where Pr(rc)is the probability that r is received when c is transmitted,since Pr(clr)=Pr(rle)Pr(c) Pr(r) 3.A maximum-likelihood decoding rule (MLD rule),which minimizes error probability when each codeword is transmitted equiprobably,decodes a received vector r to a codeword ce C School of Electrical Engineering Intelligentization,Dongguan University of Technology
Y. S. Han Introduction to Binary Linear Block Codes 19 Maximum-Likelihood Decoding Rule (MLD Rule) for Word-by-Word Decoding (1) 1. The goal of decoding: set cb = cℓ where cℓ∈ C and P r(cℓ|r) ≥ P r(c|r) for all c ∈ C. 2. If all codewords of C have equal probability of being transmitted, then to maximize P r(c|r) is equivalent to maximizing P r(r|c), where P r(r|c) is the probability that r is received when c is transmitted, since P r(c|r) = P r(r|c)P r(c) P r(r) . 3. A maximum-likelihood decoding rule (MLD rule), which minimizes error probability when each codeword is transmitted equiprobably, decodes a received vector r to a codeword cℓ∈ C School of Electrical Engineering & Intelligentization, Dongguan University of Technology