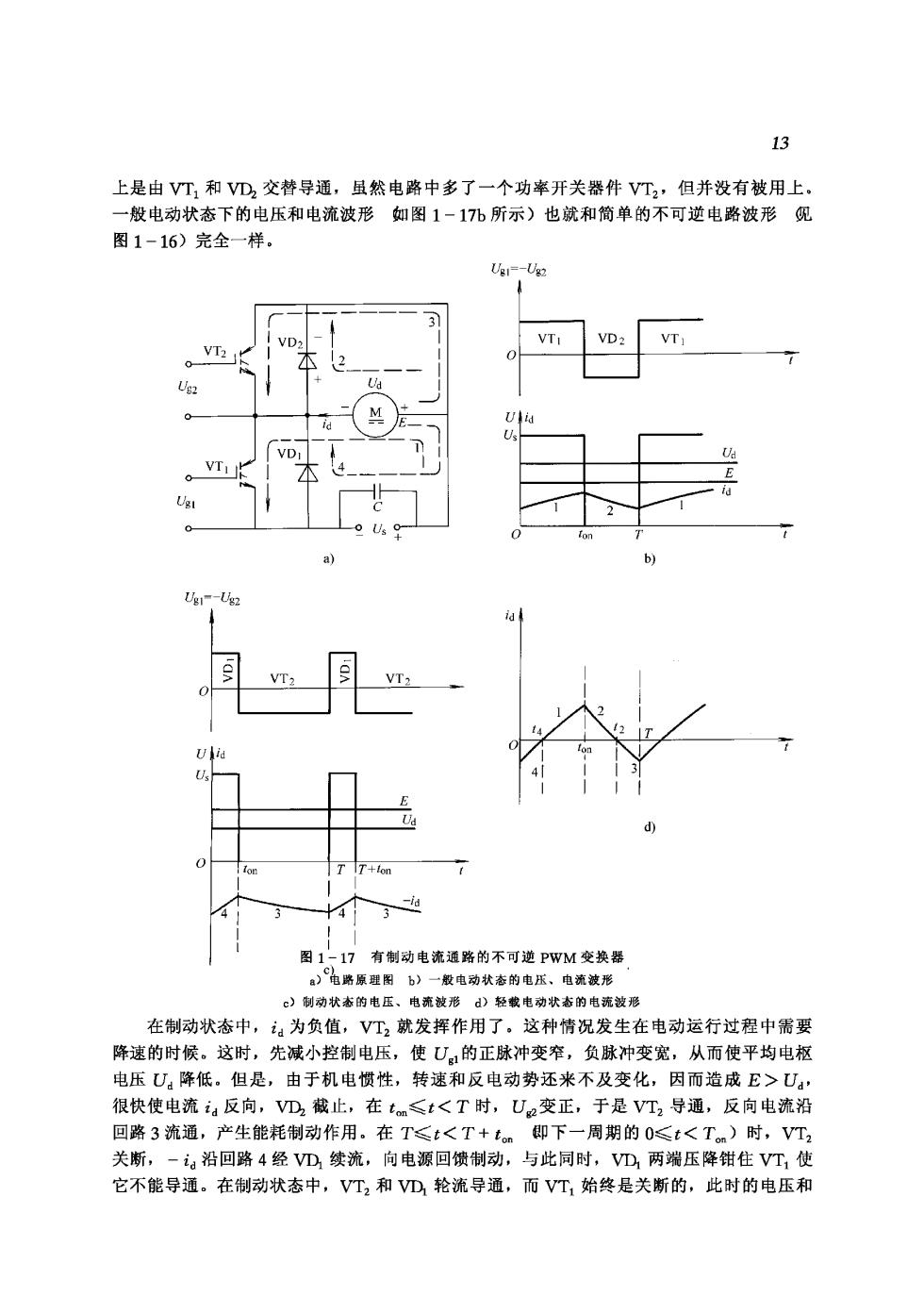
上是由VT,和VD2,交林导通,虽然电路中多了一个功率开关器件VT2,但并没有被用上 一般电动状态下的电压和电流波形如图1-17儿所示)也就和简单的不可逆电路波形见 图1-16)完全一样 1-U VTI VD2 VT 图1-17有制动电流通路的不可逆PwM变换器 )电路原理图b)一酸电动状态的电压、电流被形 ©》制动状态的电压、电流被形)轻载电动状态的电流被形 在制动状态中,为负值,V工2就发挥作用了,这种情况发生在电动运行过程中需要 降速的时候。这时,先减小控制电压,使U,的正脉冲变窄,负脉冲变宽,从而使平均电松 电压U降低。但是,由于机电惯性,转速和反电动势还米不及变化,因而造成E>U: 很快使电流a反向,VD2截止,在t≤t<T时,Ue变正,于是VT2导通,反向电流沿 回路3流通,产生能耗制动作用。在T≤t<T+t即下一周期的0≤t<T)时,VT 关断,-i妇沿回路4经VD续流,向电源回馈制动,与此同时,D,两端压降钳住VT,使 它不能导通。在制动状态中,VT2和VD,轮流导通,而VT始终是关断的,此时的电压和
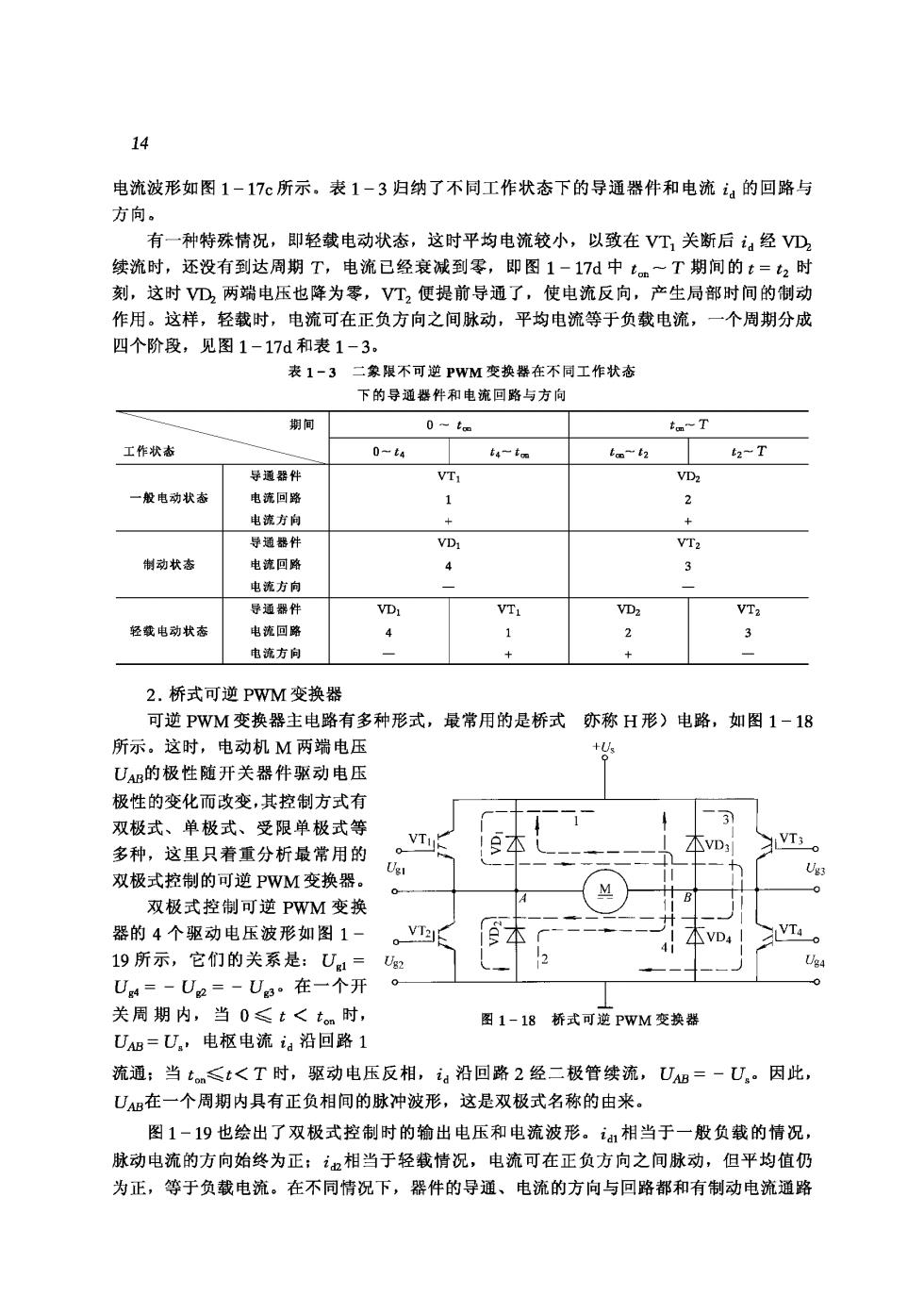
14 电流波形如图1-17c所示,表1-3归纳了不同工作状态下的导通器件和电流i妇的回路与 方向。 有一种特殊情况,即轻载电动状态,这时平均电流较小,以致在V工,关断后经VD 续流时,还没有到达周期T,电流已经衰减到零,即图1-17中t一T期间的t=2时 刻,这时D,两端电压也降为零,VT,便提前导通了,使电流反向,产生局部时间的制动 作用。这样, 轻载时,电流可在正负方向之间脉动, 平均电流等于负载电流, 个周期分成 四个阶段,见图1-17d和表1-3. 表1-3二象限不可逆PWM变换器在不同工作状态 下的导通器件和电流回路与方向 期间 0-t t。-T 工作状态 0-4 2~T VD 般电动状态 喇动状志 电流方 道都 3 3 轻电动状态 2.桥式可逆pWnM查换器 可逆PWM变换器主电路有多种形式, 最常用的是桥式亦称H形)电路,如图1-18 所示。这时,电动机M两端电压 UAg的极性随开关器件驱动电压 极性的变化而改变,其控制方式有 双极式、单极式、受限单极式笔 VT: 多种,这里只着重分析最常用的 T 双极式控制的可逆PWM变换器。 , 0 双极式控制可逆PWM变换 器的4个驱动电压波形如图1 19所示,它们的关系是:U= U=-Ua=-Ua·在-个开 关周期内,当0≤t<tm时, 图1-18桥式可逆PWM变换器 U=U,电枢电流a沿回路1 流通:当tn≤t<T时,驱动电压反相,a沿回路2经二极管续流,U加=一U。因此, UB在一个周期内具有正负相间的脉冲波形,这是双极式名称的由来。 图1-19也绘出了双极式控制时的输出电压和电流波形。相当于一般负载的情况, 脉动电流的方向始终为正:相当于轻载情况,电流可在正负方向之间脉动,但平均值仍 为正,等于负载电流。在不同情况下,器件的导通、电流的方向与回路都和有制动电流通路

15 的不可逆PWM变换器见图1-17)相似。电动机的正反转则体现在驱动电压正、负脉冲 的宽窄上。当正脉冲较宽时,>,则UAs的平均值为正,电动机正转,反之则反转 如果正、负脉冲相等,t=子,平均输出电压为 零,则电动机停止。图1-19所示的波形是电动机 正转时的情况。 双极式控制可逆PWM变换器的输出平均电压 为 -Tu=学- 4-18) 若占空比ρ和电压系数y的定义与不可逆变换器中 相同,则在双极式控制的可逆变换器中 Y=2p-1 1-19) 就和不可逆变换器中的关系不一样了, 谓速时,p的可调范围为0~1,相应地,Y -1一+1。当p>2时,y为正,电动机正转:当 p<}时,Y为负,电动机反转:当p=}时,7= 0,电动机停止。但电动机停止时电枢电压并不等 于零,而是正负脉宽相等的交变脉冲电压,因而电 流也是交变的。这个交变电流的平均值为零,不产 生平均转矩,徒然增大电动机的损耗,这是双极式 12 控制的缺点。但它也有好处,在电动机停止时仍有 高频微振电流,从而消除了正、反向时的静摩擦死 图1-19双极式控制可逆PWM变换器 的驱动电压、输出电压和电流波形 区,起着所谓动力润滑”的作用. 双极式控制的桥式可逆PWM变换器有下列优点: 1)电流一定连续。 2)可使电动机在四象限运行 3)电动机停止时有微振电流,能消除静摩擦死区。 4)低速平稳性好,系统的调速范固可达1:20000左右。 5)低速时,每个开关器件的驱动脉冲仍较宽,有利于保证器件的可靠导通 双极式控制方式的不足之处是:在工作过程中,4个开关器件可能都处于开关状态,开 关损耗大,而且在切换时可能发生上、下桥臂直通的事故,为了防止直通,在上、下桥臂的 驱动脉冲之间,应设置逻辑延时。为了克服上还缺点,可采用单极式控制,使部分器件处于 常通或常断状态,以减少开关次数和开关损耗,提高可靠性,但系统的静、动态性能会略有 降低。关于单极式控制,可参见参考文献巨,T]

16 1.3.2直流脉宽谓速系统的机械特性 由于采用了脉宽调制,严格地说,即使在稳态情况下,脉宽调速系统的转矩和转速也都 是脉动的。所谓稳态,是指电动机的平均电磁转矩与负载转矩相平衡的状态,机械特性是平 均转速与平均转矩电流)的关系。在中、小容量的脉宽调速系统中,IGBT已经得到普遍 的应用,其开关频率一般在10kHz左右,这时,最大电流脉动量在额定电流的5%以下,转 速脉动量不到额定空载转速的万分之一,可以忽略不计。 采用不同形式的PWM变换器,系统的机械特性也不一样。对于带制动电流通路的不可 逆电路和双极式控制的可逆电路,电流的方向是可逆的,无论是重截还是轻载,电流波形都 是连续的,因而机械特性关系式比较简单,下面就分析这种情况。 对于带制动电流通路的不可逆电路见图1-17),电压平衡方程式分两个阶段 U,=Ria+L+E 0≤t<t) 1-20) 0=Rig+L+E on≤t<T) 1-21) 式中的R、L分别为电枢电路的电阻和电感。 对于双极式控制的可逆电路见图1-18),只是将式Q-21)中电源电压由0改为 -U,其他均不变,即 U=R+L能+E 0≤t<tm) 1-22) -U,=Ria+L+E m≤t<T) 1-23) 按电压方程求一个周期内的平均值,即可导出机械特性方程式。无论是上述哪一种情 况,电枢两端在 个周期内的平均电压都是U。=YU,只是y与占空比ρ的关系不同,分别 为式1-17)和式1-19)。平均电流和转矩分别用【:和T.表示,平均转速n=EC. 而电枢电感压降L的平均值在稳态时应为零。于是,无论是上述那一组电压方程,其平 均值方程都可写成 YU,=RIa+E=RIa+C.m 4-24) 则机械特性方程式为 n-7g是1=0-是1 1-25) 或用转矩表示, -兴-品=w是 1-26) 式中,C。一电机在额定磁通下的转矩系数,C。=KDx! 理想空续转速,与电压系数了成正比,%光

17 图1一20所示为第一、二象限的机械特性,它适用于带制动作用的不可逆电路,双极式 控制可逆电路的机械特性与此相仿,只是扩展到 第三、四象限了对于电动机在同一方向旋转时 电流不能反向的电路,轻载时会出现电流断续现 象,把平均电压抬高,在理想空载时,【=0, 0.75 -y=0.75 理想空截转速会翘到mo,=U,C。.] 0.5m 0,25os y-0.5 1.3.3PWM控制与变换器的数学模型 -0.25 无论哪一种PWM变换器电路,其驱动电压 -4,- 都由PWM控制器发出,PWM控制器可以是模 图1-20脉宽调速系统的机械特 拟式的,也可以是数字式的,都已在电力电子 性。电流连续时) 技术”课程中介绍。图1-21所示为PWM控 制器和变换器的框图】 PWM控制与变换器的动态数学模型和晶闸 管触发与整流装置基木一致。按照上述对PWM 1-21PWM控制器与变换器的图 变换器工作原理和被形的分析,不看出,当一WM安出的直电 Ug一PWM径 制器输出到主电席开关器件的孤动电田 望制电压U.改变时,PWM变换器输出平均电 U。一PWM控制器的控制电丙 压U,按线性规律变化,但其响应会有延迟,最 大的时延是一个开关周期T。因此,PWM控制与变换器 简称PWM装置)也可以看成是 个滞后环节,其传递函数可以写成 w.)=:=K,e 1-27) 式中K,一PWM装置的放大系数: -PWM装置的延迟时间,T,≤T。 由于PWM装置的数学模型与品闸管装置一致,在控制系统中的作用也一样,因此W。), K。和T,都采用同样的符号。 当开关频率为10kHz时,T=0.1ms,在一般的电力拖动自动控制系统中,时间常数这 么小的滞后环节可以近似看成是一个一阶惯性环节,因此 1-28) 与晶闸管装置传递函数完全一致。但须注意,式1-28)是近似的传递函数,实际上 PWM变换器不是一个线性环节,而是具有继电特性的非线性环节。继电控制系统在一定条 件下会产生自激振满,这是采用线性控制理论的传递函数不能分析出来的。如果在实际系统 中遇到这类问题,简单的解决办法是改变调节器或控制器的结构和参数,如果这样做不能奏 效,可以在系统某一处施加高频的周期信号,人为地造成高频强制振荡,抑制系统中的自激 振荡,并使继电环节的特性线性化。] 1,3,4电能回馈与泵升电压的限制 图1-22所示是桥式可逆直流脉宽调速系统主电路的原理图GBT的吸收电路略去未