
第二部分信号的检测 广东工业大学机电工程学院 线性系统 定常线性系统:系统输入x()和输出y()间的关系可以 用常系数线性微分方程来描述: y(t)tay(t)+ay(t)+ay(t)(t)b(t)+bx(t)+b(t) 般在工程中使用的测试装置都是线性系统。 线性系统性质: a)叠加性 系统对各输入之和的输出等于各单个输入的输出之和 即 若 x1(t)→y1(t),x2()→y2(t) 则 x1()±x2()→y1(t)±y2(t)
第二部分 信号的检测 广东工业大学机电工程学院 定常线性系统:系统输入x(t)和输出y(t)间的关系可以 用常系数线性微分方程来描述: 线性系统 一般在工程中使用的测试装置都是线性系统。 线性系统性质: a)叠加性 系统对各输入之和的输出等于各单个输入的输出之和 ,即 若 x1(t) → y1(t),x2(t) → y2(t) 则 x1(t) ±x2(t) → y1(t) ±y2(t)
第二部分信号的检测 广东工业大学机电工程学院 b)比例性 常数倍输入所得的输出等于原输入所得输出的常数 倍,即 若 x(t) →y(t) 则 kx(t)→ky(t) c)微分性 系统对原输入信号的微分等于原输出信号的微分,即 若 x(t)→y(t) 则 x'()→y'(t) d)积分性 当初始条件为零时,系统对原输入信号的积分等于原 输出信号的积分,即 若 x(t) ·y(t) ∫x(t)dt→∫y(t)dt
第二部分 信号的检测 广东工业大学机电工程学院 b)比例性 常数倍输入所得的输出等于原输入所得输出的常数 倍,即: 若 x(t) → y(t) 则 kx(t) → ky(t) c)微分性 系统对原输入信号的微分等于原输出信号的微分,即 若 x(t) → y(t) 则 x'(t) → y'(t) d)积分性 当初始条件为零时,系统对原输入信号的积分等于原 输出信号的积分,即 若 x(t) → y(t) 则 ∫x(t)dt → ∫y(t)dt

第二部分信号的检测 广东工业大学机电工程学院 e)频率保持性 若系统的输入为某一频率的谐波信号,则系统的稳态输 出将为同一频率的谐波信号,即 若 x(t)=Acos(ωt什Φx) 则 y(t)=Bcos(ot+Φy) 线性系统的这些主要特性,特别是 符合叠加原理和频率保持性,在测量工 作中具有重要作用
第二部分 信号的检测 广东工业大学机电工程学院 e)频率保持性 若系统的输入为某一频率的谐波信号,则系统的稳态输 出将为同一频率的谐波信号,即 若 x(t)=Acos( ωt+ φx) 则 y(t)=Bcos( ωt+ φy) 线性系统的这些主要特性,特别是 符合叠加原理和频率保持性,在测量工 作中具有重要作用

第二部分信号的检测 广东工业大学机电工程学院 2.1.2测试系统静态特性 静态测量:测量时,测试装置的输入、输出信号不随时间而 变化 静态特性:静态测量时,测试装置表现出的特性 a)灵敏度 当测试装置的输入x有一增量△x,引起输出y发生相应 的变化△y时,则定义: S=△y/△x y A
第二部分 信号的检测 广东工业大学机电工程学院 静态测量:测量时,测试装置的输入、输出信号不随时间而 变化 静态特性:静态测量时,测试装置表现出的特性 2.1.2 测试系统静态特性 a)灵敏度 当测试装置的输入 x有一增量△ x,引起输出 y发生相应 的变化△ y时,则定义: S= △y/ △ x
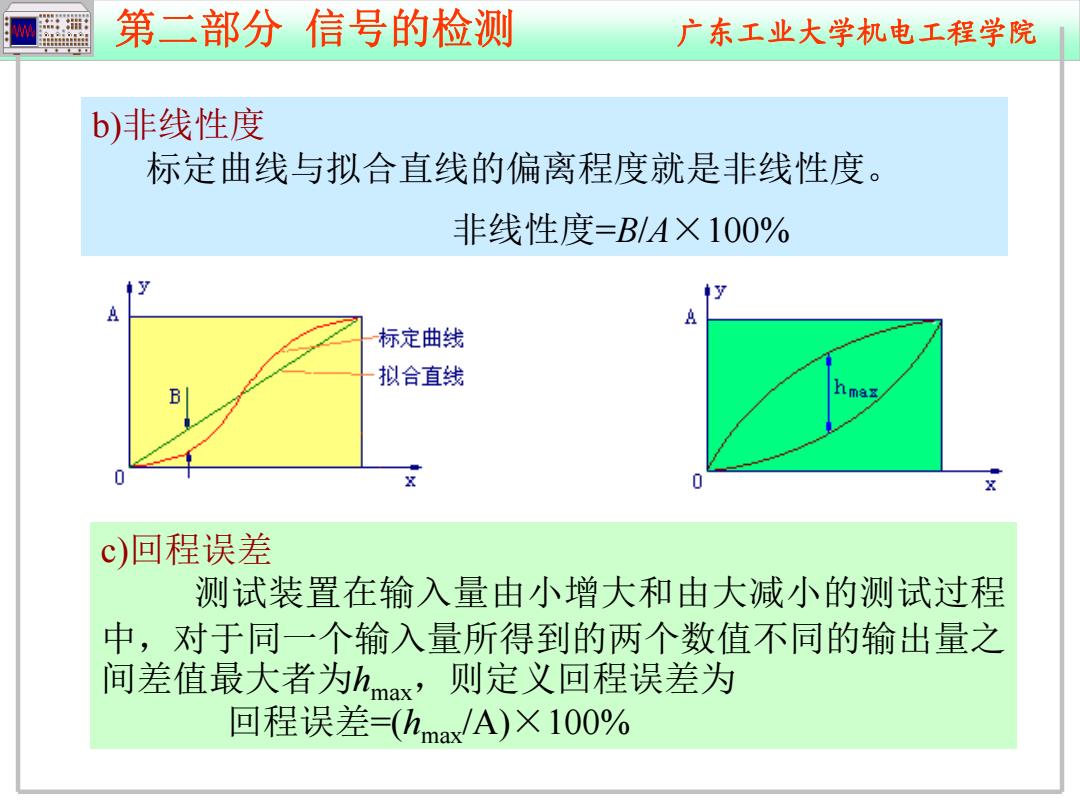
第二部分信号的检测 广东工业大学机电工程学院 b)非线性度 标定曲线与拟合直线的偏离程度就是非线性度。 非线性度=B/A×100% 标定曲线 拟合直线 c)回程误差 测试装置在输入量由小增大和由大减小的测试过程 中,对于同一个输入量所得到的两个数值不同的输出量之 间差值最大者为hmax,则定义回程误差为 回程误差=(hmax/A)×100%
第二部分 信号的检测 广东工业大学机电工程学院 b)非线性度 标定曲线与拟合直线的偏离程度就是非线性度。 非线性度 =B /A ×100% c)回程误差 测试装置在输入量由小增大和由大减小的测试过程 中,对于同一个输入量所得到的两个数值不同的输出量之 间差值最大者为 hmax,则定义回程误差为 回程误差=( hmax/A) ×100%