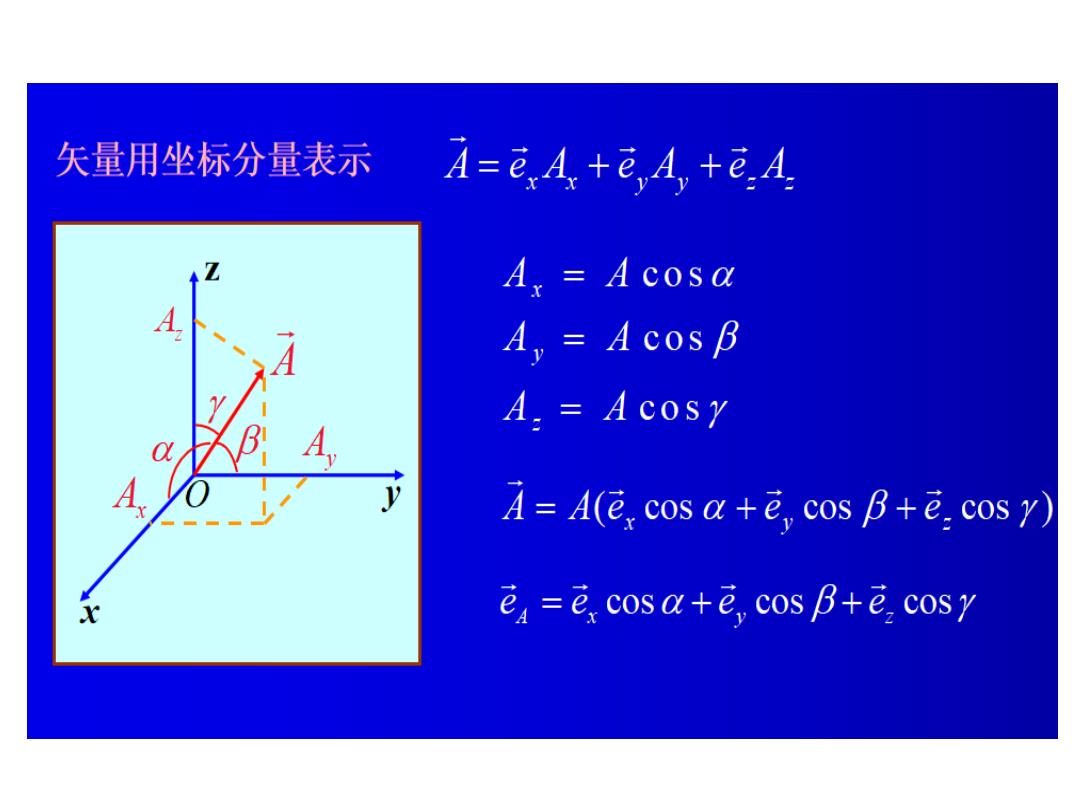
矢量用坐标分量表示 A=e,A+@,4,+e.A. A,Acosa A,Acos B A.=Acosy A=A(e,cos a+e,cos B+e.cosy) e,=e,cosa+e,cos B+e cosy
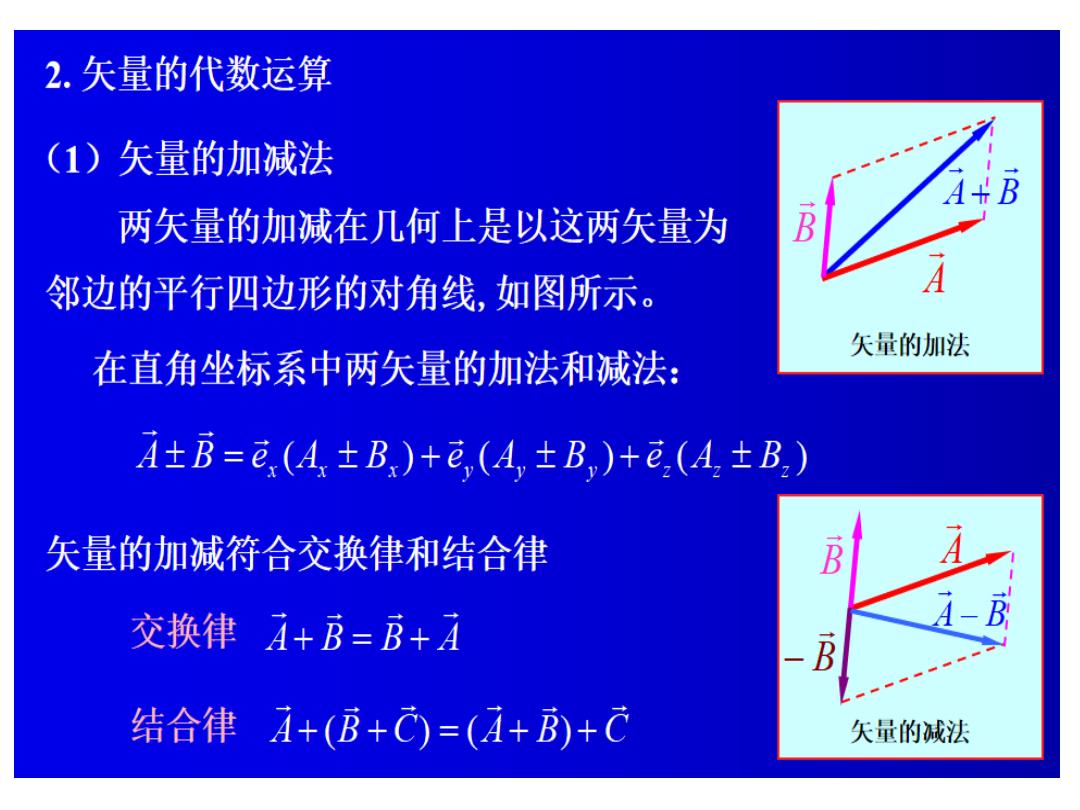
2.矢量的代数运算 (1)矢量的加减法 两矢量的加减在几何上是以这两矢量为 邻边的平行四边形的对角线,如图所示。 矢量的加法 在直角坐标系中两矢量的加法和减法: A±B=e(A±B)+e,(A,±B,+e(A±B.) 矢量的加减符合交换律和结合律 B 交换律A+B=B+ 1- 结合律A+(B+C)=(A+)+C 矢量的减法

(2)标量乘矢量 kA=ekA,+e,kA,+e.kA. (3)矢量的标积(点积) A 4.B=ABCOS0=A B,+AB,+A B 矢量A与B的夹角 AB=B,A—矢量的标积符合交换律 4L8→AB=0 A/B→AB=AB e,@,=ey'@.=e.@=0 e,e,=e,8,=8.'2.=1

(4)矢量的矢积(叉积) Ax B=eABsin 0 用坐标分量表示为 AxB=@(A,B.-AB)+(A.B:-A,B:)+e.(A,B,-A,B.) 写成行列式形式为 e e, AxB= A AxB A B By B AB sin 6 A×B=-BxA 6 A 若4⊥B,则A×B=AB 矢旺与B的叉积 若A/B,则Ax=0

第二章平面电磁波 麦克斯韦方程的演变 如何分析媒质中的电磁特性 第二章 如何分析有界电磁问题 平面电磁波 电磁学中的能量守恒 电磁场的产生、存在、分布 电磁场的传播 场 从时间和空间的维度去认知、研究 波 分析: 第三章:辅助函数; 第四章:电磁定理和原理; 第九章:近似解析方法; 第十章:矩量法; 第十一章:时域有限差分法;第十二章:有限元法 应用: 第五章:电磁辐射; 第六章:电磁散射; 第七章:导波理论; 第八章:谐振腔;
第二章 平面电磁波 麦克斯韦方程的演变 如何分析媒质中的电磁特性 如何分析有界电磁问题 电磁学中的能量守恒 第二章 平面电磁波 电磁场的产生、存在、分布 电磁场的传播 场 波 分析: 应用: 第三章:辅助函数; 第四章:电磁定理和原理; 第九章:近似解析方法; 第十章:矩量法; 第十一章:时域有限差分法; 第十二章:有限元法 第五章:电磁辐射; 第六章:电磁散射; 第七章:导波理论; 第八章:谐振腔; 从时间和空间的维度去认知、研究