
药剂学实验讲义
药 剂 学 实 验 讲 义

实验一、均匀设计在药学中的应用简介 一、方法的提出 1、原因: ①全面实验次数太多,有S个因素,每个因素取q个水平,实验次数为N=rq,例如5 个因素有3个水平,全面实验次数为35=243。 ②实验设计中一些不妥的做法:实验次数越多越可靠,实际上容易增加实验误差, 或产生系统误差:实验范围太小可能得出错误的结论。 2、常用名词: 指标:Target,因素:Factor,水平:Level。 3、原理: 正交设计:均匀分散,整齐可比。N=rq。 均匀设计:均匀分散。N=rq。 二、均匀设计表和使用表 1、均匀设计表 挑选实验点的原则: ()、各因素所取的水平数相等,每个因素的一个水平各做一次试验,共做q次试验 (2)、使试验点分布最均匀 (3)、最多允许所谓因素数S=q一1,但q只有为素数时才能达到: ()、当q为偶数时,利用比q大1的奇数表,即qp-1,p为奇数,划去最后一行即得。 U(uniform)一均匀表 q一因素所取水平数 N-试验数,N=q 最多可安排的因素数,S=q一1 表1均匀设计表U5(54) 表.2U5(54)使用表 1234 因素数 列号 23 2 1,2 1 3 1,2,4 4 2 1,2,3,4 2 5 5 5
实验一、均匀设计在药学中的应用简介 一、方法的提出 1、原因: ①全面实验次数太多,有S个因素,每个因素取q个水平,实验次数为N=rqs,例如5 个因素有3个水平,全面实验次数为3 5=243。 ②实验设计中一些不妥的做法:实验次数越多越可靠,实际上容易增加实验误差, 或产生系统误差;实验范围太小可能得出错误的结论。 2、常用名词: 指标:Target,因素:Factor,水平:Level。 3、原理: 正交设计:均匀分散,整齐可比。N=rq2。 均匀设计:均匀分散。N=rq。 二、均匀设计表和使用表 1、均匀设计表 挑选实验点的原则: ⑴、各因素所取的水平数相等,每个因素的一个水平各做一次试验,共做q次试验; ⑵、使试验点分布最均匀 ⑶、最多允许所谓因素数S=q-1,但q只有为素数时才能达到; ⑷、当q为偶数时,利用比q大1的奇数表,即q=p-1,p为奇数,划去最后一行即得。 U(uniform)-均匀表 q-因素所取水平数 N-试验数,N=q 最多可安排的因素数,S=q-1 表1均匀设计表U5(5 4) 表.2 U5(5 4)使用表 1 2 3 4 1 2 3 4 5 1 2 3 4 2 4 1 3 3 1 4 2 4 3 2 1 5 5 5 5 因素数 列 号 2 3 4 1,2 1,2,4 1,2,3,4
三、使用方法 1、步骤:①确定因素数。②确定水平数。q≥2s。③排因素水平表,拟水平。④排 实验表。⑤每个实验最好重复几次。⑥数据处理,拟合方程,分析。 2、说明:①水平数为偶数取比该水平数大1的奇数表,然后划去最后一行作为均匀 设计表。②所选因素数少于均匀设计表中最多可安排的因素数,按照均匀设计使用表来选 择哪几列安排实验。③如果某因素的取值范围比较窄,可采用拟水平法,即将同一水平连 续使用多次。 3、举例: 例1.HP一2农药增效剂的合成,有四个因素,取值范围如下,每个因素九个水平,构 成因素水平表,选用U。(9)均匀表,由于因素数4少于8,根据U。(9)使用表应选1,2, 3,5列,构成试验设计表。 A:正溴辛烷/尼内酰胺(mol/mol) 1.0-1.8 B:KOH/己内酰胺(mol/mol) 15-3.1 C:催化剂用量(g) 0.5-2.1 D:反应时间(h) 8-16 表1因素水平表 3 4 5 6 7 8 9 A 1.01.11.21.31.41.51.61.71.8 B 1.51.71.92.12.32.52.72.93.1 0.50.70.91.11.31.51.71.92.1 D 8 910111213141516 表2试验设计表 试 反应条件(列号) 指标(收率) 相对百分 验 B D Y(试验值)Ye(计算) 误差(%) 1(1.0)2(1.7)41.1)7(14) 0.5700 0.5733 -0.57 0.5303 0.5185 202 6 3 3 0.7080 0.7030 0.79 8 7 0.6360 0.648 -2.24 1 2 P 0.6200 0.6770 -10.09 3 6 6 0.6720 0.6227 8.64 5 0.8640 0.8077 9.87 > 5 2 0.7050 0.7330 -8.24 9 9 9 0.6910 0.6910 0.00
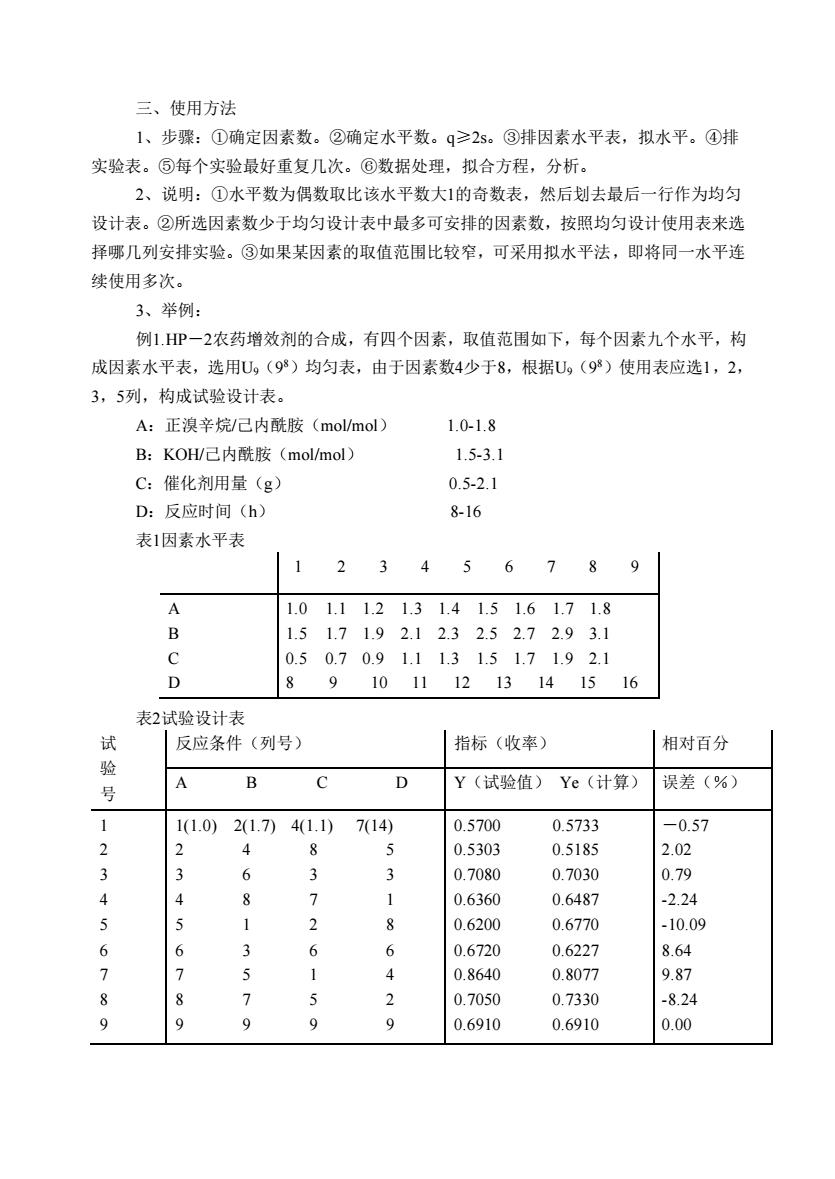
三、使用方法 1、步骤:①确定因素数。②确定水平数。q≥2s。③排因素水平表,拟水平。④排 实验表。⑤每个实验最好重复几次。⑥数据处理,拟合方程,分析。 2、说明:①水平数为偶数取比该水平数大1的奇数表,然后划去最后一行作为均匀 设计表。②所选因素数少于均匀设计表中最多可安排的因素数,按照均匀设计使用表来选 择哪几列安排实验。③如果某因素的取值范围比较窄,可采用拟水平法,即将同一水平连 续使用多次。 3、举例: 例1.HP-2农药增效剂的合成,有四个因素,取值范围如下,每个因素九个水平,构 成因素水平表,选用U9(9 8)均匀表,由于因素数4少于8,根据U9(9 8)使用表应选1,2, 3,5列,构成试验设计表。 A:正溴辛烷/己内酰胺(mol/mol) 1.0-1.8 B:KOH/己内酰胺(mol/mol) 1.5-3.1 C:催化剂用量(g) 0.5-2.1 D:反应时间(h) 8-16 表1因素水平表 1 2 3 4 5 6 7 8 9 A B C D 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.5 1.7 1.9 2.1 2.3 2.5 2.7 2.9 3.1 0.5 0.7 0.9 1.1 1.3 1.5 1.7 1.9 2.1 8 9 10 11 12 13 14 15 16 表2试验设计表 试 验 号 反应条件(列号) 指标(收率) 相对百分 A B C D Y(试验值) Ye(计算) 误差(%) 1 2 3 4 5 6 7 8 9 1(1.0) 2(1.7) 4(1.1) 7(14) 2 4 8 5 3 6 3 3 4 8 7 1 5 1 2 8 6 3 6 6 7 5 1 4 8 7 5 2 9 9 9 9 0.5700 0.5733 0.5303 0.5185 0.7080 0.7030 0.6360 0.6487 0.6200 0.6770 0.6720 0.6227 0.8640 0.8077 0.7050 0.7330 0.6910 0.6910 -0.57 2.02 0.79 -2.24 -10.09 8.64 9.87 -8.24 0.00

四、试验数据的处理 1、计算回归方程:由计算机对试验结果进行计算及处理得回归方程。 例1、以A,B,C,D四个因素为自变量,指标Y为应变量,水平q为样本数,首先计 算各因素之间以及各因素与指标间的单相关系数,见表,用以考察各因素之间的相关性, 根据多元线性回归计算的要求,各因素之间应相互独立,至少应不相关,两个十分相关的 因素不能同时进入回归方程。 相关系数表 A 0 Y A 1.0000 0.5000 1.0000 0.1000 0.5000 0.10000 0 0.1000 -0.40000.10000 1.0000 06445 03448 04769 -02389 1.0000 Ye=0.1708A+0.0828B-0.1332C-0.0008D+0.4195 N=9R=0.9187F=5.4099s-0.0537 Fo144=4.11 2、回归方程的显著性检验 ①相关系数检验:利用相关系数临界值表。 ②F检验。 3、利用回归方程进行结果解释及工艺条件优化。 ①根据回归方程各项系数的大小与正负,可以考察各项因素对指标的影响大小与主 次,例如上述方程中催化剂(C)的系数为负,表明催化剂的用量增加收率反而降低,从 相关性及实际情况中均可反映出这点。此外,时间这一项的系数很小,而且为负,说明时 间的影响不大,延长反应时间使副反应增多收率反而下降。如反应时间为8与15h的收率 相差不大(63.6%,62.0%),因此可以选择一个较短的时间为固定的反应时间,如7h,然后 改变其他的条件以取得更好的收率。 ②根据回归方程预测试验结果。以优化工艺的条件,预测最佳的工艺条件。例如: 固定反应时间D=7h,选择配料比A=1.8,KOH用量B=3.3g,催化剂用量C=0.3g,预报
四、试验数据的处理 1、计算回归方程:由计算机对试验结果进行计算及处理得回归方程。 例1、以A,B,C,D四个因素为自变量,指标Y为应变量,水平q为样本数,首先计 算各因素之间以及各因素与指标间的单相关系数,见表,用以考察各因素之间的相关性, 根据多元线性回归计算的要求,各因素之间应相互独立,至少应不相关,两个十分相关的 因素不能同时进入回归方程。 相关系数表 A B C D Y A 1.0000 B 0.5000 1.0000 C 0.1000 0.5000 0.10000 D 0.1000 -0.4000 0.10000 1.0000 Y 0.6445 0.3448 0.4769 -0.2389 1.0000 Ye=0.1708A+0.0828B-0.1332C-0.0008D+0.4195 N=9 R=0.9187 F=5.4099 s=0.0537 F0.1,4,4=4.11 2、回归方程的显著性检验 ①相关系数检验:利用相关系数临界值表。 ②F检验。 3、利用回归方程进行结果解释及工艺条件优化。 ①根据回归方程各项系数的大小与正负,可以考察各项因素对指标的影响大小与主 次,例如上述方程中催化剂(C)的系数为负,表明催化剂的用量增加收率反而降低,从 相关性及实际情况中均可反映出这点。此外,时间这一项的系数很小,而且为负,说明时 间的影响不大,延长反应时间使副反应增多收率反而下降。如反应时间为8h与15h的收率 相差不大(63.6%,62.0%),因此可以选择一个较短的时间为固定的反应时间,如7h,然后 改变其他的条件以取得更好的收率。 ②根据回归方程预测试验结果。以优化工艺的条件,预测最佳的工艺条件。例如: 固定反应时间D=7h,选择配料比A=1.8,KOH用量B=3.3g,催化剂用量C=0.3g,预报

收率为Yc=95.456%,实际合成收率为93.2%,相对误差为2.3%,与预测结果十分接近, 比原来最高收率提高7.8%。将C=0.5g,A不变仍为1.8,B=3.1,预测收率为Ye=91.02% 实际合成收率为90.5% 4、试验值异常点的处理。 如果回归方程计算的指标值与试验值相差较大时,应进行认真分析或重做。 5、关于试验数据的预处理 自变量的数量级相差较大时可先对数据进行规格化、标准化、取对数、压缩等。 ①规格化 (Xi-Xmin)/(Xma-Xmin) 数据经规格化后,数值压缩在0一1之间。 ②标准化 Zi=(Xij-Xj)/Sj S,2=(X-X)21n-1)
收率为Ye=95.456%,实际合成收率为93.2%,相对误差为2.3%,与预测结果十分接近, 比原来最高收率提高7.8%。将C=0.5g,A不变仍为1.8,B=3.1,预测收率为Ye=91.02%, 实际合成收率为90.5%。 4、试验值异常点的处理。 如果回归方程计算的指标值与试验值相差较大时,应进行认真分析或重做。 5、关于试验数据的预处理 自变量的数量级相差较大时可先对数据进行规格化、标准化、取对数、压缩等。 ①规格化 Zi,j=(Xi,j-Xmin)/(Xmax-Xmin) 数据经规格化后,数值压缩在0-1之间。 ②标准化 Zi,j=(Xi,j-Xj)/Sj Sj 2=(Xi,j-Xj) 2 /(n-1)