
求得扫描线上每点的法向量后,在 每点处实际计算亮度,可以应用任何一 种光照明模型。 如果应用镜面反射,比起亮度插值法 会得到明显的改进,因为强光能更加真 实地得到反映。即使不应用镜面反射, 法向插值的结果也比亮度插值的结果好。 这是因为对每一点都使用法向量的近似 值,使得可以减少Mach带效应引起的问 题。 但另一方面,对每一点都要计算亮 度, 使得计算量大为增加
求得扫描线上每点的法向量后,在 每点处实际计算亮度,可以应用任何一 种光照明模型。 如果应用镜面反射,比起亮度插值法 会得到明显的改进,因为强光能更加真 实地得到反映。即使不应用镜面反射, 法向插值的结果也比亮度插值的结果好。 这是因为对每一点都使用法向量的近似 值,使得可以减少Mach带效应引起的问 题。但另一方面,对每一点都要计算亮 度,使得计算量大为增加

绘制多边形的步骤: (1) 计算多边形的单位法矢量。 (2) 计算多边形顶点的单位法向量。 (3) 在扫描线消隐算法中,对多边形 顶点的法向量进行双线性插值,计算出多 边形内部(扫描线上位于多边形内部)各 点的法向量。 双线性插值的方法如图所示,NA由N1,N2 线性插值得到:
绘制多边形的步骤: (1) 计算多边形的单位法矢量。 (2) 计算多边形顶点的单位法向量。 (3) 在扫描线消隐算法中,对多边形 顶点的法向量进行双线性插值,计算出多 边形内部(扫描线上位于多边形内部)各 点的法向量。 双线性插值的方法如图所示,NA由N1,N2 线性插值得到:
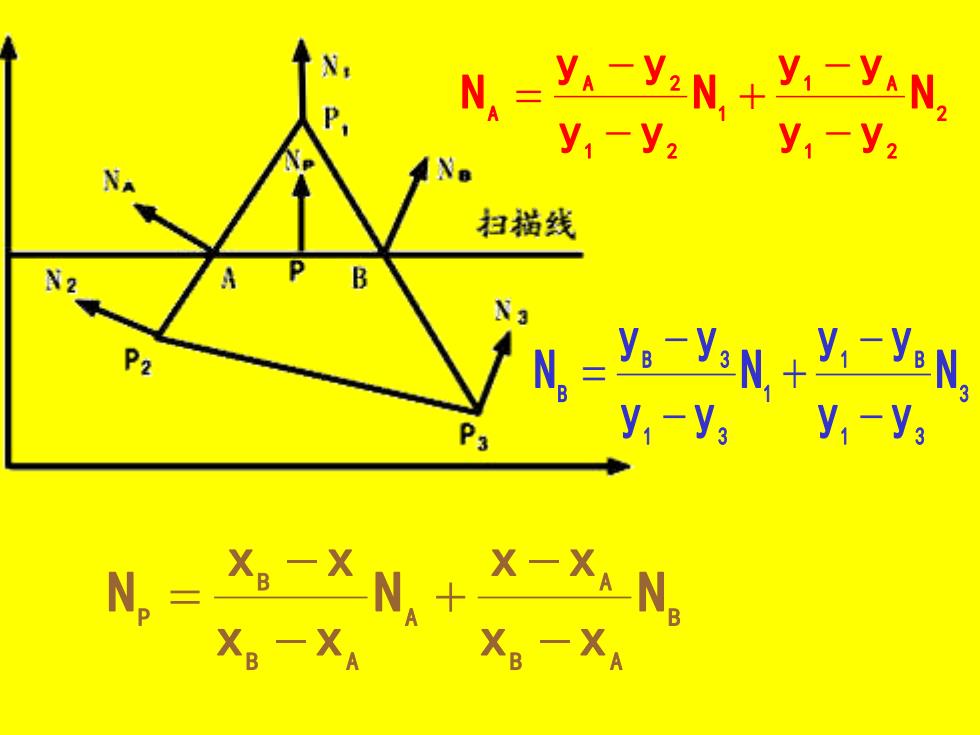
N.-Y.-Y.N+Y.-Y.N, y,-y2y,-y2 扫猫线 N2 B N-Y.-Y-N.+V.-YeN y,-y,y,-Va XXN X一XAN 一XA X。一X
2 1 2 1 A 1 1 2 A 2 A N y y y y N y y y y N − − + − − = 3 1 3 1 B 1 1 3 B 3 B N y y y y N y y y y N − − + − − = B B A A A B A B P N x x x x N x x x x N − − + − − =

(4) 利用光照明模型计算P点的颜色。 当扫描线y递增一个单位变为y+1时, NA,NB的增量分别为△NA,△NB,即 NAy:=NAy +A N Nox =Noy +A Ne △NA= (N-N,)△N=1 (N-N3 y1-y2 y,-y3 当x递增一个单位(P点沿扫描右移一个 单位)时,NP增量为△NP即 Npx1=N,x+△NAN,= (N-N) XB一XA
(4) 利用光照明模型计算P点的颜色。 当扫描线y递增一个单位变为y+1时, NA,NB的增量分别为△NA,△NB,即 NAy+1 = NAy +Δ NA NBy+1 = NBy +Δ NB ( N N ) y y 1 Δ N 1 2 1 2 A − − = ( N N ) y y 1 Δ N 1 3 1 3 B − − = NP ,x+1 = NP ,x +Δ N p ( N N ) x x 1 Δ N B A B A P − − = 当x递增一个单位(P点沿扫描右移一个 单位)时,NP增量为△NP即

Phong着色方法中,多边形上每一点需要 计算一次光照明模型,因而计算量远大于 Gouraud着色方法。但是Phong着色方法绘制 的图形更加真实,特别体现在如下两个场合 (考虑要绘制一个三角形)。 如果镜面反射指数n较大,三角形左下 角的顶点a(R与V的夹角)很小,而另两个顶 点的a很大,以光照明模型计算的结果是左下 角顶点的亮度非常大(高光点),另两个顶 点的亮度小。若采用Gouraud方法绘制,由于 它是对顶点的亮度进行插值,导致高光区域 不正常地扩散成很大一块区域
Phong着色方法中,多边形上每一点需要 计算一次光照明模型,因而计算量远大于 Gouraud着色方法。但是Phong着色方法绘制 的图形更加真实,特别体现在如下两个场合 (考虑要绘制一个三角形)。 如果镜面反射指数n较大,三角形左下 角的顶点a(R与V的夹角)很小,而另两个顶 点的a很大,以光照明模型计算的结果是左下 角顶点的亮度非常大(高光点),另两个顶 点的亮度小。若采用Gouraud方法绘制,由于 它是对顶点的亮度进行插值,导致高光区域 不正常地扩散成很大一块区域