
上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY Average Velocity of Gas Molecules Monatomic,ideal gas in equilibrium with its pressure and temperature 1-2 my=kT PV=nRT 3 The average energy,<E>,of the molecule is 2 3 Specific Internal Energy per mole: R 2 U=N<E> U=N 3 kT= 32 RT C-( 3-2 R
v kT 2 m 3 1 The average energy, <E>, of the molecule is kT 2 3 m 2 1 2 v R 2 3 ) T U ( RT 2 3 kT 2 3 U U V A A C N N E Specific Internal Energy per mole:

上浒充通大警 SHANGHAI JIAO TONG UNIVERSITY Average Velocity of Gas Molecules The rate of motion of molecules in O2 at macroscopic equilibrium 2=3kT/m=23.4×104m2/S2 v=483m/S NAIIAO TONG UNIV R=8.314472(15)JK-1mo-1 K=R/NA=1.38X10-23 m=32X10-kg/6.02X1023mo1
K=R/NA=1.38X10-23 R = 8.314472(15) J·K−1·mol−1 O2 m = 32X10-3 kg/6.02X1023mol-1

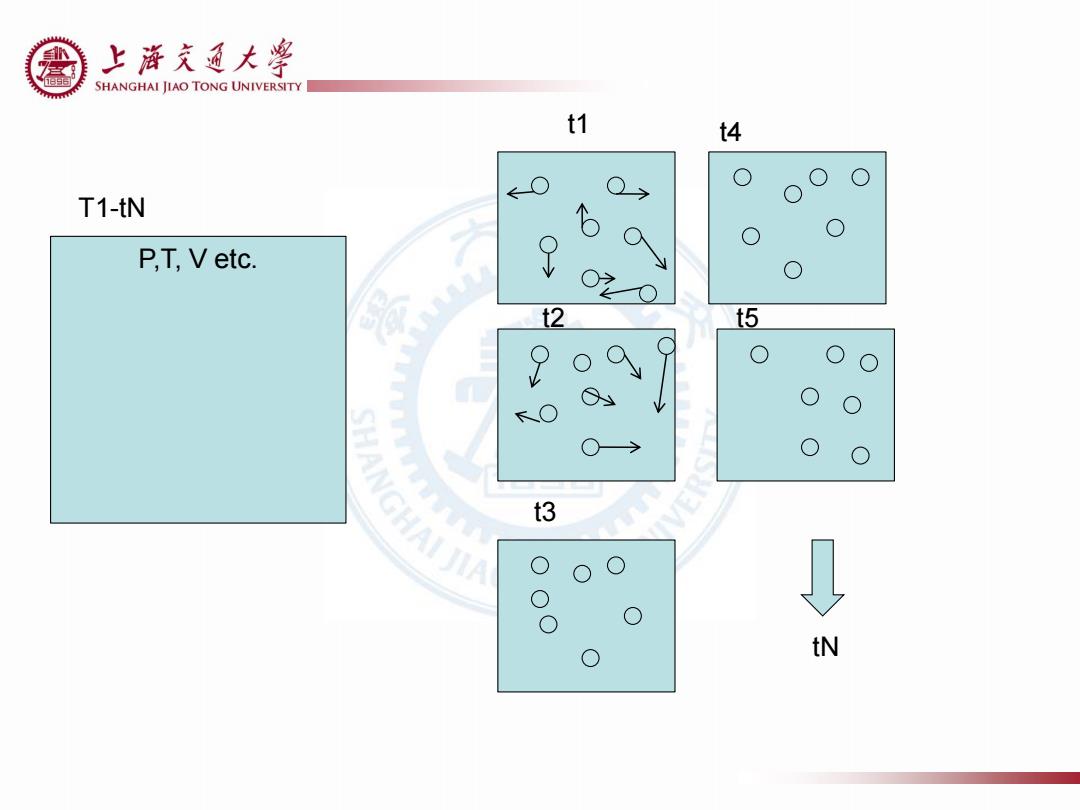
上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 10.2 Microstates and Macrostates ·宏观态 体系的状态由几个状态参数如温度、体积和内能来描述。 An isolated system at equilibrium at a given volume. ·微观态 需表征体系中所有粒子的状态,如所有分子的能量和速度。 Specify the position and velocity of all of the molecules in the system Macrostates:Characterized by a few state variables,such as T,P,internal energy Microstates:Characterize the state of all the particles in the system
10.2 Microstates and Macrostates Macrostates: Characterized by a few state variables, such as T, P, internal energy Microstates: Characterize the state of all the particles in the system
上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY t1 t4 T1-tN P.T,V etc. t5 SHANGHAUIA t3 Q o tN
P,T, V etc. t1 t2 t3 t4 t5 tN T1-tN

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 10.2 Microstates and Macrostates In order to compute the macroseopic average of a property .The property of each microstate .Which microstates the system can be in .The probability that the system will be in a given microstate The macroscopic pressure equals to the time average of the Macrostate: instantaneous pressure stating the total number of particles in each box yields Macroscopic pressure Microstate: each way of realizing a given macro distribution Instantaneous pressure Each macrostate may be realized by a number of microstates Time> Figure 10.2 Instantaneous gas pressure as a function of time.(The magnitude of the variation of instantaneous gas pressure is exag- gerated for emphasis.)
10.2 Microstates and Macrostates The macroscopic pressure equals to the time average of the instantaneous pressure