复单位:A、B、O不相邻(不在一条直线上) 平行四边形内摊到两个或两个以上结点构成复单位。 平面点阵的平移群 Tm=ma+nb m,n=0,±1,±2,±3.) 平面点阵也称平面格子。 在一个二维点阵中, 有多少个素单位? 有多少个复单位?
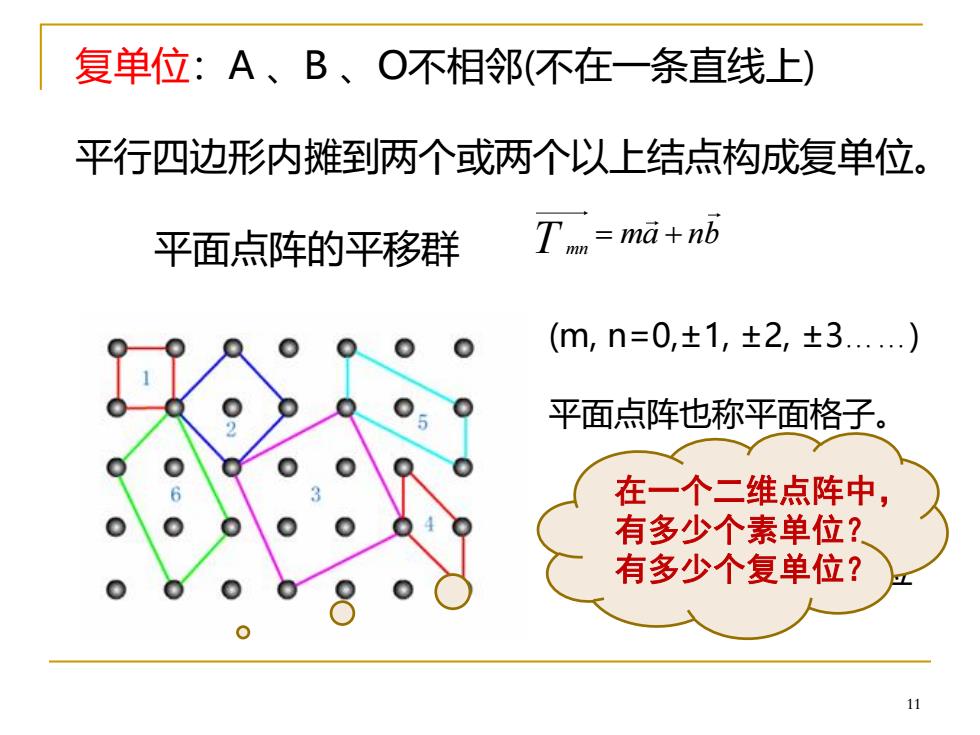
11 复单位:A 、B 、O不相邻(不在一条直线上) 平行四边形内摊到两个或两个以上结点构成复单位。 平面点阵的平移群 mn T = + ma nb (m, n=0,±1, ±2, ±3.) 平面点阵也称平面格子。 1,4 素单位 2,3,5,6 复单位 在一个二维点阵中, 有多少个素单位? 有多少个复单位?

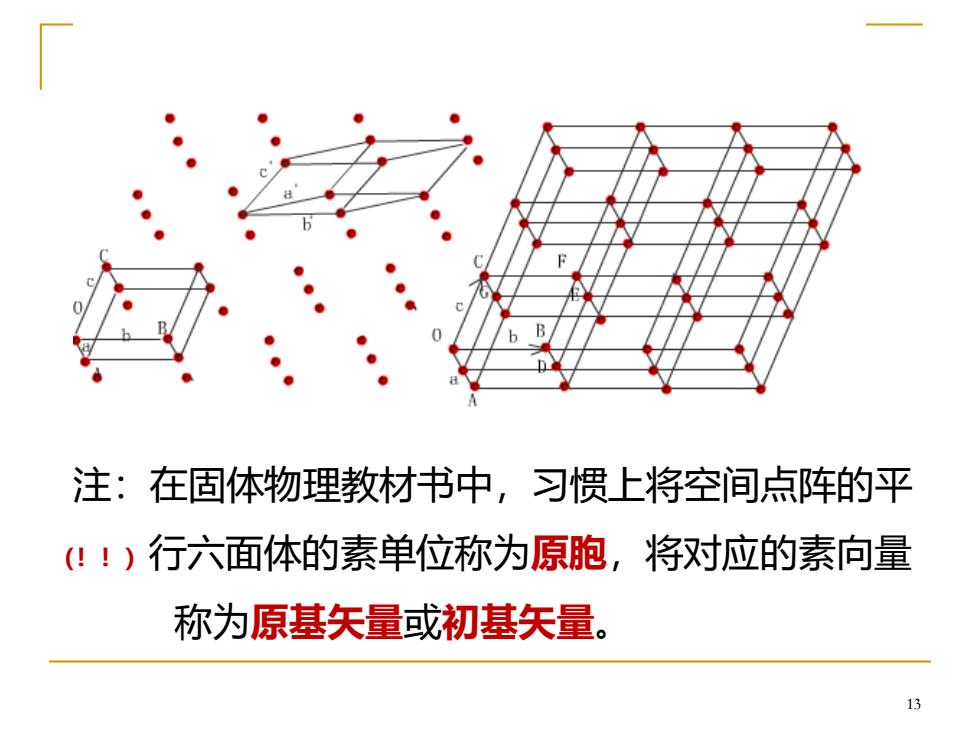
3、空间点阵 什么是空间点阵(三维点阵)? 一组平行等距的平面点阵构成的三维列阵。 O点与点A、B、C是最近邻的三个点,a、b、c 为素向量,三个素向量构成的平行六面体内只摊到 一个结点,称其为空间点阵的素单位。 空间点阵的平移群为: (m,n,p=0,±1,±2,±3.) Tmmp=ma+nb+pe 空间点阵也称为空间格子。 12
12 3、空间点阵 什么是空间点阵(三维点阵)? 一组平行等距的平面点阵构成的三维列阵。 O点与点A、B、C是最近邻的三个点, 为素向量,三个素向量构成的平行六面体内只摊到 一个结点,称其为空间点阵的素单位。 空间点阵的平移群为: (m, n, p=0,±1, ±2, ±3.) 空间点阵也称为空间格子。 a b c 、 、 mnp T = + + ma nb pc
注:在固体物理教材书中,习惯上将空间点阵的平 (!!)行六面体的素单位称为原胞,将对应的素向量 称为原基矢量或初基矢量。 13
13 注:在固体物理教材书中,习惯上将空间点阵的平 (!!)行六面体的素单位称为原胞,将对应的素向量 称为原基矢量或初基矢量

结论归纳如下: 什么是点阵? 一组按连结其中任何两点的向量进行平移后 而能复原的点。 (几何/形象) 什么是平移群? 能使一个点阵复原的全部平移形成的一个平移 群。 (数学/抽象) 平移群的重要性质:属于某平移群(Tmp)的任何二向 量(T1、T2)之和或之差也属于该平移群。 (群的封闭性)
14 结论归纳如下: 什么是点阵? 一组按连结其中任何两点的向量进行平移后 而能复原的点。 (几何/形象) 什么是平移群? 能使一个点阵复原的全部平移形成的一个平移 群。 (数学/抽象) 平移群的重要性质: 属于某平移群(Tmnp)的任何二向 量(T1、T2 )之和或之差也属于该平移群。 (群的封闭性)

2.2十四种空间点阵形式 为了比较和研究点阵形式方便,一般情况只需 研究点阵中的一个空间格子中结点的分布方式就可以 了。 由于对同一空间点阵,划分空间格子的方式是 多种多样的。为使点阵和点阵中选取的格子之间具有 一一对应的关系,人们对在点阵中选择的单位平行六 面体格子作了一些规定。 *三条规定
15 2.2 十四种空间点阵形式 为了比较和研究点阵形式方便,一般情况只需 研究点阵中的一个空间格子中结点的分布方式就可以 了。 由于对同一空间点阵,划分空间格子的方式是 多种多样的。为使点阵和点阵中选取的格子之间具有 一一对应的关系,人们对在点阵中选择的单位平行六 面体格子作了一些规定。 ** 三条规定