
直线点阵可以由一组使点阵复原的素向量和复向量 来表示,称平移群。直线点阵的平移群可以写成: T=ma m的取值 (m=0,±1,±2,±3。.),它点阵的代 到多少? 点阵和平移群有如下的对应关系: (1)从点阵中某一点指向点阵中其它点的向量为平 移群所包括无遗。向量→表达式 (2)以点阵中任意点为起点时,平移群中的每一个向 量都指向点阵中的一个点。表达式→向量 6
6 直线点阵可以由一组使点阵复原的素向量和复向量 来表示,称平移群。直线点阵的平移群可以写成: (m=0,±1, ±2, ±3.),它是点阵的代数表达式。 点阵和平移群有如下的对应关系: (1) 从点阵中某一点指向点阵中其它点的向量为平 移群所包括无遗。向量→表达式 (2) 以点阵中任意点为起点时,平移群中的每一个向 量都指向点阵中的一个点。表达式→向量 m T = ma m的取值 到多少?
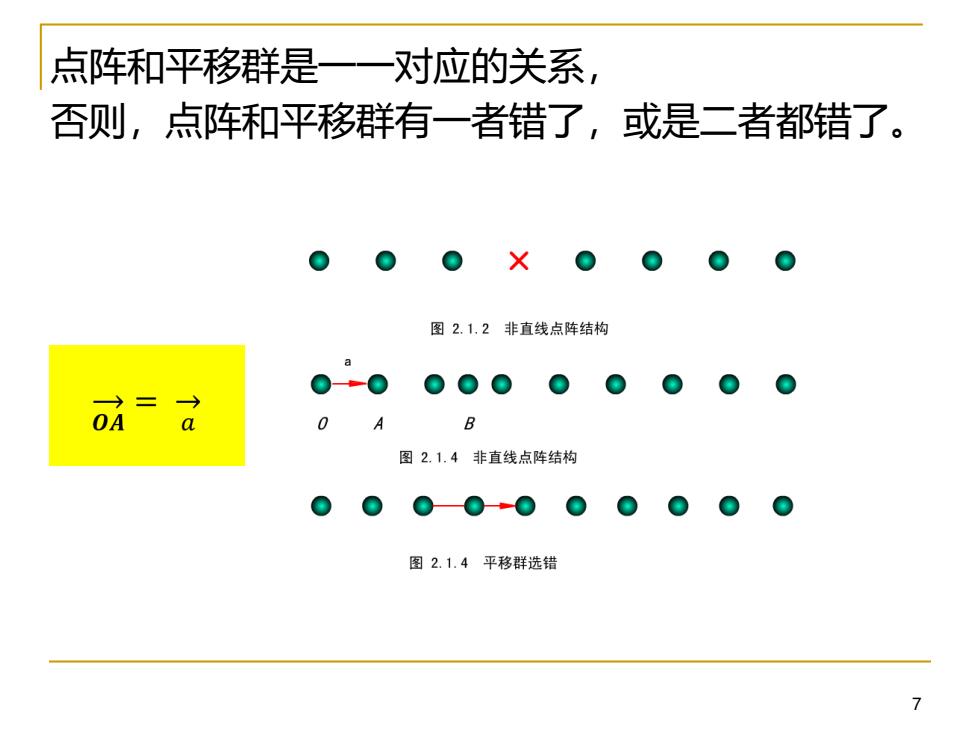
点阵和平移群是一一对应的关系, 否则,点阵和平移群有一者错了,或是二者都错了。 图2.1.2非直线点阵结构 OA a 0 A B 图2.1.4非直线点阵结构 0000 图2.1.4平移群选错
7 点阵和平移群是一一对应的关系, 否则,点阵和平移群有一者错了,或是二者都错了
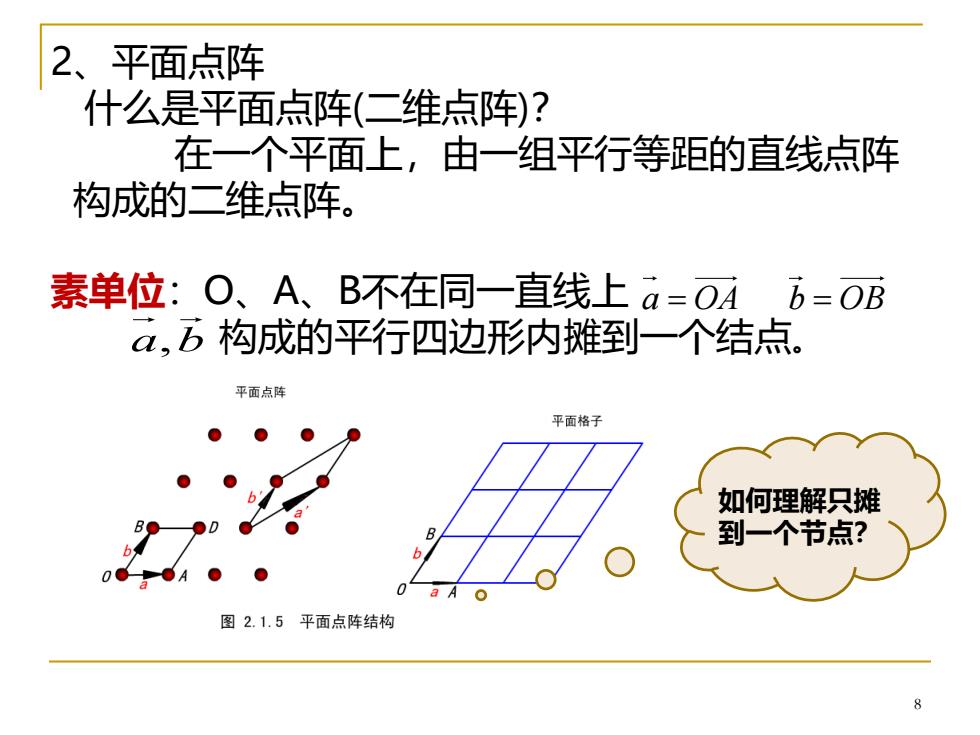
2、平面点阵 什么是平面点阵(二维点阵)? 在一个平面上,由一组平行等距的直线点阵 构成的二维点阵。 素单位:O、A、B不在同一直线上a=OA=OB a,五构成的平行四边形内摊到一个结点。 平面点阵 平面格子 如何理解只摊 到一个节点? 6 0 a A 图2.1.5平面点阵结构
8 2、平面点阵 什么是平面点阵(二维点阵)? 在一个平面上,由一组平行等距的直线点阵 构成的二维点阵。 素单位:O、A、B不在同一直线上 构成的平行四边形内摊到一个结点。 a OA = b OB = a b, 如何理解只摊 到一个节点?
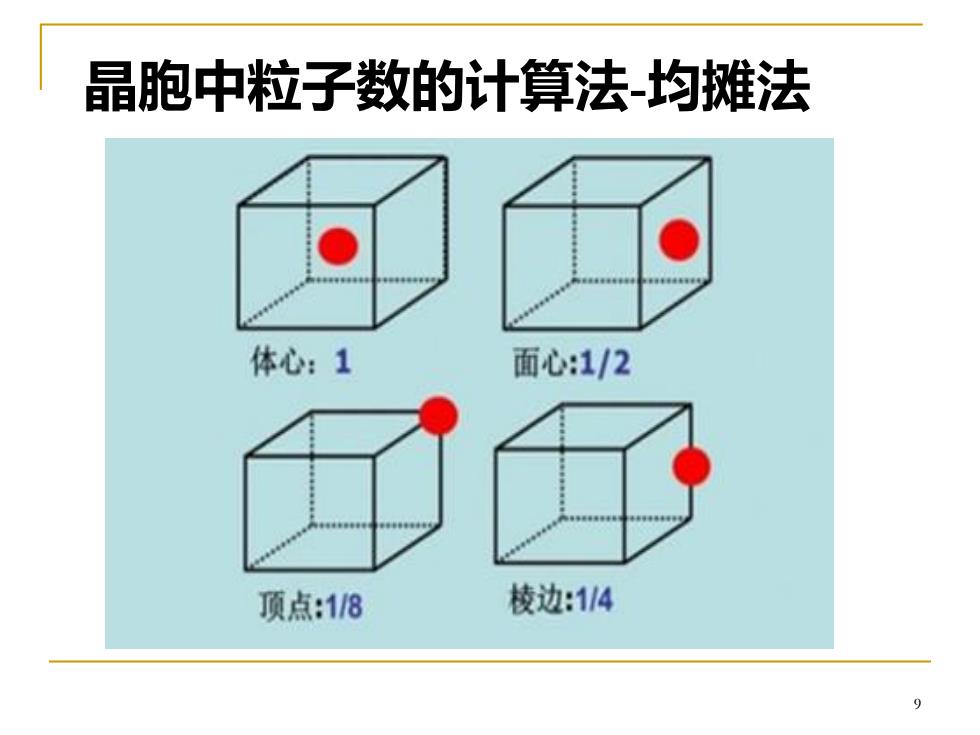
晶胞中粒子数的计算法-均摊法 体心:1 面心:1/2 顶点:1/8 棱边:1/4
晶胞中粒子数的计算法-均摊法 9
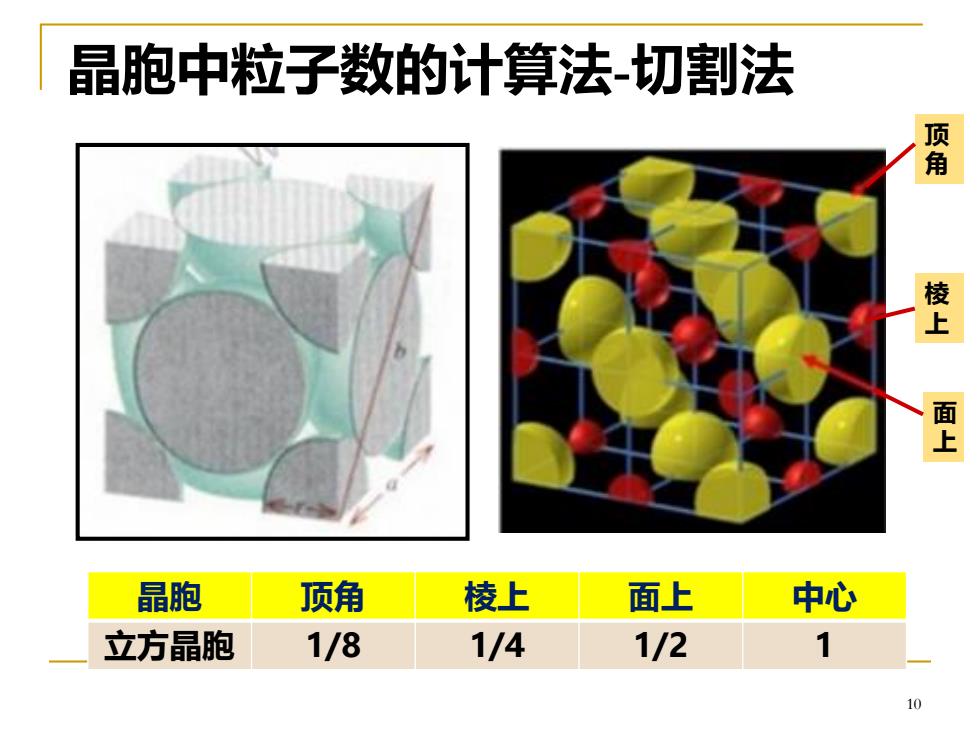
晶胞中粒子数的计算法切割法 檀 面 晶胞 顶角 棱上 面上 中心 立方晶胞 1/8 1/4 1/2 1
10 晶胞中粒子数的计算法-切割法 晶胞 顶角 棱上 面上 中心 立方晶胞 1/8 1/4 1/2 1 顶 角 棱 上 面 上