
间题6: 两个block的“边界”是什么? Corollary 5.9 Every two distinct blocks B1 and B2 in a nontrivial connected graph G have the following properties: (a)The blocks B1 and B2 are edge-disjoint. (b)The blocks B1 and B2 have at most one vertex in common. (c)If B1 and B2 have a vertex v in common,then v is a cut-vertex of G
Corollary 5.9 Every two distinct blocks B1 and B2 in a nontrivial connected graph G have the following properties: (a) The blocks B1 and B2 are edge-disjoint. (b) The blocks B1 and B2 have at most one vertex in common. (c) If B1 and B2 have a vertex v in common, then v is a cut-vertex of G

点连通度K(G) 最小点割集的势 请特别注意:极小点割集和最小点割集 Minimal和minimum
点连通度K(G) 请特别注意:极小点割集和最小点割集 Minimal和minimum 最小点割集的势

K-连通图 K(G)>=k 间题7: 从一个k连通图中删除k个点,剩下的图是否一 定不连通了? 问题8; Bl回ck和2-连通图是什么关系?
K-连通图 从一个k-连通图中删除k个点,剩下的图是否一 定不连通了? K(G)>=k

问题9: 边连通度是什么概念? 我们能够简称4边连通度图为4连通图吗?
Theorem 5.10 (K,)=n-1 定是两 证明: 个吗? 1, 显然,(Kn)≤n-1 2,令X是某个minimum边割集,将G分割为两个连通分量G1和G2 不失一般性,G1中含有k个点,G2中有n-k个点 XI k*(n-k) ∥G是完全图 k-1>=0,n-k-1>=0,所以: (k-1)n-k-1)=k(n-k)-(n-1)>=0 G1 G2 k(n-k)>=n-1 (Km)≥n-1 3,(Kn)=n-1
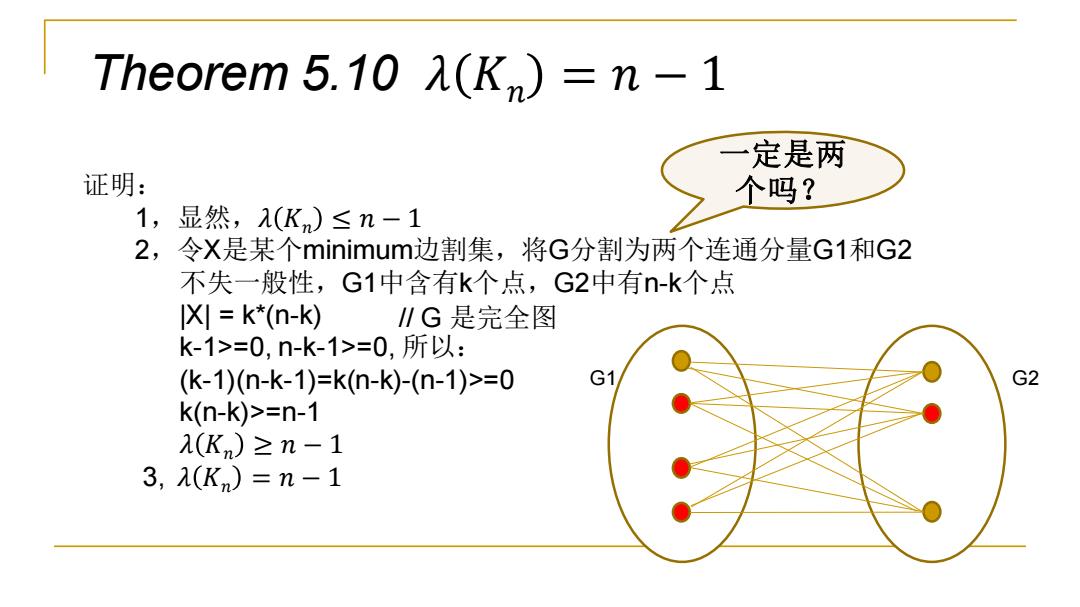
Theorem 5.10 𝜆 𝐾𝑛 = 𝑛 − 1 G1 G2 证明: 1,显然,𝜆 𝐾𝑛 ≤ 𝑛 − 1 2,令X是某个minimum边割集,将G分割为两个连通分量G1和G2 不失一般性,G1中含有k个点,G2中有n-k个点 |X| = k*(n-k) k-1>=0, n-k-1>=0, 所以: (k-1)(n-k-1)=k(n-k)-(n-1)>=0 k(n-k)>=n-1 𝜆 𝐾𝑛 ≥ 𝑛 − 1 3, 𝜆 𝐾𝑛 = 𝑛 − 1 一定是两 个吗? // G 是完全图