
计算机问题求解一论题3-11 -图旅行 2020年12月1日
计算机问题求解 – 论题3-11 - 图旅行 2020年12月1日
Konigsberg七桥问题 ·问题的抽象: ·用顶点表示对象-“地块” 这里看到的图建 模过程,应该被 ·用边表示对象之间的关系.“有桥相连” 深刻理解和记忆 ·原问题等价于:“右边的图中是否存在包: 行灯一 次的回路?” B
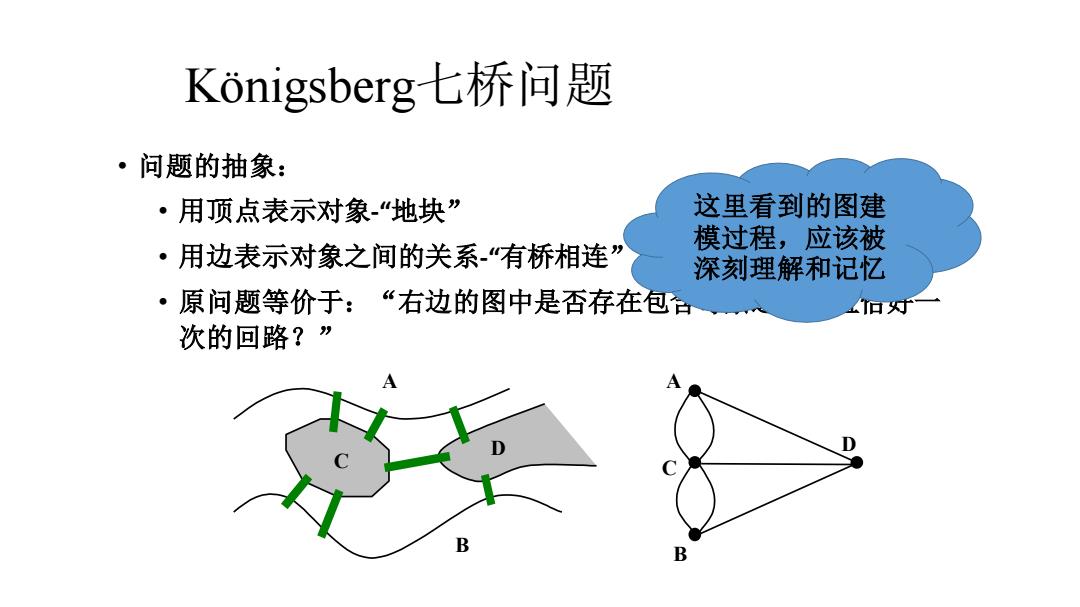
Königsberg七桥问题 • 问题的抽象: • 用顶点表示对象-“地块” • 用边表示对象之间的关系-“有桥相连” • 原问题等价于:“右边的图中是否存在包含每条边一次且恰好一 次的回路?” C D A B A C B D 这里看到的图建 模过程,应该被 深刻理解和记忆
一笔划”问题 问题1:如何为 一笔画问题进行 形式化描述?
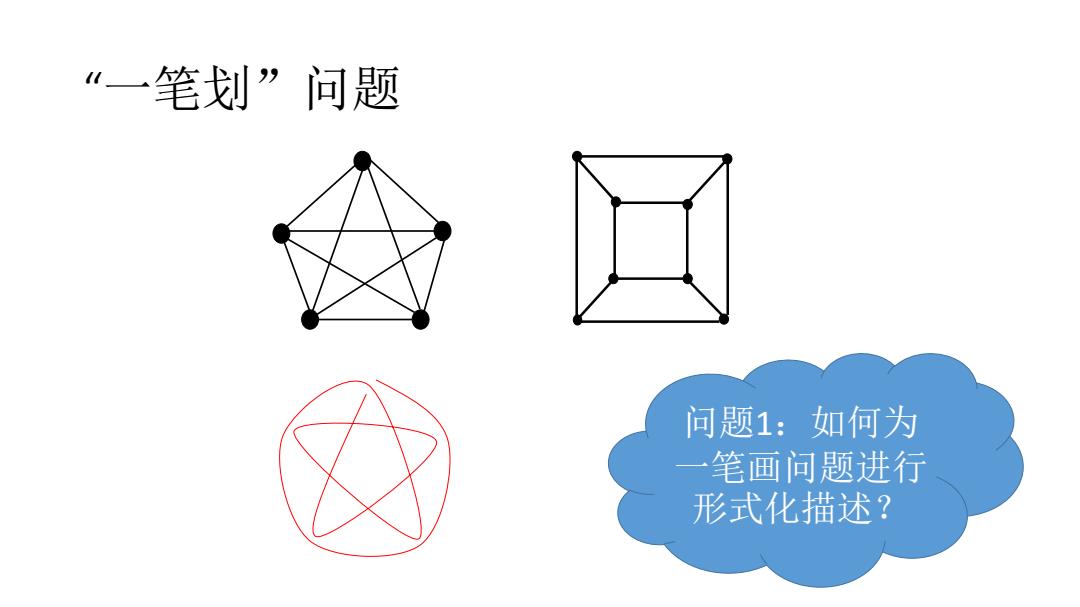
“一笔划”问题 问题1:如何为 一笔画问题进行 形式化描述?

欧拉通路和欧拉▣路 ·定义:包含图(无向图或有向图)中每条边的简单通路称为欧拉通 路。 注意:欧拉通路是简单通路(边不重复),但顶点可重复 ·定义:包含图中每条边的简单回如 ·如果图G中含欧拉回路,m 问题2:你能够想象 但没有欧拉回路,则G 欧拉是如何思考这 /备注:通常假设G是连 个问题的吗?
欧拉通路和欧拉回路 • 定义:包含图(无向图或有向图)中每条边的简单通路称为欧拉通 路。 注意:欧拉通路是简单通路(边不重复),但顶点可重复 • 定义:包含图中每条边的简单回路称为欧拉回路。 • 如果图G中含欧拉回路,则G称为欧拉图。如果图G中有欧拉通路, 但没有欧拉回路,则G称为半欧拉图。 //备注:通常假设G是连通的。 问题2:你能够想象 欧拉是如何思考这 个问题的吗?

欧拉图中的顶点度数 ·连通图G是欧拉图当且仅当G中每个顶点的度数均为偶数。 ·证明: →设C是G中的欧拉回路,则vEvG,d(y)必等于v在C上出现数的2倍(起 点与终点看成出现一次)。 可以证明: (1)G中所有的边可以分为若干边不相交的简单回路。 (2)这些回路可以串成一个欧拉回路
欧拉图中的顶点度数 • 连通图G是欧拉图 当且仅当 G中每个顶点的度数均为偶数。 • 证明: 设C是G中的欧拉回路,则vVG , d(v)必等于v在C上出现数的2倍(起 点与终点看成出现一次)。 可以证明: (1)G中所有的边可以分为若干边不相交的简单回路。 (2)这些回路可以串成一个欧拉回路