Whitney定理 Theorem 5.11 For every graph G, (G≤λ(G)≤6(G) 证明:1,平凡图和完全图是符合定理要求的:0,或者n-1 2,对非完全图,显然,(G)≤6(G)≤n-2 3,对非完全图,令X是某个最小边割集,X=(G)≤n-2。X集合将G分割为两个连通分量G1和G2 观察K(G)和1(G) G1 G2
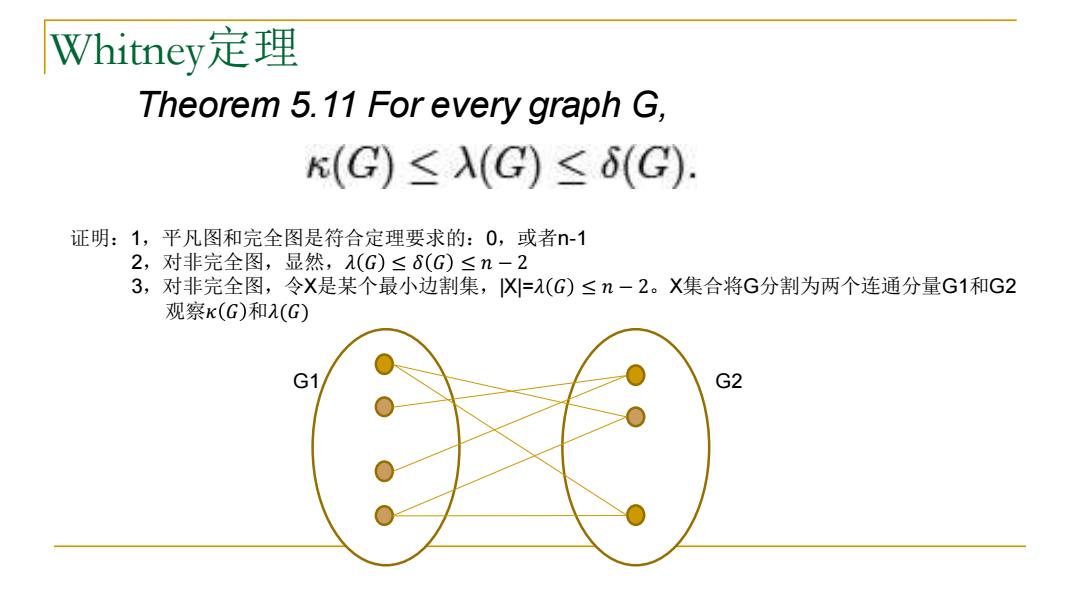
Whitney定理 Theorem 5.11 For every graph G, 证明:1,平凡图和完全图是符合定理要求的:0,或者n-1 2,对非完全图,显然,𝜆 𝐺 ≤ 𝛿 𝐺 ≤ 𝑛 − 2 3,对非完全图,令X是某个最小边割集,|X|=𝜆 𝐺 ≤ 𝑛 − 2。X集合将G分割为两个连通分量G1和G2 观察𝜅 𝐺 和𝜆(𝐺) G1 G2
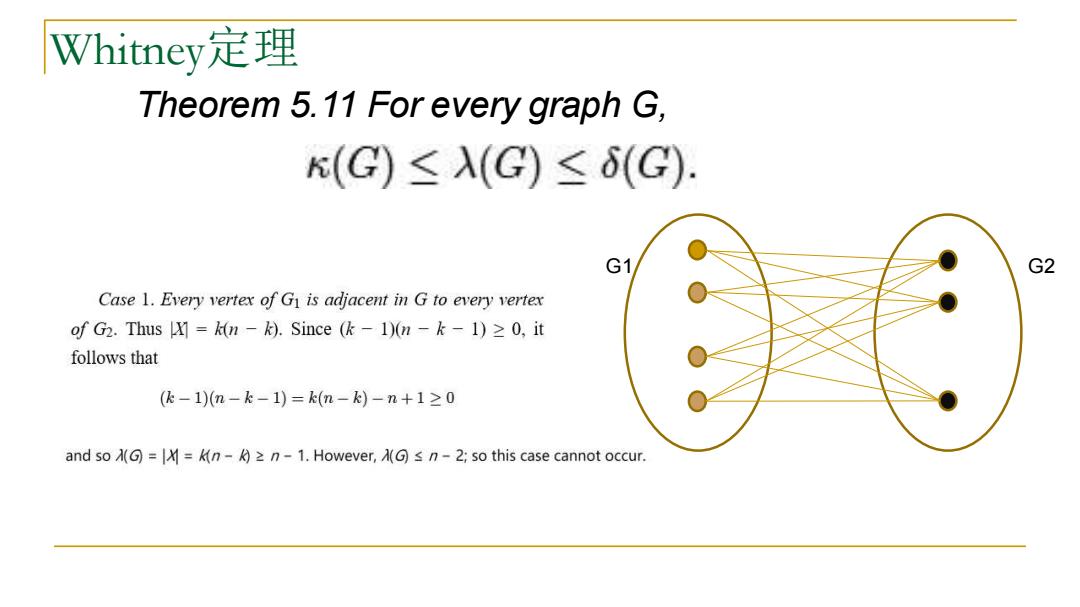
Whitney定理 Theorem 5.11 For every graph G, K(G)≤λ(G)≤6(G). G1 G2 Case 1.Every vertex of G is adjacent in G to every vertex ofG.Thus X=kn-).Since(k-1)n-k-1)≥0,it follows that (k-1)(n-k-1)=k(n-)-n+1≥0 and so (G)==n2n-1.However,A(G)s n-2;so this case cannot occur
Whitney定理 Theorem 5.11 For every graph G, G1 G2