
计算机问题求解一论题4-2 -置换群与拉格朗日定理 2021年3月3日
计算机问题求解 – 论题4-2 - 置换群与拉格朗日定理 2021年3月3日
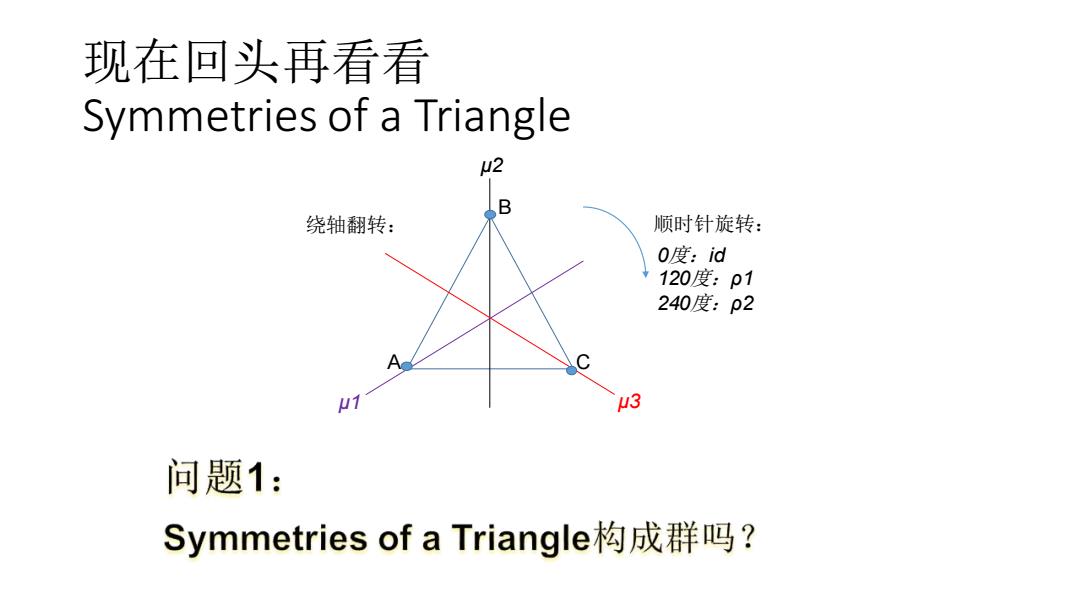
现在回头再看看 Symmetries of a Triangle u2 B 绕轴翻转: 顺时针旋转: 0度:id 120度:p1 240度:p2 1 u3 问题1: Symmetries of a Triangle构成群吗?
现在回头再看看 Symmetries of a Triangle A B C 0度:id 120度:ρ1 240度:ρ2 μ2 μ1 μ3 绕轴翻转: 顺时针旋转:

问题2: 任意非空集合上所有一一对应 的函数及函数复合运算一定能 构成一个群? Sn:n元素对称群 置换群:Sn的子群
Sn:n元素对称群 置换群:Sn的子群

关于置换的轮换表示 2345 6 42356/ =(243) 1g89)=12r66 12 2345
关于置换的轮换表示

置换复合运算示例 It is very easy to compute products of cycles.Suppose that σ=(1352) andT=(256).u=(1634) 0T三? 0L=? 123456 /123456 325461 614325
置换复合运算示例 ? ? 123456 325461 123456 614325