
2.回路矩阵B 一描述独立回路与支路的关联性质 支路b 独立回路 每一行对应一个独立回路, 每一列对应一条支路。 ()矩阵B的每一个元素定义为: (+1,支路k与回路j关联,且方向一致; - -1,支路k与回路j关联,且方向相反; 0,支路k不在回路j中(无关)。 bk:方向一致+1,方向相反-1,无关0。 21
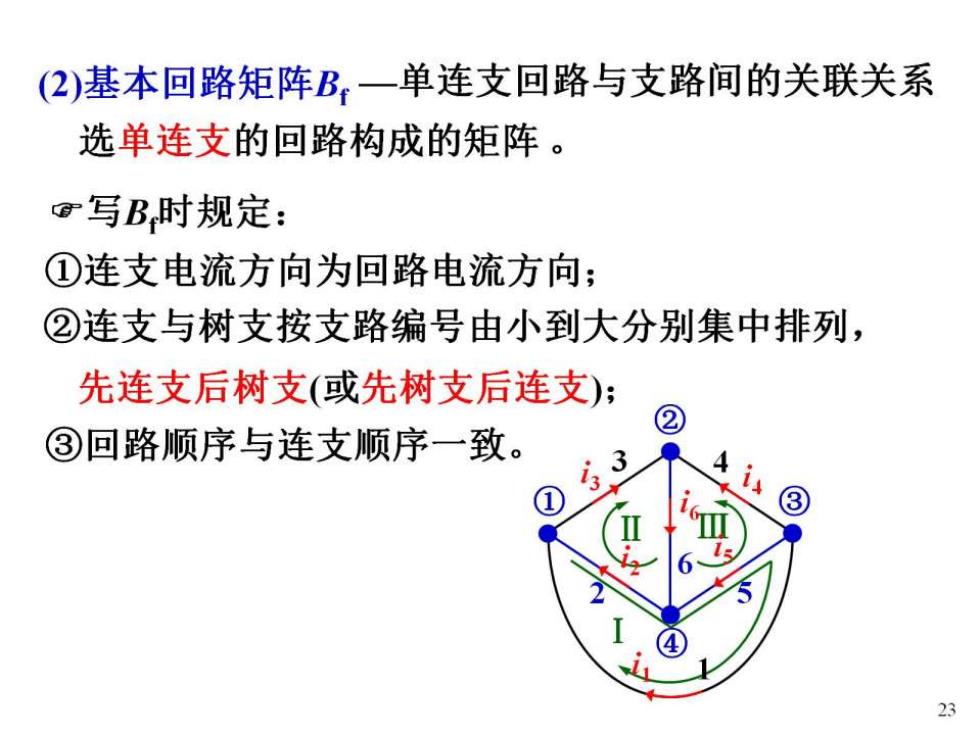
(2)基本回路矩阵B。一单连支回路与支路间的关联关系 选单连支的回路构成的矩阵。 写B时规定: ①连支电流方向为回路电流方向; ②连支与树支按支路编号由小到大分别集中排列, 先连支后树支(或先树支后连支); 2 ③回路顺序与连支顺序一致。 3 3 23
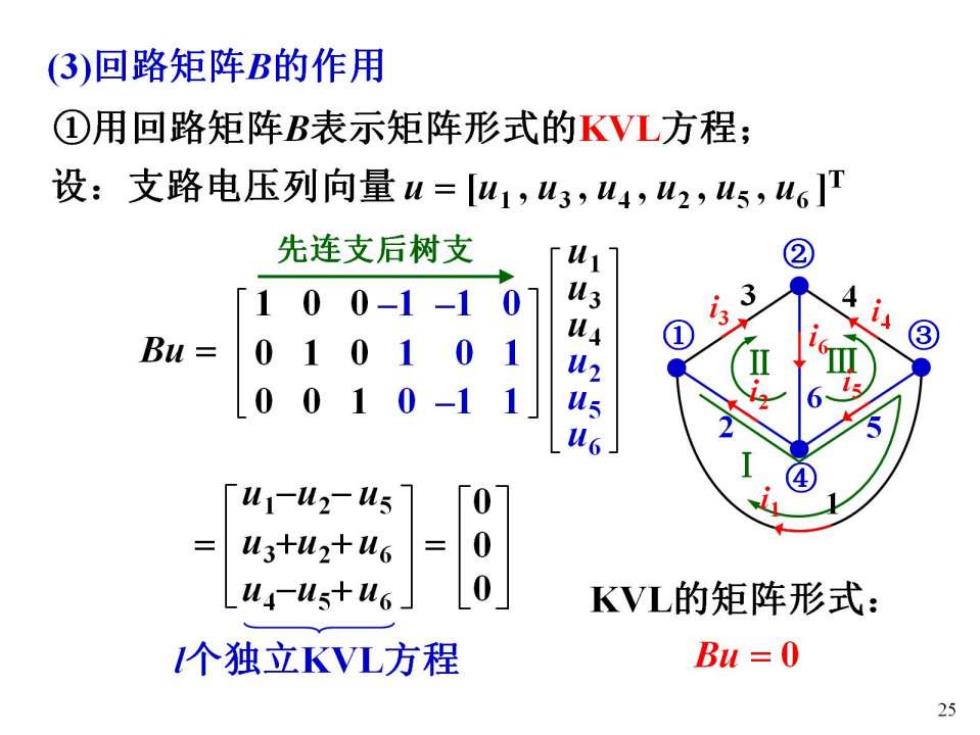
(3)回路矩阵B的作用 ①用回路矩阵B表示矩阵形式的KVL方程; 设:支路电压列向量u=u1,43,W4,u2,45,u6T 先连支后树支 [W1 ② Γ100-1 -10 u3 Bu= 01 ③ 00 -1 us us 「u1-u2-W5 0 u3+u2+u6 0 Lu4-us+u6」0 KVL的矩阵形式: 个独立KVL方程 Bu=0 25

②用回路矩阵BT表示矩阵形式的KCL方程 设:支路电流列向量i=[1,i3,4,2,5,6 回路电流列向量=,n,gT 10 0 in 0 1 0 in 0 BT i 01 _1 10 n g -1 0-1 .5 0 11 in+in KCL的矩阵形式:BTi=i 表明:各支路电路可以用与该支路关联的所有回路 中的回路电流表示。 26
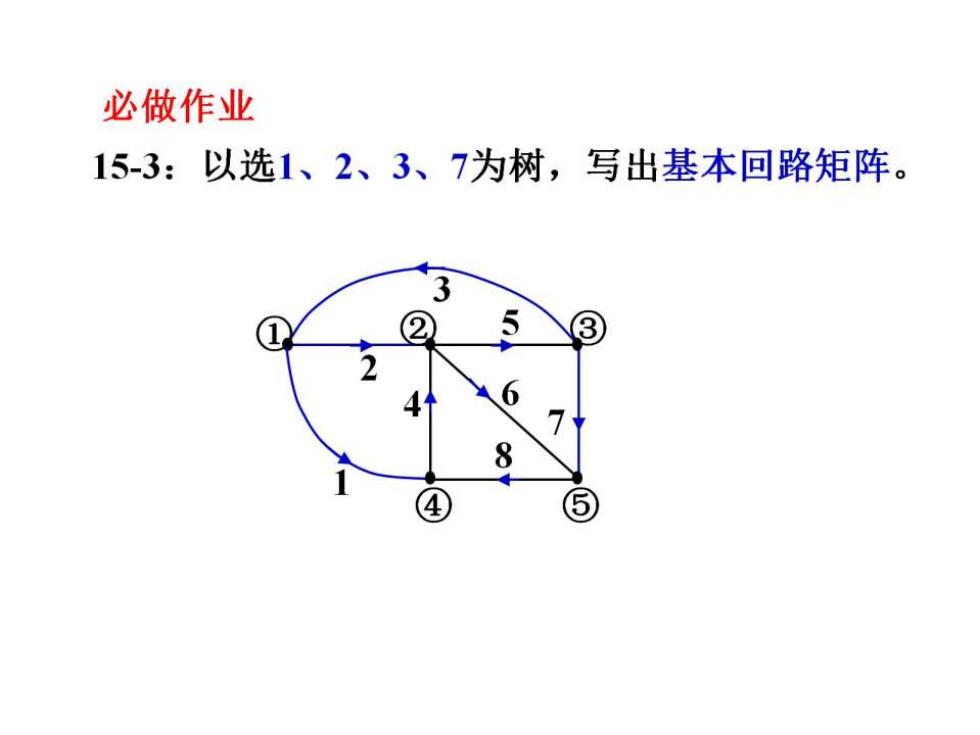
必做作业 15-3:以选1、2、3、7为树,写出基本回路矩阵