
15 .第1章无机材料的受力形变 能。如果在X平面上有n个位错,则在时间内总形变量△是n个位错滑移的累 积结果。也就是说,:时间内有n个位错将通过试样边界,而且还会引起位错增殖, 使通过边界的位错数增加到nc个,这里的系数c称为位错增殖系数。每个位错的运 动造成在运动方向上一个原子间距大小的滑移,即一个柏氏矢量的滑移,以b表示。 因此,在时间t内由于位错运动导致的滑移量为 nbc=△l (1.24) 于是试件的宏观应变速率可以写成 (1.25) 注意到参与形变的滑移平面上的位错密度为 D=是 (1.26) 位错运动的平均速度为 (1.27) 结合式(1.25)~式(1.27)可以得到 E=UDbc (1.28) 由式(1.28)可知,塑性形变速率取决于位错运动的速度元、位错密度D、柏氏矢 量b和位错增殖系数c。结构中具有足够的位错、位错在外力作用下能以足够高的速 度运动以及较大的柏氏矢量是一种材料发生显著的宏观塑性形变的三个基本前提。 关于柏氏矢量还需要作一些进一步的讨论。由于位错的形成需要能量,根据弹 性理论的计算,位错形成能为 E=aGb? (1.29) 式中,G为剪切模量;a为几何因子,其值为0.5~1.0;b为柏氏矢量。可见位错形 成能和成正比:b大形成位错所需的能量大,b小形成位错所需的能量小。b相当于 晶格的点阵常数。金属为一元结构,点阵常数较小(一般为3A左右,1A=100m), 因此金属材料的位错形成量小,容易形成位错。无机材料都是二元以上的多元化合 物,结构比较复杂,原子数较多(如MgAl2O4三元化合物,点阵常数约8A,A12O,的 点阵常数也在5A以上),位错形成能较大,因此无机材料中不易形成位错,加上位错 运动也很困难,因此难以产生塑性形变 最后指出一点,尽管理论分析表明,只要滑移面上的分剪应力足够高,任何一种 晶体材料内部的位错都可能以足够高的速度运动,从而使得品体表现出显著的塑性 形变,但是,对于大多数无机材料而言,当滑移面上的分剪应力尚未增大到能够使位 错以足够速度运动之前,此应力可能就已超过了微裂纹扩展所需的临界应力而导致 材料发生脆性断裂

16 无机材料物理性能 1.3.3塑性形变速率对屈服强度的影响 如上所述,在一定的剪应力x作用下,位错运动激活能H(x)减小。t愈大 H(x)愈小,从而位错运动速率元愈大,所以塑性形变速率E与所受剪应力:的大小 有关。 在900℃下采用不同形变速率对Al2O,单晶试样进行拉伸试验,结果示于 图1.12(b)。可以看出,随着形变速率的增大,氧化铝单晶的屈服强度也相应增大 从微观上看,这相当于滑移系统的临界剪应力随宏观形变速率的增大而增大。对其 他一些材料的研究也得到了类似的结果。 分析表明,无机材料的塑性形变速率E与屈服强度,之间存在如下的经验 关系: =()M (1.30) 式中,m为位错运动速率的应力敏感性指数。室温下一些材料的m值列于表1.3。 表1.3室温下不同材料的应力敏感性指数 材料 结 构 LiF 岩盐型 13.521 岩盐型 7.829.5 MgO 岩盐型 2.5≈6 CaF, 董石型 7 Si 金刚石型 1.4~1.5 1.4高温下玻璃相的黏性流动 在高温下,玻璃或无机材料中的晶界玻璃相在剪应力作用下会发生不同程度的 黏性流动。黏性流动的特点是剪应力与速度梯度成正比,即: t-1 dx d (1.31) 式中的比例常数7称为黏性系数或黏度,是材料的性能参数。其单位为Pa·5。 式(1.31)称为牛顿定律。符合牛顿定律的流体叫做牛顿液体,其特点为应力与 应变率之间呈直线比例关系。大多数情况下,氧化物流体可看成是牛顿液体。 1.4.1流动模型 为了揭示黏性流动的本质,曾经提出过多种流动模型。下面简单介绍其中的 种 一绝对速率理论模型。 绝对速率模型的出发点是认为液体的流动是一个速率过程,任一液体层相对于 邻层液体流动时,液体分子从开始的平衡状态过渡到另一平衡状态。其间,液体分子
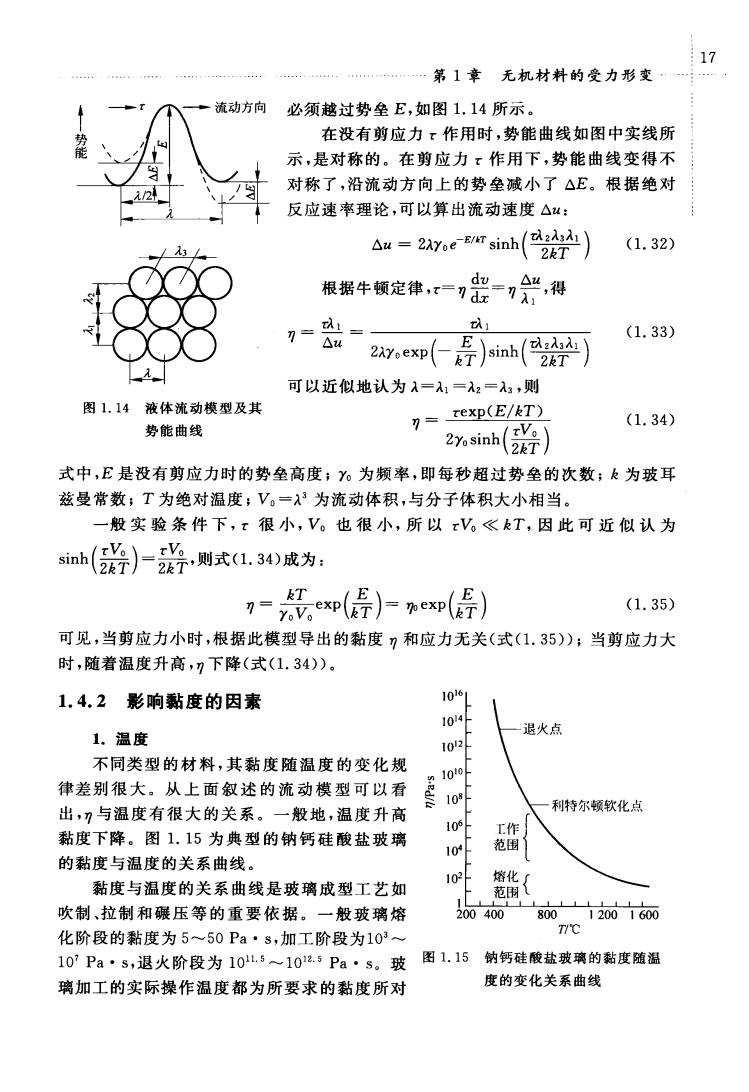
17 .第1章无机材料的受力形变 流动方向 必须越过势垒E,如图1.14所示。 在没有剪应力?作用时,势能曲线如图中实线所 示,是对称的。在剪应力x作用下,势能曲线变得不 对称了,沿流动方向上的势垒减小了△E。根据绝对 反应速率理论,可以算出流动速度△u: aw=2 sinh(222) (1.32) 根据牛顿定律,=品尝,得 = (1.33) △4 2ep(←导)sinh(2¥】 可以近似地认为入=1=入2=,则 图1.14液体流动模型及其 习=rXp(E/T) 2%sinh(器】 (1.34) 势能曲线 式中,E是没有剪应力时的势垒高度;。为频率,即每秒超过势垒的次数;k为玻耳 兹曼常数;T为绝对温度,V。=为流动体积,与分子体积大小相当。 一般实验条件下,x很小,V。也很小,所以xV。《kT,因此可近似认为 snh(必)-若则式1.30成为: 7=0得)-ep(导) (1.35) 可见,当剪应力小时,根据此模型导出的黏度?和应力无关(式(1.35));当剪应力大 时,随着温度升高,?下降(式(1.34))。 1.4.2影响黏度的因素 1061 1.温度 一退火点 10 不同类型的材料,其黏度随温度的变化规 律差别很大。从上面叙述的流动模型可以看 出,刀与温度有很大的关系。一般地,温度升高 利特尔顿软化点 106 黏度下降。图1.15为典型的钠钙硅酸盐玻璃 的黏度与温度的关系曲线。 10 甜 黏度与温度的关系曲线是玻璃成型工艺如 102 吹制、拉制和碾压等的重要依据。一般玻璃熔 20040080012001600 化阶段的黏度为5~50Pa·s,加工阶段为103~ 102Pa·s,退火阶段为10l.5~10.5Pa·s。玻 图1.15钠钙硅酸盐玻璃的黏度随涅 璃加工的实际操作温度都为所要求的黏度所对 度的变化关系曲线
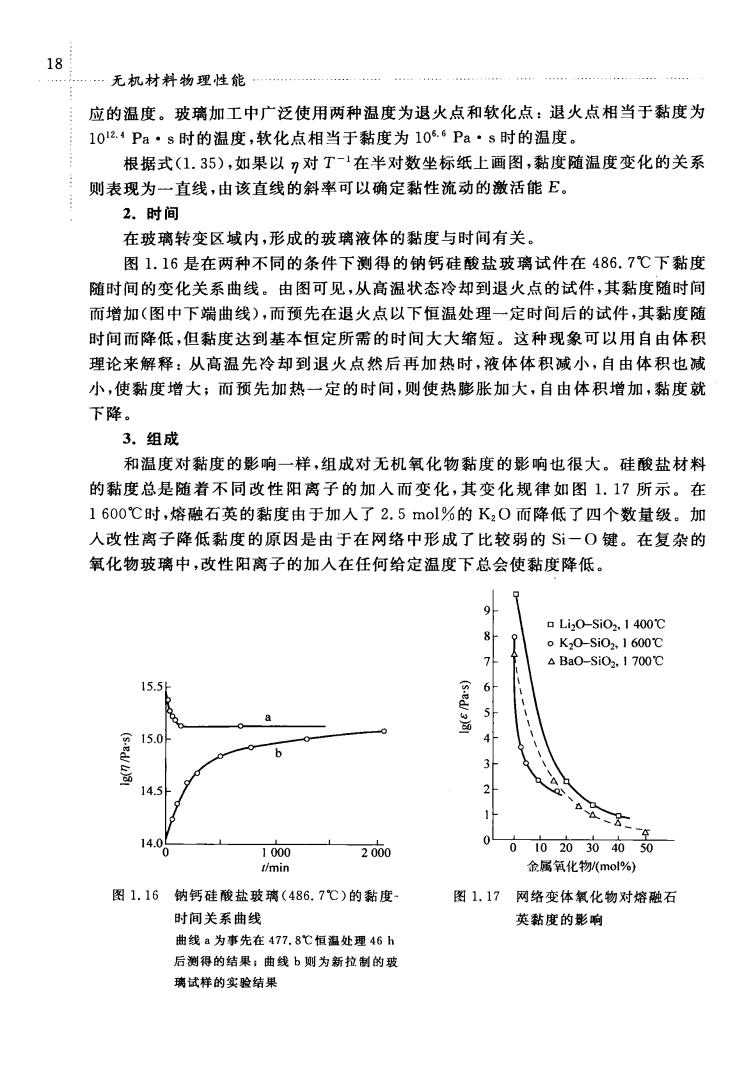
.无机材料物理性能. 应的温度。玻璃加工中广泛使用两种温度为退火点和软化点:退火点相当于黏度为 1024Pa·s时的温度,软化点相当于黏度为10s.‘Pa·s时的温度。 根据式(1.35),如果以?对T-1在半对数坐标纸上画图,黏度随温度变化的关系 则表现为一直线,由该直线的斜率可以确定黏性流动的澈活能E。 2.时间 在玻璃转变区域内,形成的玻璃液体的黏度与时间有关」 图1.16是在两种不同的条件下测得的钠钙硅酸盐玻璃试件在486.7℃下黏度 随时间的变化关系曲线。由图可见,从高温状态冷却到退火点的试件,其黏度随时间 面增加(图中下端曲线),而预先在退火点以下恒温处理一定时间后的试件,其黏度随 时间而降低,但黏度达到基本恒定所需的时间大大缩短。这种现象可以用自由体积 理论来解释:从高温先冷却到退火点然后再加热时,液体体积减小,自由体积也减 小,使黏度增大;而预先加热一定的时间,则使热膨张加大,自由体积增加,黏度就 下降。 3.组成 和温度对黏度的影响一样,组成对无机氧化物黏度的影响也很大。硅酸盐材料 的黏度总是随着不同改性阳离子的加入而变化,其变化规律如图1.17所示。在 1600℃时,熔融石英的黏度由于加人了2.5mol%的K20而降低了四个数量级。加 人改性离子降低黏度的原因是由于在网络中形成了比较弱的S一O键。在复杂的 氧化物玻璃中,改性阳离子的加入在任何给定温度下总会使黏度降低。 aLi,0-si02.14000 6 4 14 1000 2000 03040 20 t/min 金属氧化物mol% 图1.16钠钙硅酸盐玻璃(486.7℃)的黏度 图1.17网络变体氧化物对熔融石 时间关系曲线 英黏度的影响 曲线a为事先在477,8℃恒温处理46 后测得的结果;曲线b则为新拉制的玻 璃试样的实验结果

19 .第1章无机材料的受力形变 1.5无机材料的高温蠕变 1,5.1黏弹性与滞弹性 在一些特定的情况下,一些非晶体和多晶体在受到比较小的应力作用时可以同 时表现出弹性和黏性,这种现象称为黏弹性。所有聚合物差不多都表现出这种黏 弹性。 理想的弹性体在受到应力作用时会立即引起弹性应变,而一旦应力消除,弹性应 变也随之立刻消除。对于实际固体,弹性应变的产生与消除都需要有限的时间。无 机固体和金属表现出的这种与时间有关的弹性称为滞弹性。聚合物的黏弹性可以认 为仅仅是严重发展的滞弹性。此外,金属材料在高温受力时发生的塑性变形也具有 一些滞弹性的成分 在转变温度附近的玻璃以及高温下许多含有玻璃相的材料,弹性模量不再是和 时间无关的参数,而是随时间的增加而降低。这是由于高温下,应力的持续作用将使 一些原子从一个位置移动到另一位置。在这种情况下,形变是滞弹性或黏弹性的。 这种形变绝大部分在应力除去后或施加相反方向的应力时可以恢复,但不是瞬时恢 复,而是逐渐恢复。 当对黏弹性体施加恒定应力时,其应变随时间而增加。这种现象叫做蠕变, 此时弹性模量E。也将随时间而减小: E.)=E& (1.36) 如果施加恒定应变©,则应力将随时间而减小,这种现象叫做弛豫。此时弹性模 量E,也随时间而降低: E,()=() (1.37) 通常采用弹簧表示满足胡克定律的弹性元件,用 其中有一活塞并充满黏性液体的圆简来表示符合牛 顿定律的黏性元件,见图1.18。用这两种元件进行 (a) (b) 各种组合便可以得到各种不同的模型,以分析材料在 图1.18弹性及黏性元件模型 不同条件下表现出的不同的变形行为。 图1.19(a)就是通常用来分析滞弹性行为的力学 (a)弹性元件:6-是及y=言, 模型。这一力学模型所表示的物体通常称为标准线 (b)黏性元件:=马及 性固体。根据这一模型,具有弛豫性状的固体材料的 总应变为 -7(-密-盘) E=E1十e=弹2 (1.38a) 总应力则为