
20 .无机材料物理性能 时间 (a) (b) 图1.19具有弛豫性能的标准线性固体 (a)模型:(b)力学性能 g=0爆1十w2=E装十E2e绿2 (1.38b) 由式(1.38a), ==-:=-(官-受) -()-B吉B)-是 代入式(1.38b)得到 +毫-(吉)+ (1.39) 或 E2(xE十e=xd+a (1.40) 式中,/E,为恒定应变下的应力弛豫时间:6,=(十B)×x,为恒定应力下应 E2 变蠕变时间。它们都表示材料在外力作用下从不平衡状态通过内部结构重新组合而 达到平衡状态所需的时间。如果材料的?大,E小,则x和。都大,说明滞弹性也 大。如果刀=0,则x,=0,=0,弹性模量为常数,不随时间变化,表现出真正的弹性。 在测定滞弹性材料的形变时,如果测量时间小于,和x。,则由于随时间的形变 还没有机会发生,测得的是应力和初始应变的关系,这时的弹性模量叫未弛像模量: 如果测量的时间大于x,和x。,测得的则是弛豫模量。显然,弛豫模量总小于未弛豫 模量。 材料在外力作用下从不平衡状态通过内部结构重新组合而达到平衡状态,其间 将可能发生很多个不同的组合过程,因此仅仅用标准线性固体模型还不能很好地描 述材料的滞弹性,对滞弹性行为的完整描述需要用很多个蠕变或弛豫模型的组合来 表示。这样,蠕变时间或弛豫时间就不再是一个常数,而是有一个分布,这个分布 般是0~∞这一区间的连续的时间谱。 在多晶陶瓷中,滞弹性弛豫最主要的根源是材料内部残余的玻璃相。这种残余
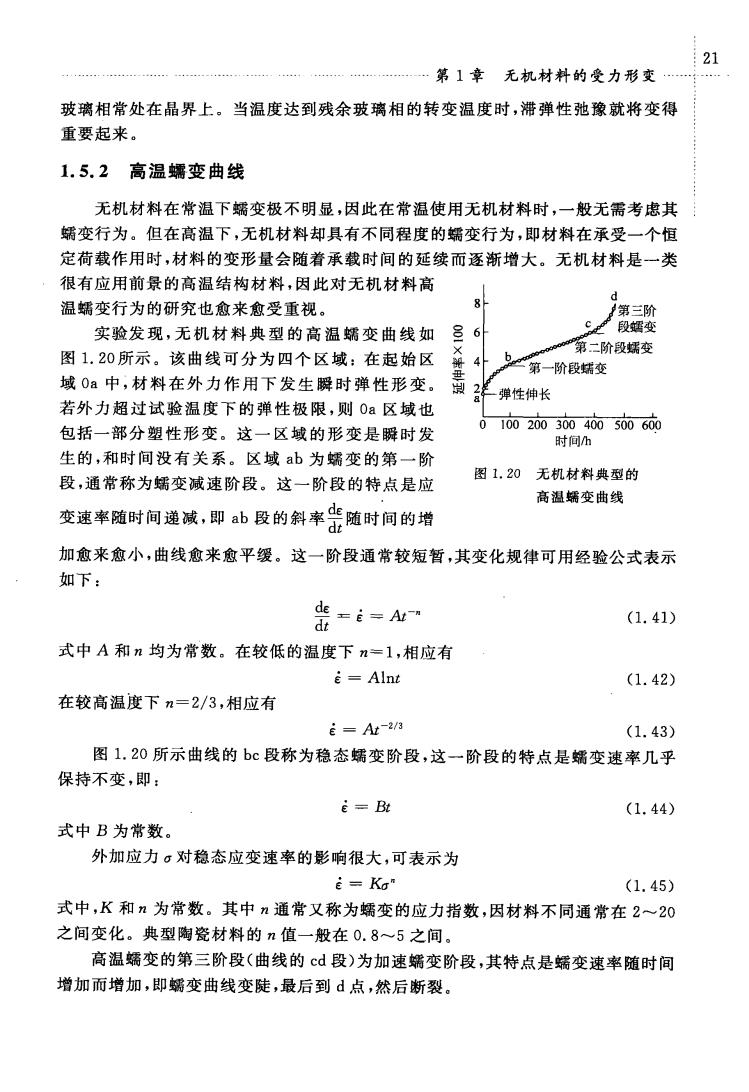
21 .第】章无机材料的受力形变. 玻璃相常处在晶界上。当温度达到残余玻璃相的转变温度时,滞弹性弛豫就将变得 重要起来。 1.5.2高温蠕变曲线 无机材料在常温下蠕变极不明显,因此在常温使用无机材料时,一般无需考虑其 蠕变行为。但在高温下,无机材料却具有不同程度的蠕变行为,即材料在承受一个恒 定荷载作用时,材料的变形量会随着承载时间的延续而逐渐增大。无机材料是一类 很有应用前景的高温结构材料,因此对无机材料高 温蠕变行为的研究也愈来愈受重视。 第三阶 实验发现,无机材料典型的高温蠕变曲线如三6 C段里变 图1.20所示。该曲线可分为四个区域:在起始区 h 第二阶段蠕变 二第一阶段蠕交 域0a中,材料在外力作用下发生瞬时弹性形变。 弹性伸长 若外力超过试验温度下的弹性极限,则Oa区域也 包括一部分塑性形变。这一区域的形变是瓣时发 01002003004005006 时间公 生的,和时间没有关系。区域ab为蠕变的第一阶 段,通常称为蠕变减速阶段。这一阶段的特点是应 图1.20无机材料典型的 高温蠕变曲线 变速率随时间递减,即b段的斜率随时间的增 加愈来愈小,曲线愈来愈平缓。这一阶段通常较短暂,其变化规律可用经验公式表示 如下, 盖=i= (1.41) 式中A和n均为常数。在较低的温度下n=1,相应有 =Alnt (1.42) 在较高温度下n=2/3,相应有 E=A-23 (1.43) 图1.20所示曲线的bc段称为稳态蠕变阶段,这一阶段的特点是蠕变速率几乎 保持不变,即: i=Bt (1.44) 式中B为常数 外加应力。对稳态应变速率的影响很大,可表示为 E=Ka" (1.45) 式中,K和n为常数。其中n通常又称为蠕变的应力指数,因材料不同通常在2~20 之间变化。典型陶瓷材料的n值一般在0.8~5之间。 高温蠕变的第三阶段(曲线的©d段)为加速蠕变阶段,其特点是蠕变速率随时间 增加而增加,即蠕变曲线变陡,最后到点,然后断裂

22 无机材料物理性能 当外力和温度不同时,虽然蠕变曲线仍保持上 述几个阶段的特点,但各段所延续的时间及曲线的 倾斜程度将有所不同。图1.21示出了蠕变曲线随 温度和应力的变化而变化的一些基本规律。由图中 可以看出,当温度或应力较低时,稳态孀变阶段延 长,当应力或温度增加时,稳定态蠕变阶段缩短,甚 至不出现。 蠕变曲线的实验测定是研究无机材料高温蠕变 行为的基础。蠕变曲线的测定涉及许多参数,包括 测试的环境、温度、湿度以及材料的受力方式、受力 时间 大小、材料变形量随承载时间的变化等。蠕变曲线 图1.21温度和应力对蠕变 测定的主要内容是应变随时间的变化关系曲线,并 曲线的影响 由之确定材料蠕变的极限变形值。、稳态蠕变阶段 的蠕变应力指数”、稳态蠕变速率:以及在给定应力水平作用一定时间后的蠕变应 变量等。 1.5.3高温蠕变理论 无机材料多为多品多相材料,各相之间的耐火度差别较大,因此无机材料的蠕变 行为受环境温度的影响很大,同时也强烈地依赖于材料的显微结构。蠕变本身是 种属于宏观尺度的整体性能指标。研究表明,评价材料蠕变性能的主要参数之 一在指定温度下的稳态蠕变速率与材料的结构、性能以及环境因素等之间存 在如下关系: =A(倍)广()广密 (1.46) 式中,G为材料的剪切模量;b为柏氏矢量;d为品粒尺寸;▣为外加应力;T为绝对 温度:R为气体常数:D-Dex即(仁是导)为扩散系数:Q为扩散激活能:A,m和n 均为常数。其中n即为式(1.45)中的蠕变应力指数。 不同材料在不同环境温度下高温蠕变的机理不同,主要受材料在显微结构尺度 上的各种变形机制所制约。在过去儿十年中,学者们为解释无机材料的高温蠕变机 理已经提出了一些相应的理论,大致可以分为晶格蠕变和品界蠕变这两大类。 1.晶格蠕变 晶格蠕变一般发生在晶体内部,其微观机理主要有两种:一种是以位错的运动 为主,是一类在长程应力场作用下所形成的位错滑移蠕变;另一种则是由晶格中的 点缺陷(如空穴、填隙原子等)的扩散导致的,属于短程应力场中的扩散蠕变。位错滑 移蠕变多发生在中、高温下承受10~1000MPa拉应力作用的情况下,而扩散蠕变则

23 .第1章无机材料的受力形变·. 多发生在高温下承受低于10MPa的低压力情况下(晶粒扩散)或者在中低温度下受 低应力作用的情况下(品界扩散)。 由于晶格蠕变发生在晶体内部,因此其稳态蠕变速率与晶粒尺寸无关,即 式(1.46)中的m=0,相应地,稳态蠕变速率的表达式为 i=Aep(-号)片 (1.47) 与式(1.46)相比较,式(1.47)中的常数A.包括了材料的剪切模量、柏氏矢量以及 其他一些基本常数,而参数Q则为克服长程位错滑移或晶格点缺陷扩散的激活能。 金属材料晶格蠕变的应力指数为5,合金品格蠕变的应力指数为3,而大多数无 机材料的晶格蠕变应力指数则处于3一4.5之间。 2.晶界蠕变 多晶多相材料中存在着大量的非晶态晶界相。在高温下,晶界相黏度迅速下降 外力的作用会导致晶界发生黏滞流动,从而引起材料的蠕变。一般说来,无机材料的 蠕变在很大程度上取决于其晶界相的状态及其含量。 无机材料的晶界蠕变大致分为三种情况。 (1)对于低熔点的工业陶瓷,晶界相所占的比例相对较大,晶界相尺度也相对较 厚,在高温下易于发生品界相的黏滞流动。如果将高温下发生黏滞流动的晶界相近 似处理为牛顿流体,则这类材料的稳态蠕变速率可以表述为 =Ar (1.48) 式中,x为晶界所受到的剪切应力;D为晶界相的扩散系数;A为常数。 与式(1.46)相比较不难看出,对于由式(1.48)所描述的这类蠕变有:m=1,n 1。但是必须指出的是,如果上面所讨论的晶界相不是玻璃态,而是微晶态,则n≠1。 (2)如果晶界相含量较少,相应的晶界相厚度较小,蠕变则主要表现为晶界的滑 移,同时伴随有晶粒本身的变形。大多数高性能陶瓷和新型耐火材料在高温受力时 基本上都将发生这一类蠕变。 晶界滑移导致的蠕变多由扩散过程控制。如果扩散过程主要发生在晶粒内部, 则称为Nabarro-Herring蠕变。Nabarro-Herring蠕变的机理大致为:晶格点缺陷 的扩散使晶粒沿主拉应力方向伸长、变细,致使各晶粒之间的形变发生失配,从而引 起晶界的滑移。在这种情况下,晶界的滑移导致的形变占据了材料总蠕变形变量的 主要部分。Nabarro和Herring将晶界处理为理想的牛顿流体,导出了这类蠕变的 稳态蠕变速率表达式如下: (1.49) 与式(1.47)相比较,这类蠕变的m值为2,即稳态蠕变速率与晶粒表面积(cd产) 成反比,说明这一类晶界滑移主要受晶粒表面积所制约。 如果扩散过程主要发生在晶界相,则称为Coble蠕变。Coble蠕变主要是由于

.无机材料物理性能 受拉晶界和受压晶界之间产生的空位浓度差导致的受拉晶界处空位向受压晶界处迁 移的结果。此时虽然也会发生晶粒内部点缺陷的扩散,但点缺陷的扩散对晶界迁移 的作用一般可以忽略不计。根据Coble的推导,在晶界相可以近似处理为牛顿流体 的前提下,这类蠕变的稳态蠕变速率表达式为 =B兽(传层2) (1.50) 式中,db为晶界相的平均厚度。注意到式中(b/d)项的指数为3,说明Coble蠕变主 要受晶粒所占的体积大小所制约。 (3)对于一些晶界相含量较少,晶界相厚度相应较小的无机材料,蠕变有时也可 能完全(或近乎完全)由晶界的滑移控制。在这类蠕变过程中,晶粒几乎不会发生任 向程度的形变。根据晶果相状态的不同,这类绣变也有两种不同的情祝。如果品界 相是非晶态并且可以近似处理为牛顿流体,则晶界相的流动与晶粒尺寸成反比,即 m=1,此时,稳态蠕变速率为 =16P0(怡)() (1.51) 而如果晶界相是非晶态但不能视为牛顿流体,此时晶界的滑移将由另外的机制 主导。由于外加应力的作用,晶界的一些薄弱点尤其是三交晶界处可能会形成孔洞; 这些孔洞的长大、伸长、连通在宏观就会表现为材料变形量的增大(即蠕变)。这种变 形属于弹黏体的变形,其蠕变应力指数大致在2左右,其稳态蠕变速率则为 E=B(台)() (1.52》 1.5.4蠕变断裂 无论是晶格蠕变,还是晶界蠕变,蠕变的最终结果大多都将是断裂。也就是说, 当蠕变变形量达到一定程度之后,材料就会发生蠕变断裂。 对于晶格蠕变,位错的运动在晶粒表面附近受阻,或者点缺陷的扩散使得点缺陷 在晶粒表面附近富集,其结果就是在晶粒表面附近形成一个较大的缺陷,随着承载 时间的延续,蠕变变形量的增大,晶粒表面处聚集的缺陷逐渐发育,当缺陷尺寸达到 某一临界值时,在外力作用下就将发生灾难性扩展导致材料的断裂。晶格蠕变引发 的断裂主要表现为穿晶断裂。 对于晶界蠕变,情况基本类似。晶界的滑移将使得类裂纹在晶界的一些薄弱点 尤其是在三交晶界处形成,这些类裂纹在蠕变过程逐渐发育长大到临界尺寸后发生 失稳扩展导致材料断裂。晶界蠕变引发的断裂主要表现为沿晶断裂。 我们在第3章中还将就蠕变断裂问题展开更进一步的讨论。 1.5.5影响蠕变的因素 从上面的讨论可知,影响蠕变的因素很多。这里我们主要从以下几个方面展开 讨论