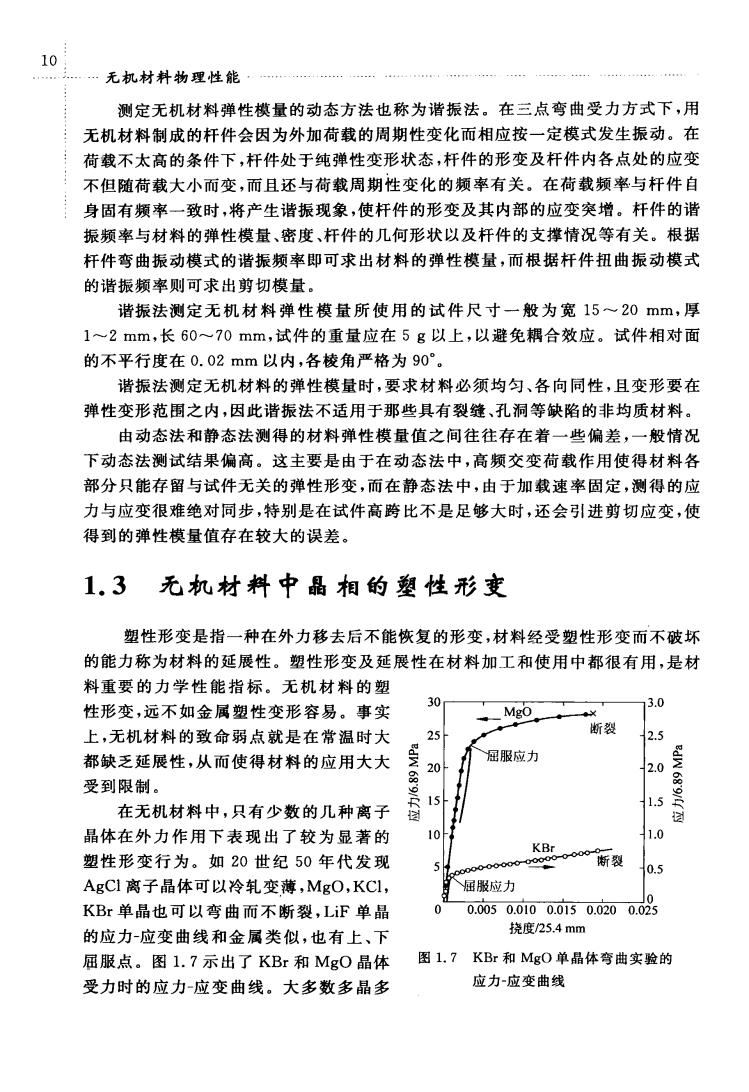
o 无机材料物理性能 测定无机材料弹性模量的动态方法也称为谐振法。在三点弯曲受力方式下,用 无机材料制成的杆件会因为外加荷载的周期性变化而相应按一定模式发生振动。在 荷载不太高的条件下,杆件处于纯弹性变形状态,杆件的形变及杆件内各点处的应变 不但随荷载大小而变,而且还与荷载周期性变化的频率有关。在荷载频率与杆件自 身固有频率一致时,将产生谐振现象,使杆件的形变及其内部的应变突增。杆件的谐 振频率与材料的弹性模量、密度、杆件的几何形状以及杆件的支撑情况等有关。根据 杆件弯曲振动模式的谐振频率即可求出材料的弹性模量,而根据杆件扭曲振动模式 的谐振频率则可求出剪切模量。 谐振法测定无机材料弹性模量所使用的试件尺寸一般为宽15~20mm,厚 1~2mm,长60~70mm,试件的重量应在5g以上,以避免耦合效应。试件相对面 的不平行度在0.02mm以内,各棱角严格为90°。 谐振法测定无机材料的弹性模量时,要求材料必须均匀、各向同性,且变形要在 弹性变形范围之内,因此谐振法不适用于那些具有裂缝、孔洞等缺陷的非均质材料。 由动态法和静态法测得的材料弹性模量值之间往往存在着一些偏差,一般情况 下动态法测试结果偏高。这主要是由于在动态法中,高频交变荷载作用使得材料各 部分只能存留与试件无关的弹性形变,而在静态法中,由于加载速率固定,测得的应 力与应变很难绝对同步,特别是在试件高跨比不是足够大时,还会引进剪切应变,使 得到的弹性模量值存在较大的误差。 1.3 无机材料中晶相的塑性形变 塑性形变是指一种在外力移去后不能恢复的形变,材料经受塑性形变而不破坏 的能力称为材料的延展性。塑性形变及延展性在材料加工和使用中都很有用,是材 料重要的力学性能指标。无机材料的塑 性形变,远不如金属塑性变形容易。事实 30 3.0 上,无机材料的致命弱点就是在常温时大 2. 都缺乏延展性,从而使得材料的应用大大 20 屈服应力 受到限制。 在无机材料中,只有少数的几种离子 晶体在外力作用下表现出了较为显著的 1.0 塑性形变行为。如20世纪50年代发现 KBr 新裂 0.5 AgC1离子品体可以冷轧变薄,MgO,KCl, 屈散应力 KBr单晶也可以弯曲而不断裂,LiF单晶 0.0050.0100.0150.0200.03品3 的应力应变曲线和金属类似,也有上、下 挠度25.4mm 屈服点。图1.7示出了KBr和MgO晶体 图L.7KBr和MgO单品体弯曲实验的 受力时的应力应变曲线。大多数多晶多 应力应变曲线

11 一第一章无机材料的受力形变 相无机材料在常温下都不具延展性,也就是说没有或只有很小的塑性形变。最近发 现,含CeO2的四方ZO2多晶瓷在应力超过一定值后,表现出很大的塑性变形,因为 这种变形是由四方ZO,相变为单斜ZO2引起的,所以称为相变塑性或超塑性。 为什么常温下大多数无机材料不能产生塑性形变?回答这个问题首先要研究塑 性形变的机理。我们先从单晶入手,这样可以不考虑晶界的影响。 1.3.1晶格滑移 晶体中的塑性形变有两种基本方式:滑移和孪晶。由于滑移现象在晶体中最为 常见,所以这里我们主要讨论晶体的滑移。 在受力作用时,晶体的一部分相对于另一部分发生的平移滑动叫做滑移。晶体 发生滑移后,表面会出现一些条纹,在显微镜下可以看到由这些条纹组成的一些滑移 带,如图1.8(a)所示。图1.8(b)为滑移现象的微观示意图。 。 李品 (b) 图1.8品体的滑移示意图 晶体中的滑移总是发生在一些特定的晶面和晶向上,这些晶面和晶向指数较小, 原子密度大,也就是柏氏矢量6较小,只要滑动较小的距离就能使晶体结构复原,所 以比较容易滑动。滑动面和滑动方向组成品体的滑移系统,而滑移则是在剪应力作 用下在一定滑移系统上进行的。 例如NaC1型结构的离子晶体,其滑移系统通常是(110}面族和<110>晶向。 图1.9所示为NaC型结构离子晶体沿(110>方向发生滑移的示意图。可以看出: ①从几何因素考虑,在(110)面,沿〈110》方向滑移,同号离子间柏氏矢量较小 ②从静电作用因素考虑,在滑移过程中不会遇到同号离子的巨大斥力,因此,在(110) 面上,沿110>方向滑移比较容易进行。 拉伸或压缩都会在滑动面上产生剪应力。由于滑移面的取向不同,其上的剪应 力也不同。现在我们以单品受拉为例,看看滑移面上的剪应力要多大才能引起滑移。 截面积为A的圆柱形单晶体,在受拉力F作用时在滑移面上沿滑移方向发生的 滑移如图1,10所示。不难看出,滑移面上F方向的应力为

无机材料物理性能. 移 (a) (b) 图1.9NaC1型结构离子晶体沿<110>方向的平移滑动 图1.10圆柱形单晶特定滑移面 (a)在110)面族上,(b)在100面族上 ·上剪应力的确定 F a-Alcosep 此应力在滑移方向上的剪应力分量为 (1.22) A 式(1.22)表明,不同滑移面及滑移方向上的剪应力不一样;同一滑移面上不同滑移 方向,剪应力也不一样。由于滑移面的法线N总是和滑移方向垂直。当P角与入角 处于同一平面时,1角最小,即1+p=90°,所以cos1·cosp的最大值为0.5。可见, 在外力F作用下,在与N,F处于同一平面内的滑移方向上,剪应力达最大值,其他 方向剪应力均较小。 使晶体在一个特定的滑移系统中发生滑移所需要的最低剪应力称为该滑移 系统的临界剪应力,也就是说只有当x≥时晶体才会发生滑移。不同滑移系统的 临界剪应力之间有很大的差别。 显然,如果一种晶体的滑移系统数目较少,则产生滑移的机会就很小。滑移系 统多的话,对其中一个滑移系统来说,可能c0s以·cosp较小,但对另一个系统来说, cos以·cOsp可能就会比较大,因此某一滑移系统满足滑移条件(即滑移系统受到的剪 应力达到或超过临界剪应力)的机会就较多。金属易于滑移而产生塑性形变,就是因 为金属滑移系统很多,如体心立方金属(铁、铜等)滑移系统有48个之多,而无机材料 的滑移系统却非常少。此外,金属材料中的金属键是没有方向性的,而大多数无机材 料的原子结构是共价健、离子键或者二者的混合型,破坏这些具有极强方向性的键远 比破坏金属键困难得多,因此只有为数不多的无机材料晶体在室温下具有延展性, 这些晶体都是具有NaC1型结构的最简单的离子晶体,如AgCl、KCl、MgO、KBr、Li
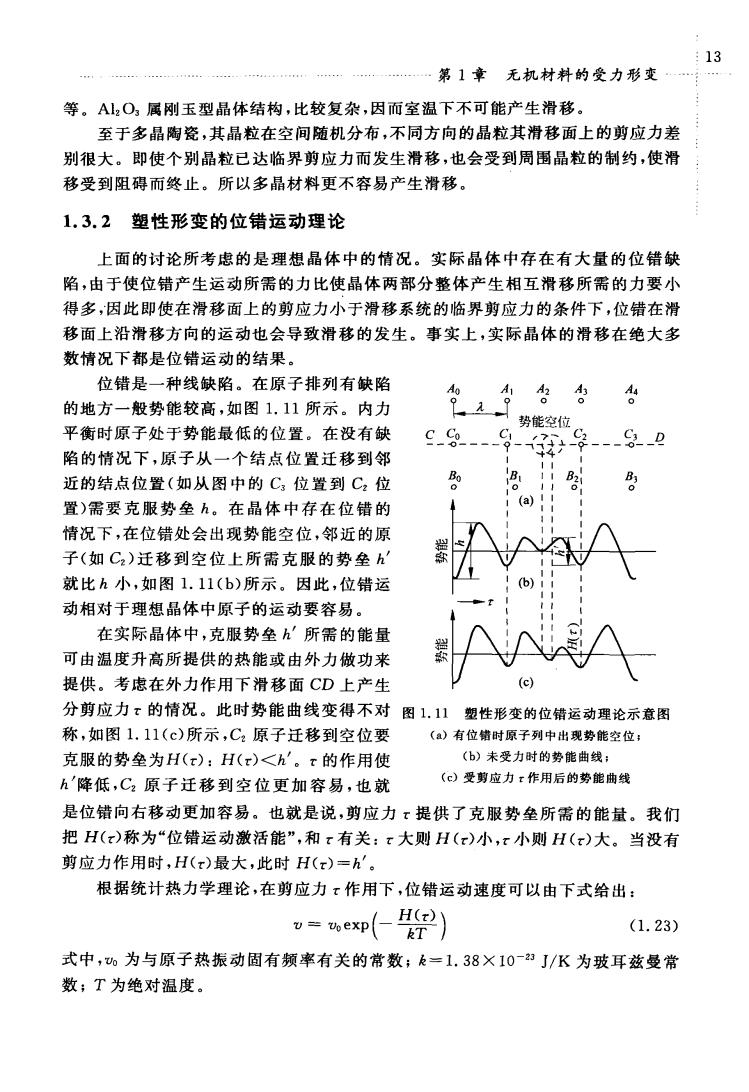
13 .第1章无机材料的受力形变 等。AlzO,属刚玉型晶体结构,比较复杂,因而室温下不可能产生滑移 至于多晶陶瓷,其晶粒在空间随机分布,不同方向的品粒其滑移面上的剪应力差 别很大。即使个别晶粒已达临界剪应力而发生滑移,也会受到周围晶粒的制约,使滑 移受到阻得而终止。所以多晶材料更不容易产生滑移 1.3.2塑性形变的位错运动理论 上面的讨论所考虑的是理想晶体中的情况。实际晶体中存在有大量的位错缺 陷,由于使位错产生运动所需的力比使晶体两部分整体产生相互滑移所需的力要小 得多,因此即使在滑移面上的剪应力小于滑移系统的临界剪应力的条件下,位错在滑 移面上沿滑移方向的运动也会导致滑移的发生。事实上,实际晶体的滑移在绝大多 数情况下都是位错运动的结果 位错是一种线缺路。在原子排列有缺路 的地方一般势能较高,如图1,11所示。内力 势能空位 平衡时原子处于势能最低的位置。在没有缺 陷的情况下,原子从一个结点位置迁移到邻 近的结点位置(如从图中的C位置到C,位 置)需要克服势垒h。在晶体中存在位错的 (a) 情况下,在位错处会出现势能空位,邻近的原 子(如C:)迁移到空位上所需克服的势垒h' 就比h小,如图1.11(b)所示。因此,位错运 动相对于理想晶体中原子的运动要容易。 在实际晶体中,克服势垒h'所需的能量 可由温度升高所提供的热能或由外力做功来 提供。考虑在外力作用下滑移面CD上产生 (c) 分剪应力x的情况。此时势能曲线变得不对 图1.11塑性形变的位错运动理论示意图 称,如图1.11(c)所示,C:原子迁移到空位要 ()有位结时原子列中出现势能空位: 克服的势垒为H(x):H(x)<h'。x的作用使 (b)未受力时的势能曲线: h'降低,C2原子迁移到空位更加容易,也就 (⊙受剪应力:作用后的势能 是位错向右移动更加容易。也就是说,剪应力x提供了克服势垒所需的能量。我们 把H(x)称为“位错运动激活能”,和x有关:x大则H(r)小,x小则H(x)大。当没有 剪应力作用时,H(x)最大,此时H(x)=h'。 根据统计热力学理论,在剪应力x作用下,位错运动速度可以由下式给出: (1.23) 式中,功为与原子热振动固有频率有关的常数;k=1.38×10”J/K为玻耳兹曼常 数;T为绝对温度
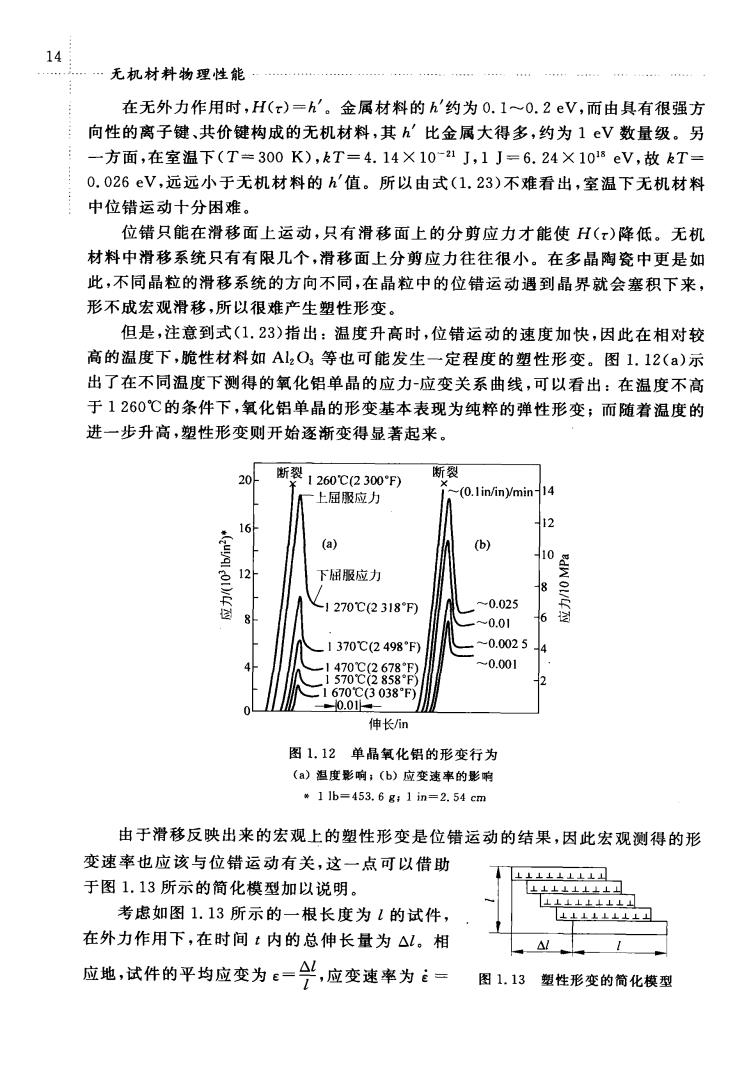
14 无机材料物理性能 在无外力作用时,H(x)=h'。金属材料的h'约为0.1~0.2eV,而由具有很强方 向性的离子键、共价键构成的无机材料,其h'比金属大得多,约为1eV数量级。另 一方面,在室温下(T=300K),kT=4.14×10-1J,1J=6.24×108eV,故kT= 0.026eV,远远小于无机材料的h'值。所以由式(1.23)不难看出,室温下无机材料 中位错运动十分困难。 位错只能在滑移面上运动,只有滑移面上的分剪应力才能使H(x)降低。无机 材料中滑移系统只有有限几个,滑移面上分剪应力往往很小。在多晶陶瓷中更是如 此,不同晶粒的滑移系统的方向不同,在晶粒中的位错运动遇到晶界就会塞积下来 形不成宏观滑移,所以很难产生塑性形变。 但是,注意到式(1.23)指出:温度升高时,位错运动的速度加快,因此在相对较 高的温度下,脆性材料如Al2O等也可能发生一定程度的塑性形变。图1.12(a)示 出了在不同温度下测得的氧化铝单晶的应力应变关系曲线,可以看出:在温度不高 于1260℃的条件下,氧化铝单晶的形变基本表现为纯粹的弹性形变;而随着温度的 进一步升高,塑性形变则开始逐渐变得显著起来 201 断裂 1260℃(2300"F) 一上屈服应力 14 16 (a) (b) 12 下屈服应力 1270℃2318F -0.025 00 1370℃(2498F 0.002 -0.001 0.03038 伸长m 图1.12单晶氧化铝的形变行为 (a)祖度影响:(b》应变速率的影响 11b=453.6g:1in=2.54cm 由于滑移反映出来的宏观上的塑性形变是位错运动的结果,因此宏观测得的形 变速率也应该与位错运动有关,这一点可以借助 于图1.13所示的简化模型加以说明。 考虑如图1.13所示的一根长度为1的试件, 在外力作用下,在时间:内的总伸长量为△L。相 应地,试件的平均应变为c=兰,应变速率为= 图1.13塑性形变的简化模型