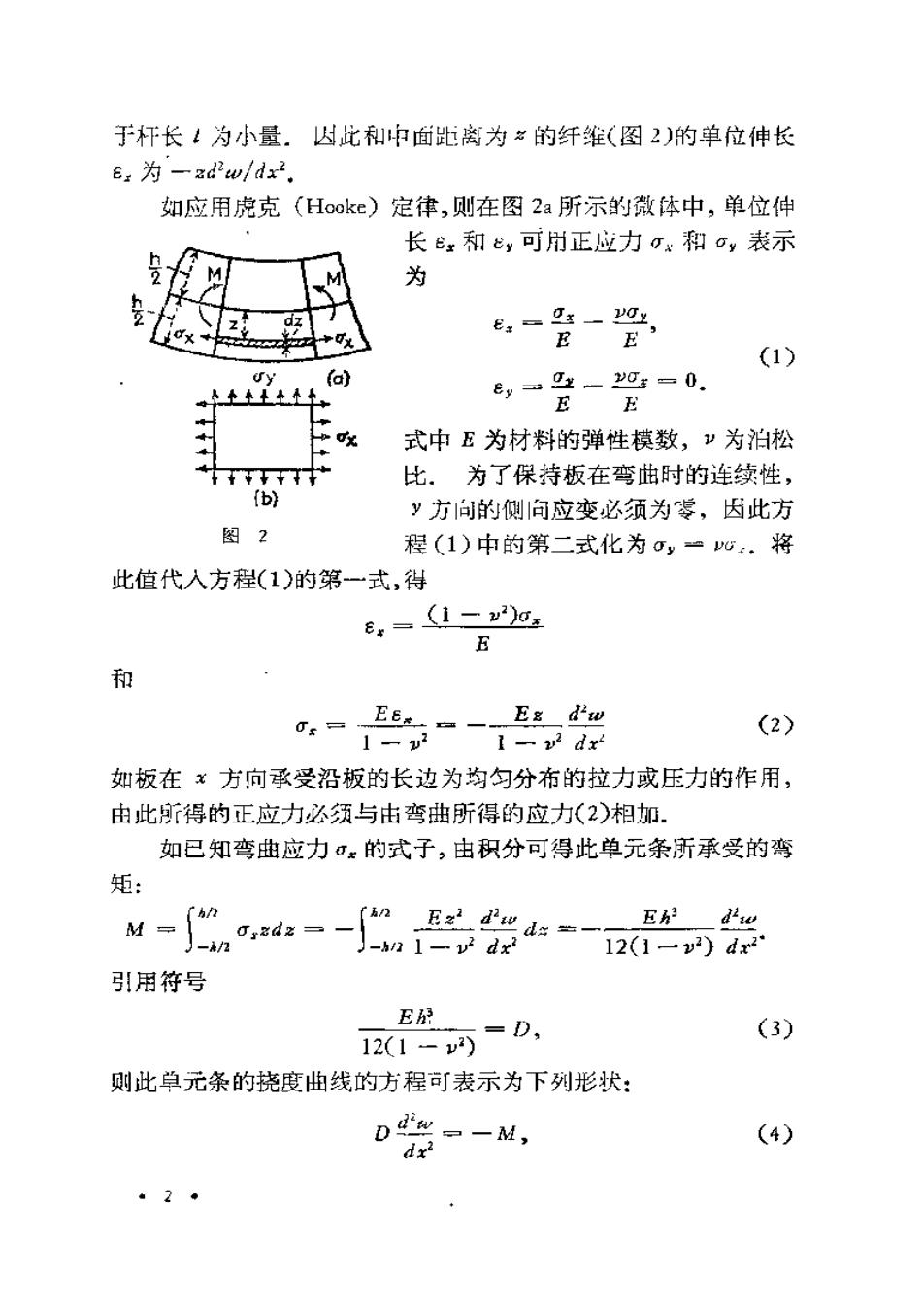
于干长1为小量.因比和中面离为名的纤维(图2)的单位伸长 ex为一zd2w/dx2. 如应用虎克(Hooke)定律,则在图2a所示的微体中,单位伸 长x和y可用正应力x和oy表示 为 e.=可-y0y E (1) (a) ey=2-cx-0, 式中E为材料的弹性模数,卫为泊松 比.为了保持板在弯曲时的连续性, (b) y方向的侧向应变必须为零,因此方 图2 程(1)中的第二式化为oy一心.将 此值代入方程(1)的第一式,得 6*=1一2a 和 Eg dw 0x= E6e一 (2) 1-w2 1-v2 dx 如板在方向承受沿板的长边为均匀分布的拉力或压力的作用, 由此所得的正应力必须与由弯曲所得的应力(2)相加. 如已知弯曲应力σ:的式子,由积分可得此单元条所承受的弯 矩 -a-n4 E dw 12(1一v2)dx2 引!用符号 E =D, (3) 12(1-y2) 则此卓元条的挠度曲线的方程表示为下列形状: D 曰一M, (4) 。2

式中D与粱弯曲问题中的F1相当,叫作板的弯曲刚度.这个方 程与梁的挠度微分方程具有同样形式.显然,板的挠度计算变成 了方程(4)的积分,如果作用在板上的只是侧向载荷,并且在挠度 出现时,棉对边能够自由绝彼此接近,则表示弯矩M的式子可以立 刻求得,从而挠度曲线叮由方(4)的积分得到.实际上.这个问题 是比饺复杂的,因为板往往与边界相连,其边缘不能自由移动.这 种支承方法将使板在发生挠度的同时,沿边缘产生拉伸反力.这 些反力随烧度的大小而变,并且影响方程(4)中的弯矩M.这问题 化成在侧问载荷和轴向力(其大小决定于此单元条的挠度)作用下 汽元条的曲的研究”.下面将对具有各种边界条件和承受均匀 载荷这种板的情祝讨沦此问题, 2,承受均匀载荷的简支矩形板的柱形弯曲 今讨论一承受 均匀载荷的长矩形板,被弯曲时其长边可自由旋转,但不能彼此 相问移动。由这板上截取一单元条,如图1所示,则得一承受均匀 载荷和轴向力S作用(图3)的杆,而S力的大小恰使杆的二端不 图3 能在x轴方向移动.用日表示均匀裁荷的强度,则此单元条在任 何横截面上的弯矩为 M-4xsw. 2 2 I)h.厂.y6HOB最先以这种形式讨论此问题:多看T'ren.Is.Naual Arch 第44卷,第15页,102年,和“Thcory of Structure of Ships”,第2卷,第 545页,¥彼得堡,914年,也可参看Stewart Way的论文,The National Meeting of Applied Mrchanics,A.S.M.F..New Haven,Conn.,1932 年6月:第2节和第3节所用的曲线即取自此论文。 3

代人方程(4),则得: w一5地=一92x+9x (a) 2D 2D 引用符号 s pu (5) D4 则方程(a)的通新可写成如形式: w= C,sinhC:cosh 842D gu'x gri (b) 842D 16u4D 积分常数G,与C,可由两端的条件决定、因为在此单元条两端的 挠殷为零,所以 当x=0和x=i时,w=0. (c) 将表示w的(b)式代入,则由以上二条件得到 C q.1一cosh2w 1644 )sinh 2u C294 16w4D1 而表示挠度w的(b)式化为: 94 (1-cosh 2u sinhu cosh ux1 16e4D sinh 2 +9x-x 8uD 8uD' 将下列式子 cosh 24 cosh sinhu,sinh 2 =2 sinh at cosh # cosh 1+sinh2 a 代入,则此式可化成较简单的形状: 2体x 2 sinh sinh coshcosh 16wD cosh u +92(1-x), 842D

或 oa0-分- (6) 16w4D 9x(-x). cosh t SuD 所以单元条的桡度随数最“而变,而由式(5)可闭的值又是轴向 力S的函数.力S可由单元条(图3)二端沿x轴方向不能移动这 个条件决定.所以轴向力S使单元条所产生的神长等于挠度曲线 的弧长与原长!的差.对于小挠度,这个差可由公式” (7) 表示 在计算单元条由力S所产生的伸长时,假定单元条在y方向 不可能有侧向应变。引用方程(2),即有 = 1-( (d) hE 将表示w的(6)式代人并进行积分,则得如下计算S的方程: S(1-2)l=9(5anh“+1tanh24 h它 D22567 256 +1 256 3849 由式(5)代人S=4D/2,由等式(3)代入D的表示式,最后可得 方程: E2h =135anh4+2辽tanh-35+9 (1一22g22816° (8) 168 16a8 d 若材料及比值/!和载荷9都已给定,则这方程的左边可以立刻 计算出来,而满足这方程的“值,可用试验校正法求得.则欲简化 这个解,可以采用图4所示的曲线:这些曲线的横坐标代表数值 4,纵坐标代表数值1ogo(10√U).符号U。表示方程(8)右端的 数值.采用√)。是因为它更容易由板的常数与载荷计算得到, 1)参看作者的“S1 rength ot Materials'”,第三版,第1卷,第178页,1955年, 5

在曲线4上u值是由B变到4 在曲线B上山值是由4变到8 在曲线C上u德是由8变到12 心家 4.0 10 35 曲线A 曲线C 曲线B 09 17 30 6 15 08 2.5 13 对u的数值 07 048 2610 37m 482 :的数值 4 064