南京大学：《电磁学》课程电子教案（教学课件）第九章 麦克斯韦方程与电磁波

圆电磁学09-03：电磁波的数学 A×(B×C) >激动人心的变换之二：磁场波动 =(4.C)B-(4.B)C .V×(V×H)=V(V.i)-Vi H=0=-V2i 如果初始电场 V×月=G E 或磁场取空间 波的形式，则 其一定会自发 .-VH=V× E Eo& 。(V×E) 在空间传播！ aH 17.E=0 :7×E=-W V×E=-4 a 2H,1/m2=(44)(8e)、1a27 at .VH=(4(88) 7.i=0 0 a I O'H V×H=6o6 =v2V2H u=1,8=1 in vacuum O'H =c2V2H 812 812

电磁学09-03: 电磁波的数学  激动人心的变换之二：磁场波动 2 2 2 0 0 2 0 0 2 0 00 2 2 0 0 2 0 0 0 1/ ( )( ( )( ) ( ) ( ) , ( )( ) ( )( ) H v H HH H E E H H t t E H E t t H H E H t tt H H t                                                                                                 2 2 2 2 2 2 2 2 2 2 2 1, 1 in vacuum ) 1 H H v H H c H t v t t                       ( ) ( )( ) A BC A CB A BC             如果初始电场 或磁场取空间 波的形式，则 其一定会自发 在空间传播！ 0 0 0 0 E H E t H E H t                            

厦电磁学09.03：电磁波的数学 口电磁波作为波动（平面波）行为的性质： E=Ecos(ot-k-F) a"H H=Hocos(@tk+) →2=0 8t2 =VH 2 元，0=2πf→v=f 1/v2=(4)(E8)=Cem > 计算所得Cm“碰巧”与光束相同→光是电磁波的第一个证据。 >介质中电磁波速率与(8，四相关

电磁学09-03: 电磁波的数学  电磁波作为波动(平面波)行为的性质： 2 2 2 2 2 2 2 2 2 2 2 0 0 0 2 0 0 0 cos( ) cos( ) 2 , 2 1/ ( )( ) 1 em E E t kr H H t kr E v E t k H v v H t k fv c f v                                                     计算所得 cem “碰巧”与光束相同  光是电磁波的第一个证据。  介质中电磁波速率与 ( , ) 相关

电磁学09.03：电磁波的数学 ▣电磁波是横波： E=Ecos(@t-k-F) 7.E=0 H-Hocos(@t-k+) V.i=0 (k,Eox+k Eoy +k.Eoz)sin(ct-kF)=0 [尼。=0K1。 (k,Hos +kyHoy+k.Ho)sin(tk+)=0 i。=01i。 口电场与磁场垂直： E=E cos(@t-kF) 三7×E=-44 aH i=i。cos(ot-k:f+p) 8t K⊥E。 k×E。sin(ot-k.f)=uHsin(ot-k,f+p)→.∴ k⊥i。 ot-K.f=ot-k.F+0K1。 E。上i。 0=0 K×E。=4oH。 k⊥H

电磁学09-03: 电磁波的数学  电磁波是横波： 000 0 0 000 0 0 0 0 cos( ) cos( ) 0 0 ( )sin 0 ( )si ( )0 n( ) 0 0 xx yy zz xx yy zz E E t kr H H t kr E H kE kE kE kE k E kH kH kH k H k H t kr t kr                                                                     电场与磁场垂直： 0 0 0 0 0 0 0 00 0 00 0 0 0 cos( ) cos( ) sin( ) sin( ) , 0 E E t kr H E H H t kr t k E t kr H t kr t kr t kr k E kE H k k E k E H H H                                                                                                         

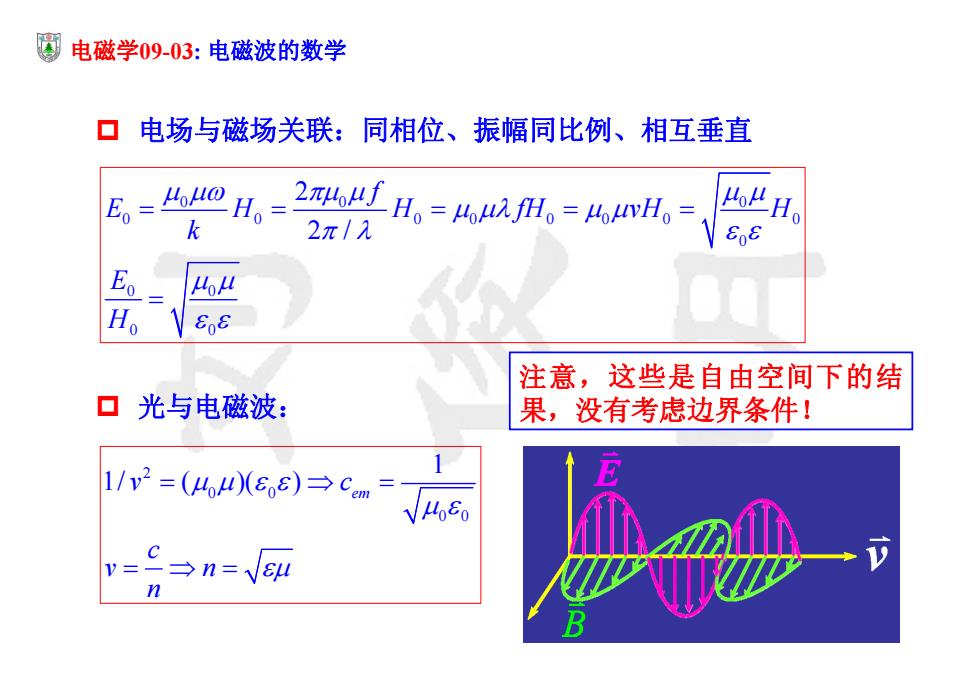
电磁学09-03：电磁波的数学 口电场与磁场关联：同相位、振幅同比例、相互垂直 E=0 244fH。=4,H=4wH 4H 2π/1 Eo o Ho 注意，这些是自由空间下的结 ▣光与电磁波： 果，没有考虑边界条件！ 1/v2=(40(88)→Cem 0 v=→n=V C n

电磁学09-03: 电磁波的数学  电场与磁场关联：同相位、振幅同比例、相互垂直 00 0 0 0 00 00 0 0 0 0 0 0 0 2 2 / f EH H fH vH H k E H                        光与电磁波： 2 0 0 0 0 1 1/ ( )( ) em v c c v n n         注意，这些是自由空间下的结 果，没有考虑边界条件！

电磁学09-03：电磁波的数学 口电磁波卡通 Z electromagnetic wave electromagnetic wave di

电磁学09-03: 电磁波的数学  电磁波卡通